- 2021-10-27 发布 |
- 37.5 KB |
- 2页

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上册青岛版数学教案5-6几何证明举例
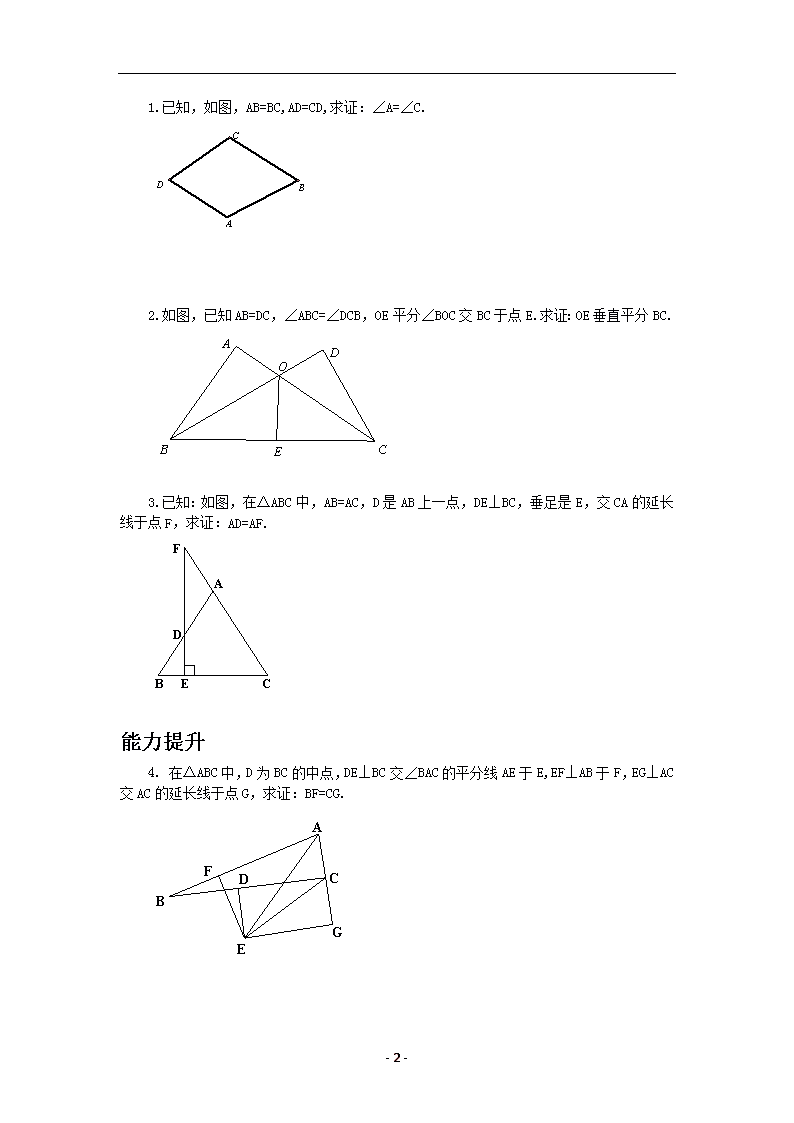
- 1 - 5.6 几何证明举例 学习目标 1.熟练掌握 AAS,HL 判定定理,等腰三角形,等边三角形性质与判定定理,并会运用这些定 理进行证明相关题目; 2.通过独立思考,合作探究,探究出综合法证明几何问题的方法。 3.全力以赴,达成目标,享受几何证明的多样性之美。 自主探究 (一) 直角三角形全等的判定定理 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对 应相等,那么这两个直角三角形全等。(HL 定理) 【典型例题】 D F E B C A 例 1.已知如图,D 是△ABC 的边 BC 的中点,DE⊥AC,DF⊥AB,垂足分别是点 E,F,DE=DF. 求证:△ABC 是等腰三角形. (二)等腰三角形的性质和判定 命题一:等腰三角形底边上的高、中线及顶角的平分线重合. 已知: 求证: 证明: 命题二:有两个角相等的三角形是等腰三角形. 已知: 求证: 证明: (三)角平分线与垂直平分线的性质与判定 三角形全等的运用 1.已知,如图,AB=BC,AD=CD,求证:∠A=∠C. - 2 - C B A D 2.如图,已知 AB=DC,∠ABC=∠DCB,OE 平分∠BOC 交 BC 于点 E.求证:OE 垂直平分 BC. O D C E B A 3.已知:如图,在△ABC 中,AB=AC,D 是 AB 上一点,DE⊥BC,垂足是 E,交 CA 的延长 线于点 F,求证:AD=AF.� F � E � D � C � B � A 能力提升 4. 在△ABC 中,D 为 BC 的中点,DE⊥BC 交∠BAC 的平分线 AE 于 E,EF⊥AB 于 F,EG⊥ AC 交 AC 的延长线于点 G,求证:BF=CG. � G � F � E � D � C � B � A查看更多