2020-2021学年人教版初二数学上学期期中考测试卷01
2020-2021学年人教版初二数学上学期期中考测试卷01
一. 选择题(共12小题)
1.(2020·西藏日喀则期末)一个等腰三角形的两边长分别为4厘米、9厘米,则这个三角形的周长为( )
A.17或22 B.22 C.13 D.17或13
【答案】B
【解析】
解:分类讨论:
情况一:若4厘米为腰长,9厘米为底边长,
由于4+4<9,则三角形不存在;
情况二:若9厘米为腰长,则符合三角形的两边之和大于第三边.
所以这个三角形的周长为9+9+4=22(厘米).
故选:B.
2.(2020·河南遂平期末)已知是的三边长,其中是二元一次方程组的解,那么的值可能是下面四个数中的( )
A.2 B.6 C.10 D.18
【答案】B
【解析】
解:由题意可知:,
(2)-(1)式得:
a=6,代回(1)中,解得b=4,
根据三角形两边之和大于第三边,两边之差小于第三边可知,
6-4
”“<”或“=”);
(2)若的周长比的周长多4,且,求AB,AC的长;
(3)的周长为27,,BC边上的中线,的周长为19,求AC
的长.
【答案】(1);(2);(3)8.
【解析】
(1)为BC边上的中线,
,
与等底同高,
,
故答案为:;
(2)∵AD是BC边上的中线,
,
的周长比的周长多4,即,
,
又,
;
(3)的周长为27,,
,即,
解得,
,
又的周长为19,,
,即,
解得.
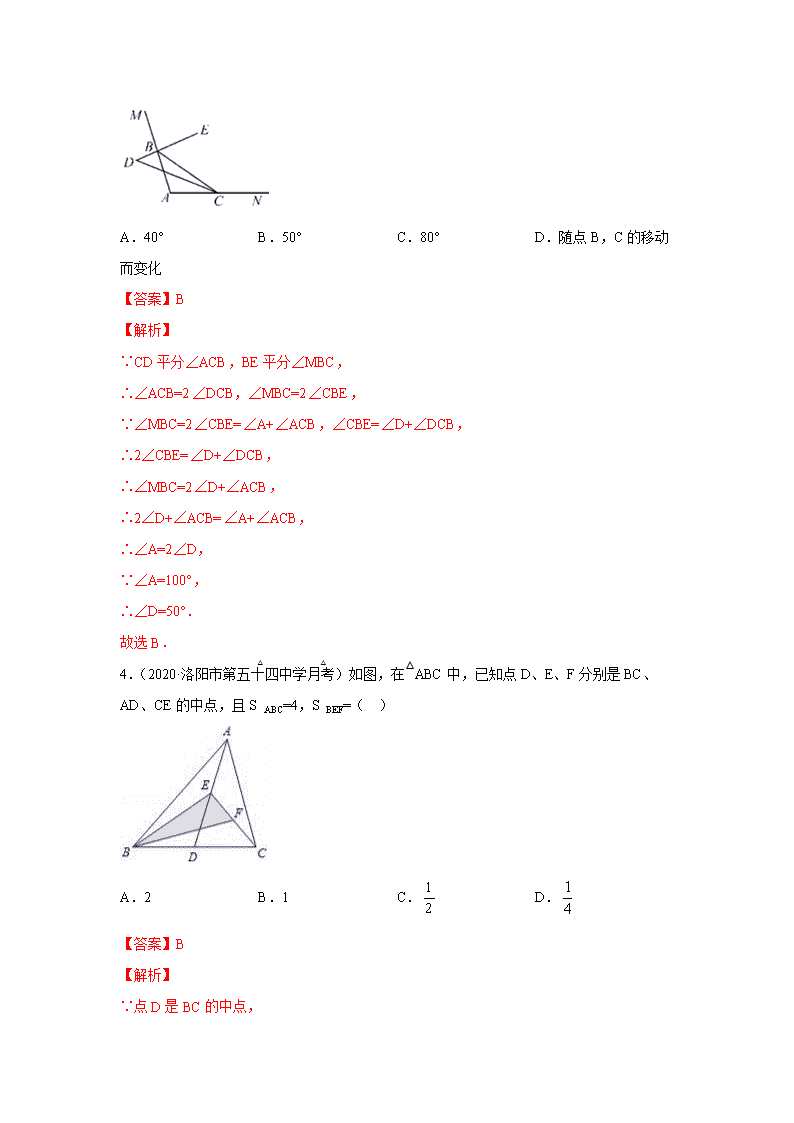
20.(2020·山东单县期末)如图,在中,平分为线段上的点,交直线于点
若,求的度数;
试说明:
【答案】(1)25°;(2)证明见解析
【解析】
解:(1)因为∠B=35°,∠ACB=85°
所以∠BAC=180°-∠B-∠ACB=60°
因为AD平分∠BAC
所以∠BAD=∠BAC=30°
所以∠ADC=∠B+∠BAD=65°
又因为PE⊥AD
所以∠ADC与∠E互余
所以∠E=90°-65°=25°
(2)因为AD平分∠BAC
所以∠BAD=∠BAC
所以∠ADC=∠B+∠BAD
=∠B+∠BAC
=∠B+(180°-∠B-∠ACB)
=90°+∠B-∠ACB
因为PE⊥AD
所以∠E=90°-∠ADC
=90°-(90°+∠B-∠ACB)
=(∠ACB-∠B)
21.(2020·昌乐县北大公学双语学校月考)如图,四边形ABCD中,对角线AC、BD交于点O,AB=AC,点E是BD上一点,且AE=AD,∠EAD=∠BAC.
(1)求证:∠ABD=∠ACD;
(2)若∠ACB=62°,求∠BDC的度数.
【答案】(1)详见解析;(2)56°
【解析】
证明:(1)∵∠EAD=∠BAC
∴∠BAE=∠CAD,且AB=AC,AD=AE,
∴△ABE≌△ACD(SAS)
∴∠ABD=∠ACD
(2)∵AB=AC,∠ACB=62°
∴∠ABC=∠ACB=62°,
∴∠BAC=180°-62°-62°=56°
∵∠BAO+∠ABO+∠AOB=180°,∠DCA+∠DOC+∠BDC=180°
∴∠BAC=∠BDC=56°
22.(2020·河南太康期末)如图,∠ADE+∠BCF=180°,AF平分∠BAD,∠BAD=2∠F.
(1)AD与BC平行吗?请说明理由.
(2)AB与EF的位置关系如何?为什么?
(3)若BE平分∠ABC.试说明:①∠ABC=2∠E;②∠E+∠F=90°.
【解析】
解:(1),理由如下:
,,
,
.
(2),理由如下:
平分,,
,
.
(3)①,理由如下:
,
.
平分,
.
②,理由如下:
,
.
,,
,
.
23.(2020·广东南海石门中学一模)如图,与为正三角形,,,三点在一条直线上,与交于点,.
(1)求证:;
(2)求证:.
【解析】
证明:(1)与为正三角形,
,,,
,
;
(2),
,,
为正三角形,
,
,
,
,
,
,
.
24.(2020·山东中区期末)如图,在中,已知,的垂直平分线交于点,交于点,连接
(1)若,则的度数是 度
(2)若,的周长是
①求的长度;
②若点为直线上一点,请你直接写出周长的最小值
【答案】(1)40°;(2)①8;②
【解析】
【分析】
(1)根据垂直平分线上的点到线段两个端点距离相等得,再根据等腰三角形的性质即可求解;
(2)①根据垂直平分线的性质得,的周长是,,即可求的长度;
②当点与点重合时,周长的最小,即为的周长.
【详解】
解:(1),
,
,
,
是的垂直平分线,
,
,
,
,
.
故答案为.
(2)①,
的周长是,
即
,
,
,
.
答:的长度为.
②点B关于MN对称点为A,AC与MN交于点M,
∴当点与点重合时,周长的值最小,且为AC+BC=10+8=18cm,
∴的周长的最小值为.