- 2021-10-27 发布 |
- 37.5 KB |
- 27页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
八年级上数学课件八年级上册数学课件《一次函数的应用》 北师大版 (8)_北师大版
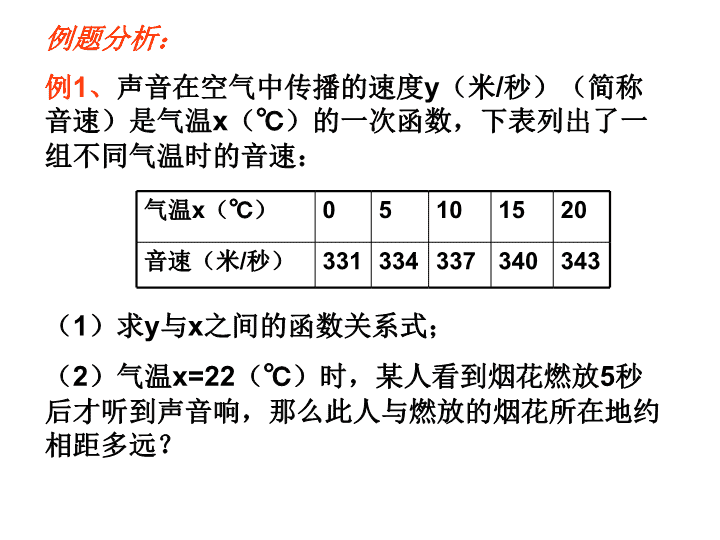
一次函数的应用 基础训练: 1、某地市区打电话的收费标准为:3分钟以内(含 3分钟)收费0.2元,超过分钟,每增加1分钟(不足1分 钟,按1分钟计算)加收0.11元,那么当时间超过3分钟 时,求:电话费y(元)与时间t(分)之间的函数关系式. 2、为了加强公民的节水意识,某市制定了如下的用 水收费标准:每户每月的用水不超过10吨时,水价为 每吨1.2元;超过10吨时,超过的部分按每吨1.8元收费, 该市某户居民5月份用水x吨(x>10),应交水费y元,求y 与x之间的函数关系式. 例题分析: 例1、声音在空气中传播的速度y(米/秒)(简称 音速)是气温x(℃)的一次函数,下表列出了 一组不同气温时的音速: 气温x(℃) 0 5 10 15 20 音速(米/秒) 331 334 337 340 343 (1)求y与x之间的函数关系式; (2)气温x=22(℃)时,某人看到烟花燃放5秒 后才听到声音响,那么此人与燃放的烟花所在地约 相距多远? 若点(1,2)及(m,3)都在正比例 函数y=kx的图象上,求m的值。 已知直线y=kx+b经过点(-2,-1) 和点(2,-3),求这条直线的函数 解析式。 某一次函数的图象平行于直线 ,且过点(4,7),求函数 解析式。 xy 2 1 例1 去年入夏以来,全国大部分地区发生严重 干旱,某市自来水公司为了鼓励市民节约用水, 采取分段收费标准,若某居民每月应交水费是 用水量的函数,其函数图象如图所示: (1)分别写出x≤5和x>5时,y与x的函数解析式; (2)观察函数图象,利用函数解析式,回答自来水 公司采取的收费标准。 (3)若某户居民该月用水3.5 吨,则应交水费多少元? 若该月交水费9元,则用水 多少吨? xO y 5 8 3.6 6.3 例3、甲乙两家体育用品商店出售同样的乒乓球 拍和乒乓球,乒乓球拍每付定价20元,乒乓球 每盒5元,现两家商店搞促销活动,甲店:每买 一付球拍赠一盒乒乓球;乙店:按定价的9折优 惠,某班级需要购球拍4付,乒乓球若干盒(不 少于4盒)。 (1)、设购买乒乓球盒数为x(盒),在甲店 购买的付款数为y甲(元),在乙店购买的付款 数为y乙(元),分别写出在两家商店购买的付 款数与乒乓球盒数x之间的函数关系式。 (2)就乒乓球盒数讨论去哪家商店购买合算? 例4、某图书馆开展两种方式的租书业务:一种 是使用会员卡,另一种是使用租书卡。使用这 两种卡租书,租书金额y(元)与租书时间x (天)之间的关系如图所示。 (1)分别写出用租书卡和会员卡租书的金额y(元) 与租书时间x(天)之间的函数关系式; (2)两种租书方式每天租书的收费分别是多少元? (3)若两种租书卡的使用 期限均为一年,则在这一年 中如何选择这两种租书方式 比较合算? x100 20 50 o y(元) (天) 租书卡 会员卡 例6 预防“非典”期间,某种消毒液A市需 要6吨,B市需要8吨,正好M市储备有10吨, N市储备有4吨,预防“非典”领导小组决定 将这14吨消毒液调往A市和B市,消毒液的运 费价格如下表。设从M市调运x吨到A市。 (1)求调运14吨消毒液的总运费y关于x的 函数关系式; (2)求出总运费最低的调运方案,最低运 费的多少? 终 点起点 A B M 60 100 N 35 70 回味练习: 1、函数y=2x图象经过点(0, )与点 (1, ),y随x的增大而 ; 2、函数y=(a-2)x的图象经过第二、 四象限,则a的范围是 ; 3、函数y=(1-k)x中y随x的增大而减 小,则k的范围是 . 0 2 增大 a<2 k>1 4、直线y=-3x-6与x轴的交点坐标 是 ,与y轴的交点坐标 为 . 5、直线y=3x-1经过 象限 直线y=-2x+5经过 象限 一、三、四 一、二、四 (-2,0) (0,-6) 6、直线y=kx+b(k<0,b<0)经过 象限。 7、若直线y=kx+b经过一、二、四象限, 则k 0,b 0. 8、直线y=kx+b的图象如图所示,确定k、 b符号: 二、三、四 < > o y x o y x K<0,b>0 k>0,b<0 9、已知一次函数y=(m-1)x+2m+1 (1)若图象经过原点,求m的值; (2)若图象平行于直线y=2x,求m的值; (3)若图象交y轴 于正半轴,求m的取值范围; (4)若图象经过一、二、四象限,求m的取值范 围。 (5)若图象不过第三象限,求m的取值范围。 (6)若随的增大而增大,求m的取值范围。 axy 2 bxy 10、已知一次函数 与 的图像都经过A(-2,0), 且与轴分别交于B、C两点,求△ABC 的面积 11、若直线y=3x+b与两坐标轴 所围成的三角形的面积为6, 求b的值。 12、无论m为何值,直线y=x+2m 与y=-x+4的交点不可能在( ) A、第一象限 B、第二象限 C、第三象限 D、第四象限 13、已知y=y1+y2,其中y1与x成正比例, y2与(x-2)成正比例,又当x=-1时, y=2;当x=2时,y=5. 求y与x的函数 关系式。 例 为了迎接2002年世界杯足球赛的到来,某足球 协会举办了一次足球联赛,其记分规则及奖励方 案如下表: 比赛进行到第12轮(每队均比赛12场)A队积19分 (1)请通过计算,判断A队胜、平、负各几场 (2)若每赛一场,每名参赛队员均得出场费500元, 设A队其中一名参赛队员所得的奖金与出场费的和 为W(元),试求W的最大值 胜一场 平一场 负一场 积 分 3 1 0 奖金(元/人) 1500 700 0 例、已知A、B两地相距300千米,现有甲、乙两车 同时从A地开往B地,甲车匀速行驶2小时到达AB 中点C地,停留2小时后,再匀速行驶1.5小时到 达B地;乙车以每小时v千米(v≠75)的速度行驶 (1)设s (千米)、t (小时)分别表示甲车离开A地 的路程和时间,试在下列条件下: ①0≤t≤2 ②2查看更多
相关文章
- 当前文档收益归属上传用户