- 2021-10-26 发布 |
- 37.5 KB |
- 7页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学华东师大版八年级上册教案15-2 第2课时 统计图的选择
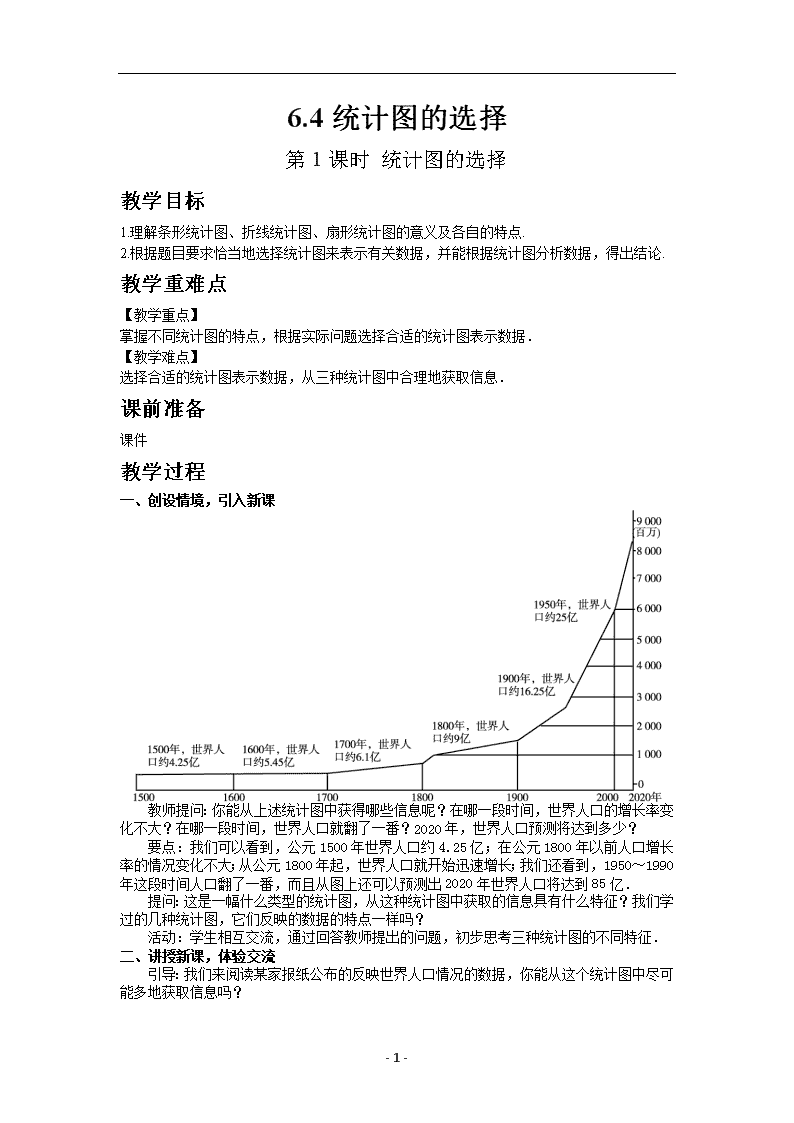
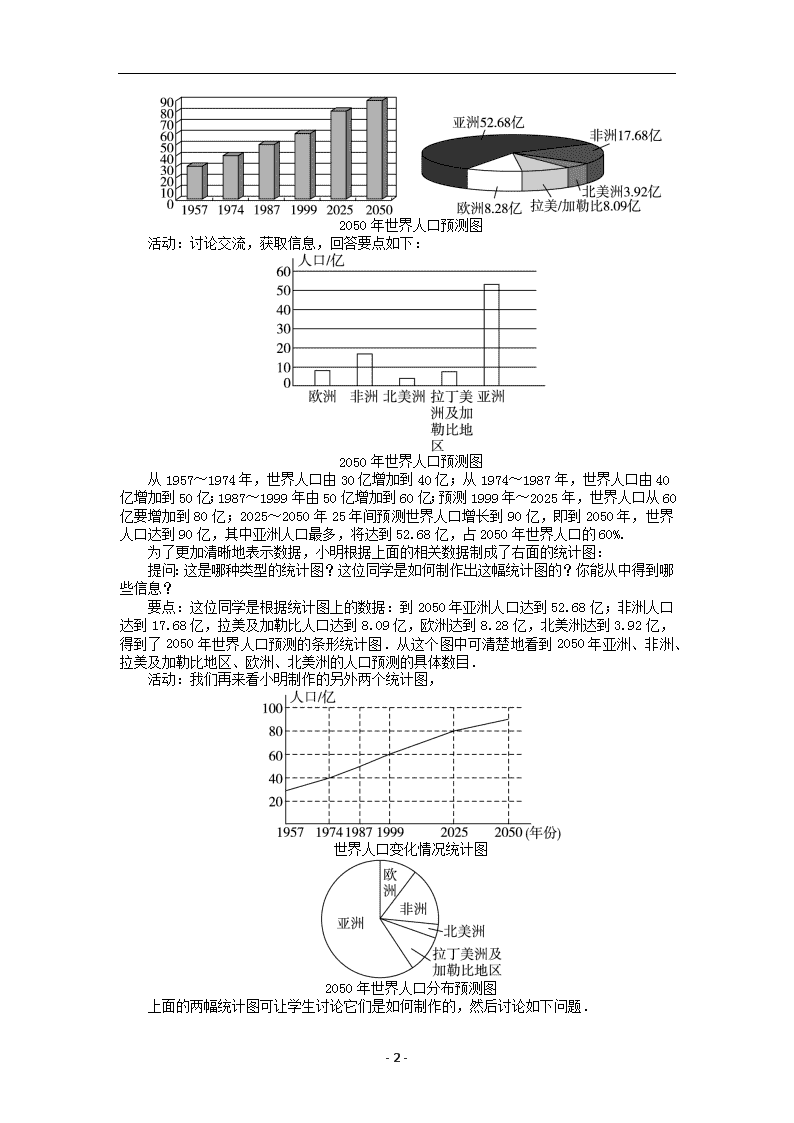
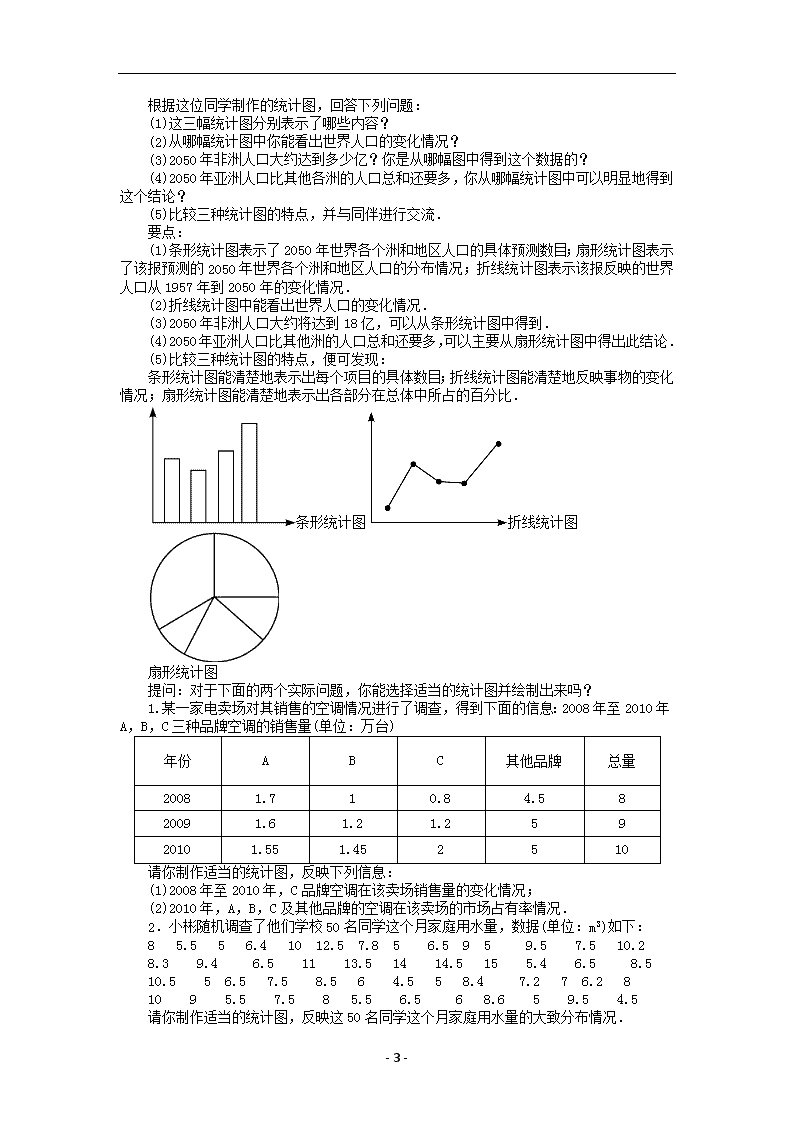
- 1 - 6.4 统计图的选择 第 1课时 统计图的选择 教学目标 1.理解条形统计图、折线统计图、扇形统计图的意义及各自的特点. 2.根据题目要求恰当地选择统计图来表示有关数据,并能根据统计图分析数据,得出结论. 教学重难点 【教学重点】 掌握不同统计图的特点,根据实际问题选择合适的统计图表示数据. 【教学难点】 选择合适的统计图表示数据,从三种统计图中合理地获取信息. 课前准备 课件 教学过程 一、创设情境,引入新课 教师提问:你能从上述统计图中获得哪些信息呢?在哪一段时间,世界人口的增长率变 化不大?在哪一段时间,世界人口就翻了一番?2020 年,世界人口预测将达到多少? 要点:我们可以看到,公元 1500 年世界人口约 4.25 亿;在公元 1800 年以前人口增长 率的情况变化不大;从公元 1800 年起,世界人口就开始迅速增长;我们还看到,1950~1990 年这段时间人口翻了一番,而且从图上还可以预测出 2020 年世界人口将达到 85 亿. 提问:这是一幅什么类型的统计图,从这种统计图中获取的信息具有什么特征?我们学 过的几种统计图,它们反映的数据的特点一样吗? 活动:学生相互交流,通过回答教师提出的问题,初步思考三种统计图的不同特征. 二、讲授新课,体验交流 引导:我们来阅读某家报纸公布的反映世界人口情况的数据,你能从这个统计图中尽可 能多地获取信息吗? - 2 - 2050 年世界人口预测图 活动:讨论交流,获取信息,回答要点如下: 2050 年世界人口预测图 从 1957~1974 年,世界人口由 30 亿增加到 40 亿;从 1974~1987 年,世界人口由 40 亿增加到 50 亿;1987~1999 年由 50 亿增加到 60 亿;预测 1999 年~2025 年,世界人口从 60 亿要增加到 80 亿;2025~2050 年 25 年间预测世界人口增长到 90 亿,即到 2050 年,世 界人口达到 90 亿,其中亚洲人口最多,将达到 52.68 亿,占 2050 年世界人口的 60%. 为了更加清晰地表示数据,小明根据上面的相关数据制成了右面的统计图: 提问:这是哪种类型的统计图?这位同学是如何制作出这幅统计图的?你能从中得到哪 些信息? 要点:这位同学是根据统计图上的数据:到 2050 年亚洲人口达到 52.68 亿;非洲人口 达到 17.68 亿,拉美及加勒比人口达到 8.09 亿,欧洲达到 8.28 亿,北美洲达到 3.92 亿, 得到了 2050 年世界人口预测的条形统计图.从这个图中可清楚地看到 2050 年亚洲、非洲、 拉美及加勒比地区、欧洲、北美洲的人口预测的具体数目. 活动:我们再来看小明制作的另外两个统计图, 世界人口变化情况统计图 2050 年世界人口分布预测图 上面的两幅统计图可让学生讨论它们是如何制作的,然后讨论如下问题. - 3 - 根据这位同学制作的统计图,回答下列问题: (1)这三幅统计图分别表示了哪些内容? (2)从哪幅统计图中你能看出世界人口的变化情况? (3)2050 年非洲人口大约达到多少亿?你是从哪幅图中得到这个数据的? (4)2050 年亚洲人口比其他各洲的人口总和还要多,你从哪幅统计图中可以明显地得到 这个结论? (5)比较三种统计图的特点,并与同伴进行交流. 要点: (1)条形统计图表示了 2050 年世界各个洲和地区人口的具体预测数目;扇形统计图表示 了该报预测的 2050 年世界各个洲和地区人口的分布情况;折线统计图表示该报反映的世界 人口从 1957 年到 2050 年的变化情况. (2)折线统计图中能看出世界人口的变化情况. (3)2050 年非洲人口大约将达到 18 亿,可以从条形统计图中得到. (4)2050 年亚洲人口比其他洲的人口总和还要多,可以主要从扇形统计图中得出此结论. (5)比较三种统计图的特点,便可发现: 条形统计图能清楚地表示出每个项目的具体数目;折线统计图能清楚地反映事物的变化 情况;扇形统计图能清楚地表示出各部分在总体中所占的百分比. 条形统计图 折线统计图 扇形统计图 提问:对于下面的两个实际问题,你能选择适当的统计图并绘制出来吗? 1.某一家电卖场对其销售的空调情况进行了调查,得到下面的信息:2008 年至 2010 年 A,B,C 三种品牌空调的销售量(单位:万台) 年份 A B C 其他品牌 总量 2008 1.7 1 0.8 4.5 8 2009 1.6 1.2 1.2 5 9 2010 1.55 1.45 2 5 10 请你制作适当的统计图,反映下列信息: (1)2008 年至 2010 年,C品牌空调在该卖场销售量的变化情况; (2)2010 年,A,B,C 及其他品牌的空调在该卖场的市场占有率情况. 2.小彬随机调查了他们学校 50 名同学这个月家庭用水量,数据(单位:m 3 )如下: 8 5.5 5 6.4 10 12.5 7.8 5 6.5 9 5 9.5 7.5 10.2 8.3 9.4 6.5 11 13.5 14 14.5 15 5.4 6.5 8.5 10.5 5 6.5 7.5 8.5 6 4.5 5 8.4 7.2 7 6.2 8 10 9 5.5 7.5 8 5.5 6.5 6 8.6 5 9.5 4.5 请你制作适当的统计图,反映这 50 名同学这个月家庭用水量的大致分布情况. - 4 - 活动:讨论交流,根据所获取的信息制作适当的统计图,参考答案如下: 1. 某家电卖场 2008 年至 2010 年 C 品牌空调销售量变化统计图 (1) 2010 年 A,B,C及其他品牌空调在某家电卖场的市场占有率统计图 (2) 2. 说明:这里的 4~6 表示大于等于 4 且小于 6,其他类似. 三、拓展创新、巩固新知 探究点一:统计图的选择 要反映某市一周大气中 PM2.5的含量变化情况,宜采用() A.条形统计图 B.折线统计图 D.扇形统计图 D.频数直方图 解析:因为 PM2.5的含量变化没有规律,只能测出不同变化情况,应选折线统计图, 故选 B. 方法总结:要结合三种统计图的缺点进行选择,条形统计图不能反映各部分在总体中的 百分比;折线统计图除了不能反映各部分在总体中的百分比外,还不能反映每一部分的具体 数量;扇形统计图也不能反映各部分的具体数量. 探究点二:统计图的转换 某中学七年级(1)班共有学生 40 人,该班开设了排球、篮球和足球三项体育 兴趣课,要求每个学生必须参加,且只能参加其中一项球类运动.图①是小明同学把该班学 生报名统计后,绘制成条形统计图的一部分. - 5 - (1)请你帮小明同学把条形统计图补充完整; (2)请你根据条形统计图中的数据,改用扇形统计图表示出来(如图②); (3)从统计图中你可以获得哪些信息?(写出一条) 解析:(1)先求出参加排球兴趣课的人数,进而可补充条形统计图;(2)从条形统计图 得出各种兴趣课人数,用它们分别除以 40,即可求出相应的百分比,进而可求出相应扇形 圆心角度数,画出扇形统计图;(3)答案不唯一,只要合理即可. 解:(1)参加排球活动的有 40-20-12=8(人),补充图形如图③所示; (2)从条形统计图可知,参加足球活动的有 20人,占总人数的百分比为 20÷40×100% =50%,圆心角的度数为 360°×50%=180°;参加排球活动的有 8人,占总人数的百分比为 8÷40×100%=20%,圆心角的度数为 360°×20%=72°;参加篮球活动的有 12人,占总人 数的百分比为 12÷40×100%=30%,圆心角的度数为 360°×30%=108°,扇形统计图如图④ 所示; (3)答案不唯一,如:该班参加足球活动人数是参加排球活动人数与参加篮球活动人 数之和;参加足球活动人数是参加排球活动人数的 2.5倍等. 方法总结:三种统计图的画法:(1)条形统计图:①画坐标;②确定单位长度;③标出 高度,作出条形;(2)折线统计图:①画坐标;②确定单位长度;③描点;④连线(线段); (3)扇形统计图:①计算出总体;②算出各部分百分比;③计算各扇形的圆心角度数;④ 画扇形,在各部分标明名称、百分比. 探究点三:统计图的误导 如图所示是 2010 年~2014年甲、乙两个公司产品销售情况统计图.由统计图可 知,销量增速较快的公司是( ) A.甲公司 B.乙公司 C.一样快 D.无法确定 解析:若横坐标被“压缩”,纵坐标被“放大”,则给人造成统计量的变化速度加快的错 - 6 - 觉,反之,就会给人造成统计量的变化速度减慢的错觉.本题两个公司的增速一样快,故选 C. 方法总结:绘制折线统计图时要注意坐标轴单位长度所表示的量,不要造成直观产生的 错觉. 探究点四:综合利用不同的统计图中的信息 某校为了调查学生视力变化情况,从该校 2013年入校的学生中抽取了部分学生 进行连续三年的视力跟踪调查,将所得数据处理,制成折线统计图和扇形统计图,如图所示: (1)该校被抽查的学生共有多少名? (2)现规定视力 5.1及以上为合格,若被抽查年级共有 600名学生,估计该年级在 2015 年有多少名学生视力合格. 解析:由折线统计图可知 2015年被抽取的学生人数,且扇形统计图中对应的 A 区所占 的百分比已知,由此即可求出被抽查的学生人数;根据扇形统计图中 C、D 区所占的百分比, 即可求出该年级在 2015年有多少名学生视力合格. 解:(1)该校被抽查的学生人数为 80÷40%=200(人); (2)估计该年级在 2015年视力合格的学生人数为 600×(10%+20%)=180(人). 方法总结:本题的解题技巧在于从两个统计图中获取正确的信息,并互相补充互相利用. 例如求被抽查的学生人数时,由折线统计图可知 2015年被抽取的学生人数是 80人,与其相 对应的是扇形统计图中的 A 区,而 A 区所占的百分比是 40%,由此求出被抽查的学生人数 为 80÷40%=200(人). 四、随堂练习,加强认识 2008 年 5 月 12 日,我国四川汶川发生了里氏 8.0 级的地震,全国各地纷纷捐款捐物支 援灾区.从四川省人民政府每天下午 5点举行的新闻发布会上,得到如下信息: 四川省财政收到的抗震救灾专项资金/亿元 四川省财政共向灾 区调拨救灾应急资 金/亿元中央财政下达救灾 专项资金 各类捐款 合计 截至 5 月 18 日 17.73 9.13 26.86 23.97 截至 5 月 22 日 35.83 10.99 46.82 56.02 截至 5 月 26 日 41.83 17.08 58.91 57.5 请你制作适当的统计图,反映下列信息: (1)截至 5 月 18 日、5 月 22 日、5 月 26 日,四川省财政收到的抗震救灾专项资金的总 数情况; (2)截至 5 月 18 日、5 月 22 日、5 月 26 日,四川省财政共向灾区调拨救灾应急资金的 变化情况; - 7 - (3)截至 5 月 22 日,中央财政下达救灾专项资金和各类捐款在四川省财政收到的专项资 金中的比例情况. 解:(1)条形统计图 截至 5 月 18 日、22 日、26 日四川财政 收到的抗震救灾专项资金总数统计图 (2)折线统计图 截至 5 月 18 日、22 日、26 日四川财政向灾区 调拨救灾应急资金变化情况统计图 (3)扇形统计图 截至 5 月 22 日中央财政下达救灾专项资金和各类 捐款在四川财政收到的专项资金中的比例统计图 五、归纳小结,反思提高 三种统计图表示数据的特点,折线统计图一定表示同一对象的发展趋势,不同对象是不 能利用折线统计图的;涉及具体数目的一般利用条形统计图;有具体数目但主要关注比例时 利用扇形统计图. 六、评价与反思 教学过程中,应鼓励学生积极参与教学活动,在活动中,体会数学的实用性,从而产生 对数学的好奇心和求知欲. 七、板书设计 统计图 的选择 条形统计图→清楚地表示每个项目的具体数目 折线统计图→清楚地反映事物的变化情况 扇形统计图→ 清楚地表示出各个部分在总体中 所占的百分比查看更多