湖南省长沙市明达中学2021届九年级上学期第一次月考数学试题

湖南省长沙市明达中学2021届九年级上学期第一次月考数学试题

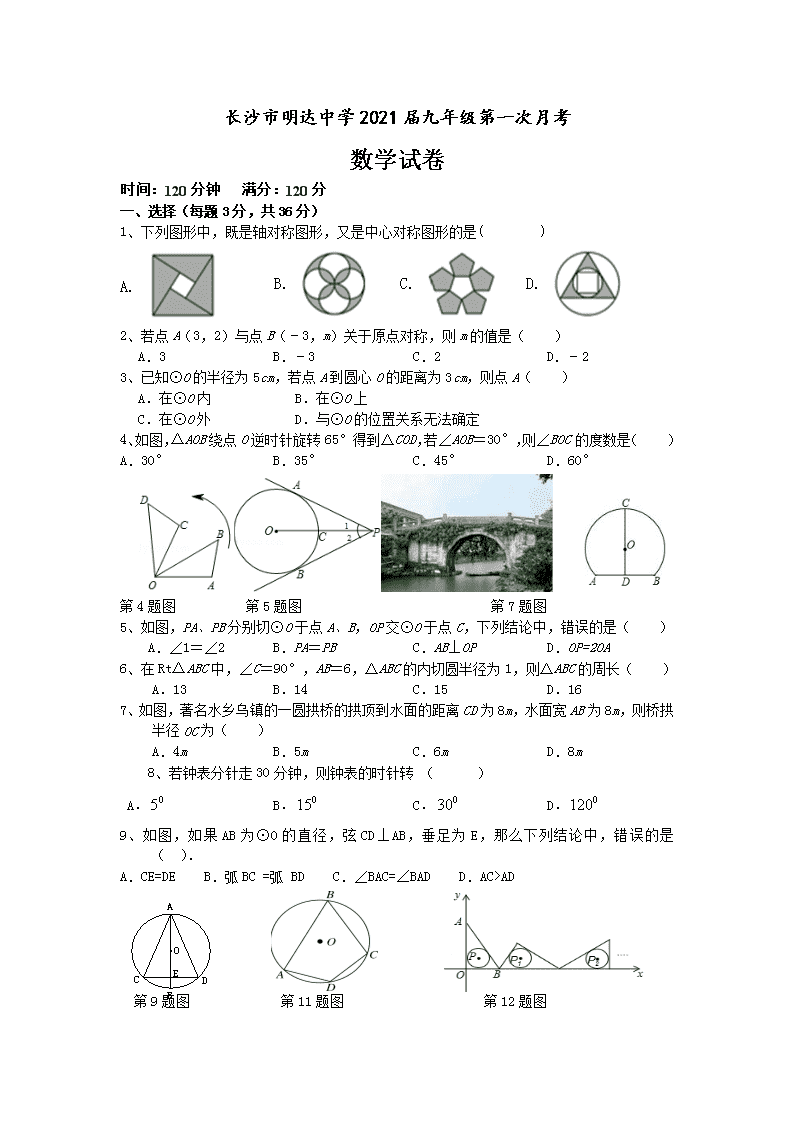
长沙市明达中学2021届九年级第一次月考 数学试卷 时间：120分钟 满分：120分 ‎ 一、选择（每题3分，共36分）‎ ‎1、下列图形中，既是轴对称图形，又是中心对称图形的是( )‎ A. ‎ B. C. D. ‎ ‎2、若点A（3，2）与点B（﹣3，m）关于原点对称，则m的值是（　　）‎ A．3 B．﹣‎3 ‎C．2 D．﹣2‎ ‎3、已知⊙O的半径为‎5cm，若点A到圆心O的距离为‎3cm，则点A（　　）‎ A．在⊙O内 B．在⊙O上 ‎ C．在⊙O外 D．与⊙O的位置关系无法确定 ‎4、如图，△AOB绕点O逆时针旋转65°得到△COD，若∠AOB＝30°，则∠BOC的度数是（　　）‎ A．30° B．35° C．45° D．60°‎ 第4题图 第5题图 第7题图 ‎5、如图，PA、PB分别切⊙O于点A、B，OP交⊙O于点C，下列结论中，错误的是（　　）‎ A．∠1＝∠2 B．PA＝PB C．AB⊥OP D．OP=2OA ‎6、在Rt△ABC中，∠C＝90°，AB＝6，△ABC的内切圆半径为1，则△ABC的周长（　　）‎ A．13 B．‎14 ‎C．15 D．16‎ ‎7、如图，著名水乡乌镇的一圆拱桥的拱顶到水面的距离CD为‎8m，水面宽AB为‎8m，则桥拱半径OC为（　　）‎ A．‎4m B．‎5m C．‎6m D．‎‎8m ‎8、若钟表分针走30分钟，则钟表的时针转 （ ）‎ ‎ A． B． C． D．‎ ‎9、如图，如果AB为⊙O的直径，弦CD⊥AB，垂足为E，那么下列结论中，错误的是（ ）．‎ A．CE=DE B．弧BC =弧 BD C．∠BAC=∠BAD D．AC>AD 第9题图 第11题图 第12题图 ‎10、一个图形无论经过平移还是旋转，有以下说法正确的是 （ ）‎ ‎①对应线段平行 ②对应线段相等 ③对应角相等 ④图形的形状和大小都没有变化 A、 ‎①②③ B、①②④ C、①③④ D、②③④‎ ‎11、如图，在圆内接四边形ABCD中，若∠A，∠B，∠C的度数之比为4∶3∶5，则∠D的度数是（ ）‎ A． B． C． D．‎ ‎12、如图，把Rt△OAB置于平面直角坐标系中，点A的坐标为（0，4），点B的坐标为（3，0），点P是Rt△OAB内切圆的圆心．将Rt△OAB沿x轴的正方向作无滑动滚动，使它的三边依次与x轴重合，第一次滚动后圆心为P1，第二次滚动后圆心为P2，…，依此规律，第2019次滚动后，Rt△OAB内切圆的圆心P2019的坐标是（ ）‎ A． B． C． D． ‎ 二、填空（每题3分，共18分）‎ ‎13．如图，∠D＝48°，则∠AOC的度数是______．‎ ‎14．两直角边分别为3、4的直角三角形的内切圆半径是 。‎ ‎15．两边长分别为‎6cm、‎8cm的直角三角形的外接圆半径是　 　 cm ‎17图 ‎16.如图，AB为⊙O的直径，CD为⊙O的弦，，的度数为______． ‎ 第13题图 第16题图 ‎17、如图17：AB，BC，CD分别与⊙O相切于E，F，G，BE=4，CG=6，则BC= ‎ ‎18、以下命题中，正确的有 。‎ ‎(1)过三点一定有一个圆 （2）同弧所对的圆周角相等 （3）直径所对的圆周角是直角 ‎（4）平分弦的直径垂直弦，并且平分弦所对的两段弧 （5）相等的弦所对的圆周角相等 ‎（6）三角形的外心是三内角角平分线交点 （7）三角形的内心是三内角角平分线交点 ‎ ‎（8）圆心到直线上一点的距离等于半径，则直线是圆的切线 三、解答题（共66分，其中19---22题8分，23题各10分，24、25各12分）‎ ‎19、（8分）如图，已知三个顶点坐标分别是，，‎ ‎．请按要求画图： 画出关于原点O中心对称后得到的； 画出绕着原点O顺时针旋转后得到的． 请写与的坐标．‎ ‎20．（8分）如图，AB为⊙O的直径，C为⊙O上一点，AD和过C点的直线互相垂直，垂足为D，且AC平分∠DAB．‎ ‎（1）求证：DC为⊙O的切线；‎ ‎（2）若∠DAB＝60°，⊙O的半径为3，求线段CD的长．‎ ‎21、（8分）OA是⊙O的半径，以OA为直径的⊙C与⊙O的弦AE相交于点D，‎ ‎（1）求证：点D是AE的中点，‎ ‎（2） 若DO = 5 ，且求的面积 ‎22．（8分）如图，等边△ABC内接于⊙O，P是弧AB上任一点（点P不与点A、B重合），连接AP、BP，过点C作CM∥BP交PA的延长线于点M．‎ ‎（1）求∠APC的度数．‎ ‎（2）求证：△PCM为等边三角形．‎ 23、 ‎（10分）如图，在Rt△ABC中，∠C=90°，点O在AB上，经过点A的○O与BC相切于点D，与AC、AB分别相交于点E、F，连接AD与EF相交于点G。‎ （1） 求证：AD平分∠CAB；‎ （2） 若OH⊥AD于点H，FH平分∠AFE，‎ 试判断DF与DH的数量关系，并说明理由。‎ 24、 ‎（12分）如图，在中，CA是边BE上的中线，,CE交BA的延长线于点E，BE = 10 ，BC = 8.‎ (1) 求证：为等腰三角形 (2) 求CE的长 ‎ (3) 求的外接圆圆心P与内切圆圆心Q之间的距离 ‎25.（12分）如图，已知直线：和抛物线：，抛物线的顶点为原点，且经过点，直线与轴交于点，与抛物线L交于点、，且.‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P是抛物线上的一个动点，‎ ‎①以点P为圆心，PF为半径作⊙P，试判断⊙P与直线的位置关系，并说明理由；‎ ‎②若点，当的值最小时，求点的坐标；‎ ‎（3）求证：无论为何值，直线总是与以为直径的圆相切.‎ ‎ ‎ 明达中学初三第一次月考 数学答案 一.选择题（本大题共12小题，每小题3分，共36分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B D A B D B B B D D D D 二.填空题（本大题共6小题，每小题3分，18分）‎ ‎13. 14. 15. 5 16. 65° 17. 10 18. ②③⑦‎ 三、解答题（本大题共7小题，共66分）‎ 19、 解：（1）图略 （2） 图略 （3） ‎20.（1）证明：连接CO，‎ ‎∵AO＝CO，‎ ‎∴∠OAC＝∠OCA，‎ ‎∵AC平分∠DAB，‎ ‎∴∠OAC＝∠DAC，‎ ‎∴∠DAC＝∠OCA，‎ ‎∴CO∥AD，‎ ‎∴CO⊥CD，‎ ‎∴DC为⊙O的切线；…………4分 ‎（2）连接BC，‎ ‎∵AB为⊙O的直径，‎ ‎∴∠ACB＝90°，‎ ‎∵∠DAB＝60°，AC平分∠DAB，‎ ‎∴∠BAC＝∠DAB＝30°，‎ ‎∵⊙O的半径为3，‎ ‎∴AB＝6，‎ ‎∴AC＝AB＝3．…………6分 ‎∵∠CAD＝30°‎ ‎∴……………8分（注意：方法不唯一，也可过点O作OE垂直AD于点E,四边形OCDE为矩形，OE=CD,求出OE即可）‎ ‎21、（1）联结OD，‎ ‎ 是⊙C的直径 ‎ ‎ ‎ 又在⊙O中，OD过圆心 ‎ ‎ ‎ 即：D是AE的中点 ‎ (2)‎ ‎ ‎ ‎22.解：（1）∵△ABC是等边三角形，‎ ‎∴∠ABC＝60°，‎ ‎∴∠APC＝∠ABC＝60°；……………………4分 ‎（2）∵∠BPC＝∠BAC＝60°，‎ 又CM∥BP，‎ ‎∴∠PCM＝∠BPC＝60°，‎ 又由（1）得∠APC＝60°，‎ ‎∴△PCM为等边三角形；……………………8分 ‎23、（1）证明：连接OD． ∵⊙O与BC相切于点D， ∴OD⊥BC， ∵∠C=90°， ∴OD∥AC， ∴∠CAD=∠ODA， ∵OA=OD， ∴∠OAD=∠ODA， ∴∠CAD=∠BAD， ∴AD平分∠CAB．‎ ‎（2）DF=DH 理由如下：∵FH平分∠AFE， ∴∠AFH=∠EFH， ∵∠DFG=∠EAD=∠HAF， ∴∠DFG=∠EAD=∠HAF， ∴∠DFG+∠GFH=∠HAF+∠HFA， 即∠DFH=∠DHF， ∴DF=DH，‎ ‎24、(1)‎ ‎ ‎ ‎（3）‎ 即外心P和内心Q的距离是 25． ‎（1）解：∵的顶点为原点，‎ ‎∴，‎ ‎∴抛物线解析式为，……………………1分 把点代入得到，……………………2分 ‎∵，∴，‎ ‎∴抛物线解析式为．………………3分 （2） ‎①⊙P与直线相切. 理由如下：‎ 设为抛物线L上任意一点，作PM⊥直线于M，‎ ‎ 由可得 ‎∴，‎ ‎∴（半径）‎ ‎∴ ⊙P与直线相切 ‎② 由①知，抛物线L上任意一点到点F的距离与到直线l 的距离相等 ‎∴当PQ⊥直线l时，的值最小，此时 ‎ ‎（3）证明：由，得．‎ ‎∴，，‎ ‎∴ ‎ 设BC中点为，过点作于点D，‎ 则点坐标为，‎ ‎∴‎ ‎∴无论为何值，直线总是与以BC为直径的圆相切； ‎