- 2021-10-26 发布 |
- 37.5 KB |
- 4页

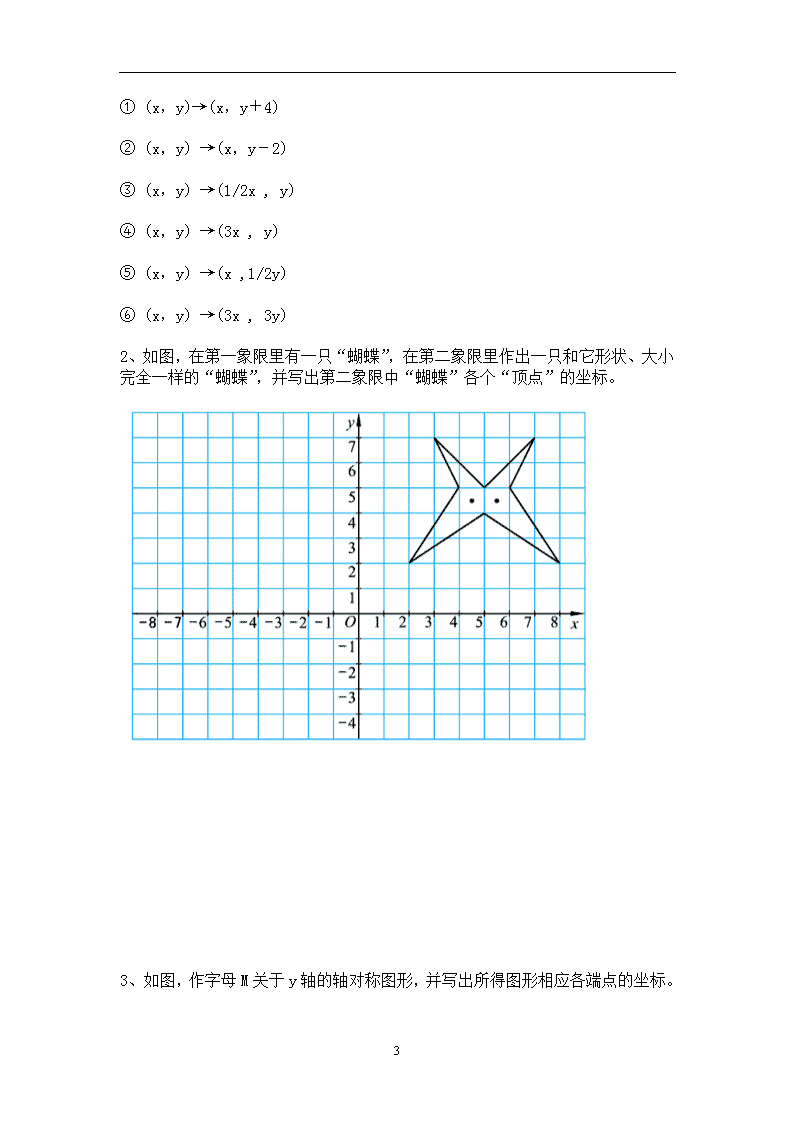
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
变化的鱼学案(二)
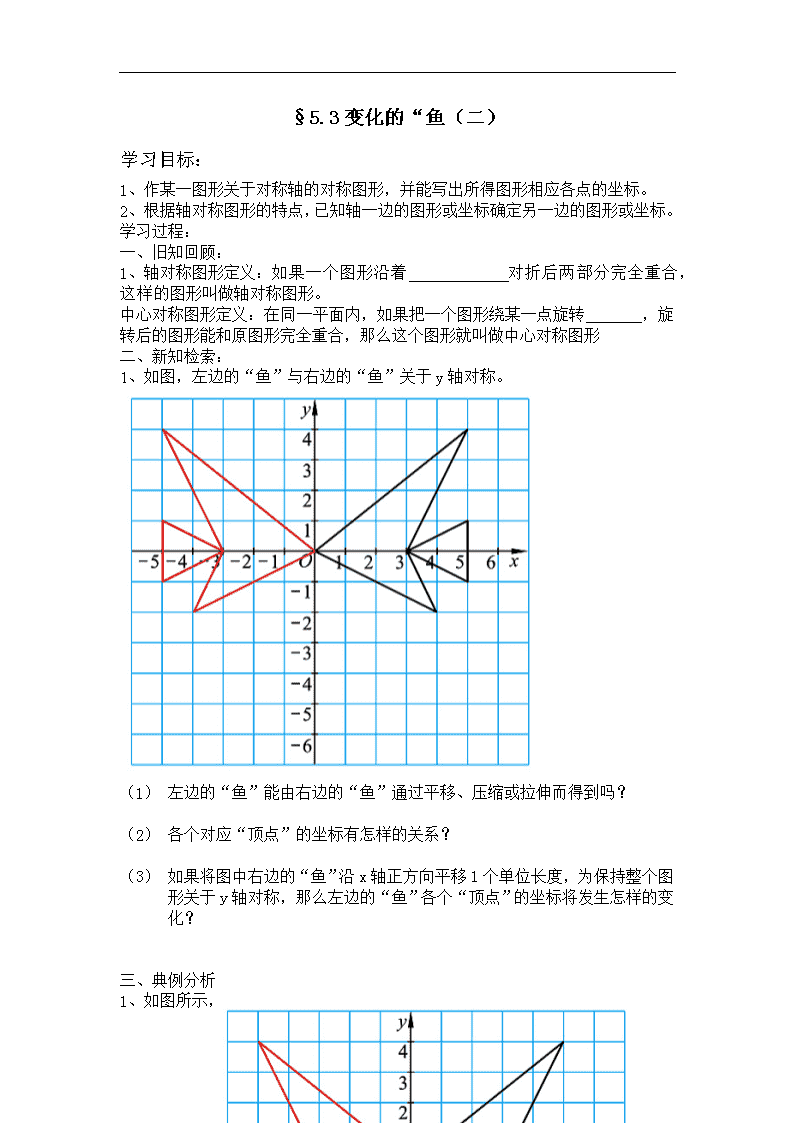
§5.3变化的“鱼(二) 学习目标: 1、 作某一图形关于对称轴的对称图形,并能写出所得图形相应各点的坐标。 2、 根据轴对称图形的特点,已知轴一边的图形或坐标确定另一边的图形或坐标。 学习过程: 一、旧知回顾: -2 1、轴对称图形定义:如果一个图形沿着 对折后两部分完全重合,这样的图形叫做轴对称图形。 中心对称图形定义:在同一平面内,如果把一个图形绕某一点旋转 ,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形 二、新知检索: 1、如图,左边的“鱼”与右边的“鱼”关于y轴对称。 三、典例分析 例1、 (1) 左边的“鱼”能由右边的“鱼”通过平移、压缩或拉伸而得到吗? (2) 各个对应“顶点”的坐标有怎样的关系? (3) 如果将图中右边的“鱼”沿x轴正方向平移1个单位长度,为保持整个图形关于y轴对称,那么左边的“鱼”各个“顶点”的坐标将发生怎样的变化? 三、典例分析 1、如图所示, 4 (1) 右图的“鱼”是通过什么样的变换得到 左图的“鱼”的。 (2) 如果将右边的“鱼”的横坐标保持不变,纵坐标分别变为原来的—1倍,画出图形,得到的“鱼”与原来的“鱼”有什么样的位置关系。 (3) 如果将右边的“鱼”的纵、横坐标都分别变为原来的—1倍,得到的“鱼”与原来的“鱼”有什么样的位置关系 四、题组练习 1、将坐标作如下变化时,图形将怎样变化? 4 ① (x,y)→(x,y+4) ② (x,y) →(x,y-2) ③ (x,y) →(1/2x , y) ④ (x,y) →(3x , y) ⑤ (x,y) →(x ,1/2y) ⑥ (x,y) →(3x , 3y) 2、如图,在第一象限里有一只“蝴蝶”,在第二象限里作出一只和它形状、大小完全一样的“蝴蝶”,并写出第二象限中“蝴蝶”各个“顶点”的坐标。 1、 如图,作字母M关于y轴的轴对称图形,并写出所得图形相应各端点的坐标。 4 1、 描出下图中枫叶图案关于x轴的轴对称图形的简图。 4查看更多