六年级下册数学试题-小升初：第十三讲 策略与操作（解析版）全国通用

六年级下册数学试题-小升初：第十三讲 策略与操作（解析版）全国通用

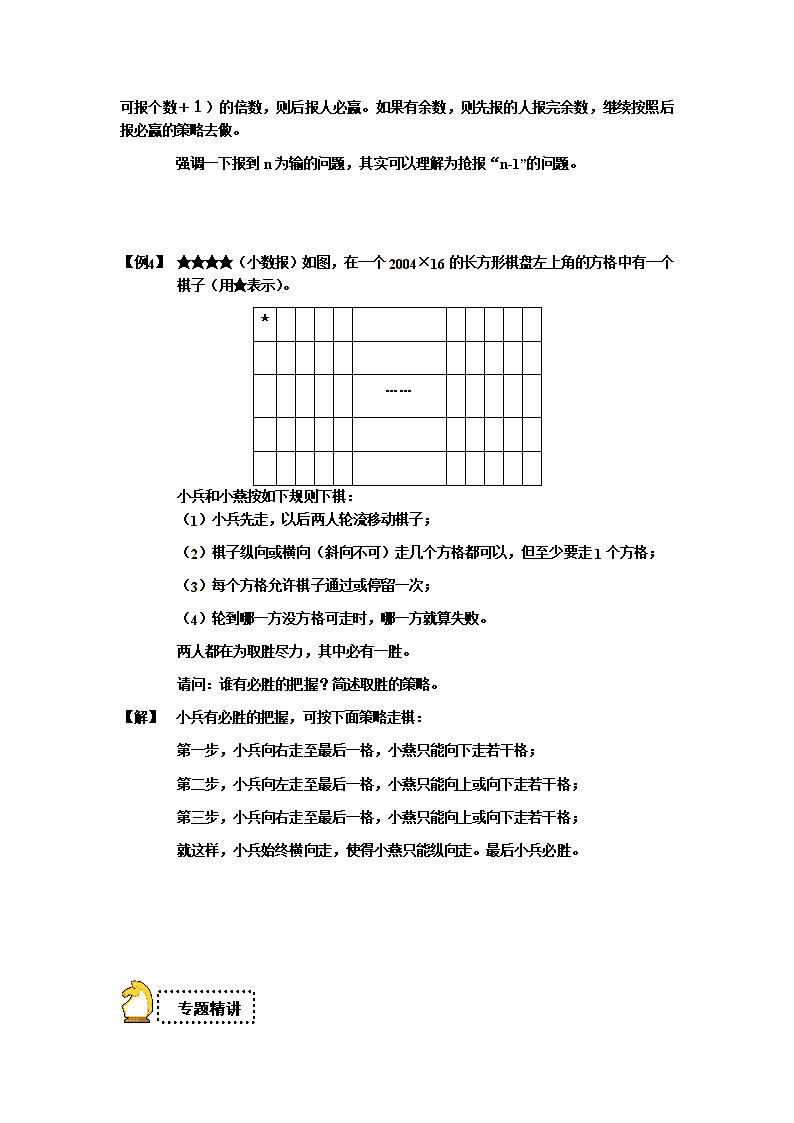
第十三讲 策略与操作 在许多情况下，策略问题与操作联系在一起，要下一种结论，我们往往要找到适当的“证明”方法。有时候，我们通过找规律（归纳法），从正面证明，有时候，我们通过反证法，从反面证明。‎ 教学目标 ‎ 1、回顾：对策问题 ‎2、精讲：操作问题。‎ 专题回顾 断链问题 【例1】 ‎★★（《小数报》数学竞赛初赛应用题第2题）‎ 锻工师傅收到五段铁链，每段有三个环（如图）要求连成一条铁链，你认为至少打开几个环，才能连成一条铁链？‎ ‎【解】 至少打开3个环，因为打开2个环，只能连结三段铁链，而将一段铁链的3个环全打开，就可以将其余四段全连结起来。‎ 【例2】 ‎★★★有个吝啬的老财主，总是不想付钱给长工。这一次，拖了一个月的工钱，还是不想付。可是不付又说不过去，便故作大方地拿出一条金链，共有7环。对长工说：“我不是要拖欠工资，只是想连这一个月加上再做半年的工资，都以这根金链来付。”他望向吃惊的长工，心中很是得意，“本人说话，从不食言，可以请大老爷作证。”大老爷可是说一不二的人，谁请他作证，他当作一种荣耀，总是分文不取，并会以命相拼也要兑现的。这越发让长工不敢相信，要知道，这在以往，这样的金链中的一环三个月的工钱也不止。老财主越发得意，终于拿出杀手锏：“不过，我请大老爷作证的时候，提到一项附加条件，就是这样的金链实在不能都把它断开，请你只能打开一环，以后按月来取才行！”当长工明白了老财主的要求后，不仅不为难，反倒爽快地答应了，而且，从第一个月到第七个月，顺利地拿到了这条金链，你知道怎么断开这条金链吗？‎ ‎【解】 断开第三环，从而得到1，2，4环的三段，第一个月拿走一环，第二个月以一换二，第三个月再取一环，第四个月以三换四，第五个月再取一环，第六个月以一换二，第七个月再取一环。‎ 必胜之道 【例1】 ‎★★小明与弟弟在玩一种“抢报30”的游戏。从1开始到30,两人轮流报数，每人每次最多报两个数，谁先抢到“30”算赢。请问，在他们先报与后报的人中，谁有必胜的策略。‎ ‎【解1】 可以用倒推法，抢到“30”的人，必需“抢到”27、24、21、……3，所以，先报的人必输，后报的人必赢。即后报的人，结合先报的人的报数情况，使每个回合共报3个数即可。‎ ‎【解2】 一般来说，在抢报“30”的游戏中，开始可以确定一下策略，就是如何使“30”处于一个回合中的最后一个，（后取者必胜），因为30个数正好是一个回合（1+2=）3的倍数。‎ ‎【拓展】对于抢报50，最多可取三个数的情况，谁取到“50”为输。请问必胜的策略是什么呢？‎ ‎【解】 对于后取到，则要考虑“逼将”的方法，必须在N个回合之后，只余下“50”来，从倒推角度看就是要“抢到”49、因为这次的游戏规则是每个回合为（1+3=）4，所以，49÷4=12…1，则先报的人第一次只报1，接着“配合”对方，每个回合共报4个数，必使对方报“50”。‎ ‎【点评】一般地，如果是“抢报”n,把n放在每个回合的最后一个，如果n是回合（最多可报个数＋１）的倍数，则后报人必赢。如果有余数，则先报的人报完余数，继续按照后报必赢的策略去做。‎ ‎ 强调一下报到n为输的问题，其实可以理解为抢报“n-1”的问题。‎ 【例1】 ‎★★★★（小数报）如图，在一个2004×16的长方形棋盘左上角的方格中有一个棋子（用★表示）。‎ ‎★‎ ‎……‎ 小兵和小燕按如下规则下棋： （1）小兵先走，以后两人轮流移动棋子；‎ ‎（2）棋子纵向或横向（斜向不可）走几个方格都可以，但至少要走1个方格；‎ ‎（3）每个方格允许棋子通过或停留一次；‎ ‎（4）轮到哪一方没方格可走时，哪一方就算失败。‎ 两人都在为取胜尽力，其中必有一胜。‎ 请问：谁有必胜的把握？简述取胜的策略。‎ ‎【解】 小兵有必胜的把握，可按下面策略走棋：‎ 第一步，小兵向右走至最后一格，小燕只能向下走若干格；‎ 第二步，小兵向左走至最后一格，小燕只能向上或向下走若干格；‎ 第三步，小兵向右走至最后一格，小燕只能向上或向下走若干格；‎ 就这样，小兵始终横向走，使得小燕只能纵向走。最后小兵必胜。‎ ‎ ‎ 专题精讲 染色法 【例1】 ‎★★★（小学数学夏令营活动试题）‎ 有一个5×5的方格棋盘，每一个小方格中有一只小甲虫，假定在同一时刻，所有小甲虫都爬到邻格中（横向与纵向的格，不能斜爬），问此时能否会出现空格？‎ ‎【解】 初看这个问题，似乎无从下手，但如果我们利用“染色”的手段，就会使问题简化，很轻松的得到正确答案.将5×5棋盘用黑白两种颜色相间染色，如图所示，此时共有黑格13个，白色格12个.当每个小格中的甲虫同时爬向邻格时，即黑格中的甲虫爬到白格中，白格中的甲虫爬到黑格中，由于黑格比白格多一格，则原来白格中的甲虫爬到黑格后必空一格，所以该题的答案是肯定的。 ‎ 归纳法 【例2】 ‎★★★★（“华罗庚金杯”数学邀请赛）先写出一个两位数62，接着在62右端写这两个数字的和8，得到628，再写末两位数字2和8的和10，得到62810，用上述方法得到一个有2006位的整数：‎ ‎6 2 8 1 0 1 1 2 3 ……‎ 则这个整数的数字之和是（ ）。‎ ‎【解】7018。‎ 这个2006位整数的前若干位如下：‎ ‎62810┊1123581347┊11……‎ 从第6位起，每10位数字循环出现一次，这10位数字之和为 ‎1 + 1 + 2 + 3 + 5 + 8 + 1 + 3 + 4 + 7 = 35。‎ ‎（2006－5）÷10=200……1，‎ 这个整数的数字之和是 ‎6 + 2 + 8 + 1 + 0 + 35×200 + 1 = 7018。‎ 【例3】 ‎★★★（西城八中入学选拔试题）‎ A、B、C、D四个盒子中依次放有6，4，5，3个球。第1个小朋友找到放球最少的盒子，从其他盒子中各取一个球放入这个盒子；然后第2个小朋友找到放球最少的盒子，从其他盒子中合取一个球放入这个盒子；如此进行下去，……。求当34位小朋友放完后，B盒子中放有球多少个？‎ ‎【解】盒 子 A B C D ‎ 初始状态 6 4 5 3‎ ‎ 第1人放过后 5 3 4 6‎ ‎ 第2人放过后 4 6 3 5‎ ‎ 第3人放过后 3 5 6 4‎ ‎ 第4人放过后 6 4 5 3‎ ‎ 第5人放过后 5 3 4 6‎ ‎ 由此可知：每经过4人，四个盒子中球的情况重复出现一次，因为34÷4=8…2，所以第34次后的情况与第2次后的情况相同，即B盒子中有球6个 操作法 【例1】 ‎★★★将7×7的方格纸(如下页图)剪成1×5和2×3的长方形，使得剩余的残料尽可能少。残料最少是几个小方格？‎ ‎【解】0。提示：7×7的方格纸共有49个小方格。5×5+4×6=49，即5个l×5加上4个2×3的长方形正好是49个小方格。经过试验可拼成下图。‎ 【例2】 ‎★★★★‎ ‎（《小学生数学报》读报竞赛）把一张正方形的餐巾纸先上下对折，再左右对折（如右图），然后用剪刀将所得的小正方形沿直线剪一刀。问能把餐巾纸：‎ ‎（1）剪成2块吗？‎ ‎（2）剪成3块吗？‎ ‎（3）剪成4块吗？‎ ‎（4）剪成5块吗？‎ ‎ 如果你认为能剪成，请在下面图中各画出一种你的剪法；如果你认为不能，那么只需回答“不行”即可。‎ ‎（1）剪开成两块，如下图：‎ ‎（2）剪开成3块，如下图：‎ ‎（3）剪开成4块，如下图：‎ ‎（4）剪开成5块，如下图：‎ 枚举法 【例1】 ‎★★★有6张电影票(如下图)，想撕成相连的3张，共有多少种不同的撕法？‎ ‎【解】：形如的有2种，形如的有8种。‎ 【例2】 ‎★★★大、小两枚骰子，每枚骰子的六个面分别画着1～6个点。同时抛这两枚骰子，两枚骰子的点数之差等于1与等于2的可能性相比，等于几的可能性大。‎ ‎【解】：点数之差等于1时，大骰子的点数由1到6对应小骰子的点数如下，共10种情况：‎ ‎ 1 2 3 4‎ ‎1 2，2 , 3 , 4 , 5 ,6 5‎ ‎ 3 4 5 6‎ 点数之差等于2时，共8种情况：‎ ‎ 1 2‎ ‎1 3,2 4，3 5 ,4 6，5 3,6 4‎ 所以等于1的可能性大。 ‎ 建模法 【例3】 ‎★★★有一叠300张卡片，从上到下依次编号为1~300，从最上面的一张开始按如下的顺序进行操作：把最上面的第一张卡片拿掉，把下一张卡片放在这一叠卡片的最下面；再把最上面的依次重复这样做，直到手中剩下一张卡片。那么剩下的这张卡片是原来300张卡片的第几张？‎ ‎【解】 88张。‎ 当有256=28‎ ‎（张）卡片时，第一轮过后剩下的是2的倍数号卡片，第二轮过后剩下的是22的倍数号卡片……第8轮过后，剩下的是28的倍数号卡片，即就剩下1张卡片，是第256号卡片。‎ 现在有300张卡片，如果拿掉300－256=44（张）卡片，剩下256张卡片，那么就变为上述的情况了。拿掉的第44张卡片是编号为44×2－1=87（号）的卡片，此时剩下256张卡片，下一个要拿掉的是第89号卡片，第88号是最后一张。所以，剩下的这张卡片是原来的第88张。2‎ ‎【点评】关键是从模型2n中找到规律，这种规律的前提是2n个数，这就要考量怎么转换条件的问题。‎ ‎【拓展】猫捉耗子问题（奥数网学员研究心得）‎ 专题展望 欲看奥数精彩，敬请继续关注：暑假班下一讲“IQ与数学应用”‎ ‎ ‎ 真题实战 ‎1、（仁华试题）‎ 现有2.8米长的方木条原料，要截成1.2米、0.9米两种长度的木条作镜框（每个镜框要用长、短木条各两根）.要做30个镜框，如何下料可以最省？‎ ‎【解】：这是个节约用料的问题.如果不精打细算就会简单的用一根原料截长短木条各一根，就样就需要60根原料.而这样就会造成很大的浪费.因为每根原料剩下的残料为2.8-1.2-0.9=0.7（米）， 60根原料所剩的残料则是很大的一个数字，显然这不是最佳的方案。如果我们考虑用一根原料分别截取长短木条，则：（1）可截1.2米木条两根，余料0.4米；（2）可截0.9米木条三根，余料0.1米。现设取x根原料用于截法（1）：取y根原料用于截法（2）.则有 故需要原料50根即可制成30个镜框。‎ ‎2、两人作移火柴棍的游戏，游戏的规则如下：两人从一堆火柴棍中可轮流移走1－7根，直到移尽为止。挨到谁移最后一根就算谁输。如果开始时有1000根火柴，则先移的人第一次应该移动（　　）根火柴棍，才能保证在游戏中获胜。‎ ‎【解】7。先取者必须首先移走7根火柴，才能保证在游戏中获胜，其获胜的方法是以后每次移走的火柴数与后移者刚刚移走的火柴数加起来等于8。这样由于1000－7＝993，而993/8＝124余1，最后一根火柴总是被后移者移走。‎ ‎3、将前100个自然数顺次写下得到多位数12345678910…….100，从首位起将这些数位从1开始编号，然后划去编号是奇数的数位上的数字，这样便形成一个位数较少的多位数，重复上述这种划去数字操作，直至得到一个三位数，则这个三位是（　　）。‎ ‎【解】第一次操作后，剩下的全都是偶数位的数字 第二次操作后，剩下的全是4的倍数位上的数字；‎ ‎……………‎ 直到第六次操作后，剩下的全是64的倍数位上的数字，‎ 原多位数一共有9＋2＊90＋3＝192位，所以此时剩下的是第64位、128位和192位上的数字。‎ ‎64－9＝55,55/2＝27……..1，所以第64位上的是“37”的“3”；128－9＝119,119/2＝59…..1，所以第128位上的是“69”的“6”，所以剩下的三位数是360。）‎ ‎4、A、B、C、D、E、F、G共7位先生参加一次聚会，期间他们中有些人相互握手，并且两个人之间至多握一次手，最后A、B、C、D、E、F回忆各自握手次数依次为6、6、5、4、4、2，并且D和E没有握手，那么G握了（　　　　　　）次手。‎ ‎【解】5。首先可注意到A、B和每个人握了手，由F只握了两次手可知他与C、D、E、G都没握手，从而由以C握了5次手得到他只没有和F握手，即和G握过手，由于D、E没有握手且他们都没有和F握手，而他们分别握了4次手，所以他们都和G握过手，从而G仅没有和F握手，即他握了5次手。‎ ‎5、黑板上写着1,2，3,4……200各一个，小明每次擦去两个奇偶性相同的数，再写上它们的平均数，最后黑板上只剩下一个自然数，这个数最大是（　　）。‎ ‎【解】由于平均数不会大于原来较大的数，所以该数不可能大于200，又因为一开始只有一个200，所以平均数肯定比200小。如果擦去1和3，写上2再擦去2和2，仍写上2，擦去2和4，写上3，再擦去3和3，仍写上3；……….‎ 擦去198和200写上199，再擦去199与199，仍写上199，这样最后只剩下199，所求答案为199。）‎ 数学语絮 祖冲之和圆周率的故事 ‎ 祖冲之出身于南朝刘宋的一个官员家庭。从青年时代他就致力于天文和数学等领域的研究。晋朝时的刘徽用“割圆术”从边长为l尺的正六边形开始分割，以周长除以直径，求得圆周率为3.141024。祖冲之继续刘徽的工作算到圆内接正24576边形，求得是介于下面两数之间：3.1415926< <3.1415927。祖冲之并以分数来代表圆周率的近似值，称为“密率”。西方世界在祖冲之以后1000年才找出这个近似，值。因此有人建议将这个圆周率的近似值，称为“祖率”，以纪念祖冲之的贡献。祖冲之不论是对的计算或“密率”的提出，都比外国科学家早了1000多年，这正是祖冲之对数学的卓越贡献。祖冲之享有很高的国际声誉，月球上有一座山用他的名字命名(“祖冲之山”)就是一个例证。‎ ‎ 那么，祖冲之是怎样求出的呢?祖冲之先是在地上画一个直径为1丈的大圆，又按照刘徽所用的割圆术，在圆内做一个内接正六边形。每边与半径一样长，半径长是5尺，所以每边长也是5尺。后来，祖冲之再把六边形所对的六个圆弧平分，做出了正十二边形，用尺子一量，每边长是2尺6寸多。他想用尺子量只是一个大概，要想求出精确的解必须用数字才行，因此他又叫来自己的儿子祖恒过来用竹制的算筹帮忙。到后来，每个数字都会拖得长长的。每算完一步，祖恒都要在旁边记录一下结果。‎ ‎ 父子俩个算到半夜，直到灯油快干了，才算出来十二边形的每边长0.258819丈，总长是3.105828丈。“儿子，咱们终于算出来了!”祖冲之拍了拍儿子的肩头说。辛苦了大半夜终于有了一点收获，祖冲之再次端详了一下这个来之不易的数字，便陪着儿子一块睡觉去了。第二天，父子两个又投入到紧张的计算工作中去。这天晚上，父子俩又按照昨晚的计算思路计算了圆内接正二十四边形的长度。‎ ‎ 在儿子的协助下，祖冲之又相继计算出了圆内接正四十八边形、九十六边形……边数越多，每边的长度也就越小，正12288边形每边的长为0.00025566丈。祖冲之认为，从理论上来说，把圆周这样分割下去是无穷无尽的，但是事实上目前已经不能再分割下去了。因此，当时祖冲之就只能分割到24576边形就得到了结论：圆的周长与直径的比值在3.1415926和3.1415927之间，这样就比较精确地计算出了圆周率的值。‎ 附加习题 【附1】 ‎（学而思学生数学小论文）‎ 猫捉耗子是一个有名的游戏，一只猫让N个老鼠围成一圈报数，每次吃掉报单数的老鼠，有一只老鼠总不被吃掉，问这个老鼠站在哪个位置？数学中称这类问题为猫捉耗子问题。对这类问题通常的做法是从特殊情况出发，逐步发现规律，然后给出求解公式。老师在课堂上介绍了公式以及推导过程，但我认为推导过程较为复杂，不好理解。根据反复试验和观察，本文给出了一种容易理解的求解这类问题的方法。 ‎ 方法和例子 ‎ ‎    这里列举这类问题的两种情形。对于每种情形都首先考虑特殊情况，然后从中发现规律。这两种情形都是基于如下前提：从1到N编号的N个老鼠顺时针围成一圈，从1开始报数。并规定游戏一开始的第一个生存者是1号老鼠。设老鼠的总个数为N，最后幸存的老鼠编号为X。 ‎ 情形1：‎ ‎    1号老鼠生存下来，2号老鼠被猫吃掉；3号老鼠生存下来，4号老鼠被猫吃掉.....就这样，这只猫每隔一只老鼠，就吃掉另一只老鼠，那么最后唯一幸存的那只老鼠是几号呢？ ‎ ‎    先考虑简单的情况。当有两只老鼠围成一圈时，猫吃掉了2号，1号为最后的幸存者；当有三只老鼠围成一圈时，猫先吃掉了2号，然后是1号，最后的幸存者是3号.....，依次类推，可发现如下规律： ‎ N ‎ ‎2 ‎ ‎3 ‎ ‎4 ‎ ‎5 ‎ ‎6 ‎ ‎7 ‎ ‎8 ‎ ‎9 ‎ ‎10 ‎ ‎11 ‎ ‎12 ‎ ‎13 ‎ ‎14 ‎ ‎15 ‎ ‎16 ‎ ‎17 ‎ ‎18 ‎ ‎19 ‎ ‎20 ‎ ‎... ‎ X ‎ ‎1 ‎ ‎3 ‎ ‎1 ‎ ‎3 ‎ ‎5 ‎ ‎7 ‎ ‎1 ‎ ‎3 ‎ ‎5 ‎ ‎7 ‎ ‎9 ‎ ‎11 ‎ ‎13 ‎ ‎15 ‎ ‎1 ‎ ‎3 ‎ ‎5 ‎ ‎7 ‎ ‎9 ‎ ‎... ‎ ‎ ‎ ‎ ‎ ‎  对于这种情况，每次猫都是从两只老鼠中吃掉一只老鼠，可认为2只为一个周期，用m＝2表示；用n表示每个周期内吃掉的老鼠数目，这里是n=1。‎ 情形2：‎ ‎    1号老鼠生存下来，2号、3号老鼠被猫吃掉；4号老鼠生存下来，5号、6号老鼠被猫吃掉.....就这样，这只猫每隔一只老鼠，就吃掉另两只老鼠，依次下去，最后唯一幸存的那只老鼠是几号呢？ ‎ ‎    先考虑简单的情况。当有三只老鼠围成一圈时，猫吃掉了2号和3号，1号为最后的幸存者；当五只老鼠围成一圈时，猫先吃掉了2号和3号，然后是5号和1号，最后的幸存者是4号.....，依次类推，可发现如下规律： ‎ N ‎ ‎3 ‎ ‎5 ‎ ‎7 ‎ ‎9 ‎ ‎11 ‎ ‎13 ‎ ‎15 ‎ ‎17 ‎ ‎19 ‎ ‎21 ‎ ‎23 ‎ ‎25 ‎ ‎27 ‎ ‎29 ‎ ‎31 ‎ ‎33 ‎ ‎... ‎ ‎81 ‎ ‎83 ‎ ‎... ‎ X ‎ ‎1 ‎ ‎4 ‎ ‎7 ‎ ‎1 ‎ ‎4 ‎ ‎7 ‎ ‎10 ‎ ‎13 ‎ ‎16 ‎ ‎19 ‎ ‎22 ‎ ‎25 ‎ ‎1 ‎ ‎4 ‎ ‎7 ‎ ‎10 ‎ ‎... ‎ ‎1 ‎ ‎4 ‎ ‎... ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎    对于这种情况，每次猫都是从三只老鼠中吃掉两只，可认为3只为一个周期，即m＝3；每3只中吃掉两只，因此，n=2。‎ 结论 ‎ ‎    通过对上述两种情形的运算结果的观察，发现N的所有可能的取值按照一定的顺序排列后，构成了一个等差数列A。该数列的首项a1＝m，公差d＝n（m和n都是正整数）。 ‎ ‎    而与N对应的X的取值则构成了若干个等差数列B1，B2，...，Bk。这些等差数列的公差都为m，首项都为1。还发现，构成的这些等差数列有这样一个规律：每逢N的值为mk时（m和k都是正整数），对应X的取值就是1。也就是说，当N的取值范围从mk到mk+1－n 之间时，对应的X的取值就构成了一个d=m，a1=1的等差数列，项数就是从N=mk到N=mk+1－n之间数的个数（包括mk和mk+1－n这两个数）。 ‎ ‎    那么现在来看看一般情形：如果猫要从m个老鼠中吃掉n个老鼠，那么最后幸存的老鼠是几号呢？由上面的结论，可以得出这样的求解步骤： ‎ ‎    1、 首先找到小于N的一个最大的数mk（k是正整数，并假设N≠mk）；  ‎ ‎    2、 这样就构成一个首项a1＝mk，末项an＝N，公差d＝n的等差数列A，利用公式求出项数b; （即，b = 1 ＋ (N- mk)/n ） ‎ ‎    3、 因为X的每个取值也构成了一个与A对应的等差数列Bk，其中，公差为 m，首项为1，项数为b。利用等差数列求末项公式，求出末项an； ‎ ‎（即，an = 1 + (b-1)*m） ‎ ‎    4、 an就是与N对应的X的值，也就是最后唯一幸存老鼠的编号。 ‎ 本文提出的求解方法，通过带入老师所给出的公式验证后，证明此方法是正确的。‎ 【附1】 聪明的猪 从前，有个叫二愣的屠夫，有杀猪宰羊的好手艺，又雇佣着十几个杀猪能手，在这方圆几十里，算是有名的大屠户了。 　　一天，二愣又要杀猪了。按照惯例，总是由二愣先杀第一头猪。哪知，“老虎也有大意的时候”，只见那头猪刚被翻倒在地，就狠狠地咬了二愣一口，急急地跑进猪圈了。 　　这还了得！二愣气呼呼地追进猪圈里，可是圈里有1000头猪，怎么认得出那头猪呢！ 　　“杀！”随着二愣一声吼，1000头猪全部被强行赶进屠宰场。 　　“都杀了吗？”伙计们怯生生地问。 　　“不。”二愣忽然想出个怪主意，“把这1000头猪排成一行，先杀第一头，然后隔一头杀一头；杀完第一遍后，还是原来的队形，再用同样的方法杀第二遍；这样一遍一遍地杀下去——”二愣停了停说，“最后只留下一头猪。” 　　二愣心想，1000头猪最后只留下一头，看你还能活！ 　　哪里知道，这是一头聪明的猪，趁着混乱，它很快找到了避难的位置，居然躲过了这一刀。 　　 请问，这头猪到底排在什么位置上呢？‎ ‎【解】 29=512 ，这是有活路的吉祥数啊！‎ ‎【拓展】如果形成一圈站立，则要考虑余下512头猪的情况时的最后一头。‎ ‎ 29=512，‎ ‎ （1000-512）×2-1=975（号）‎ ‎ 975+1=976（号）最有活路。‎ 【附1】 四种重量分别是1克，3克，8克和12克的砝码，每种重量都有3个砝码，在称物品重量的时候，砝码只能放在天平的一边，而且每次最多用3个砝码。那么，用这些砝码称物品的重量时，不能称出来的整数克重的物品的最轻重量是多少克？‎ ‎【解】 不能称出来的整数克重的物品的最轻重量是22克，‎ ‎1-21克均可称出，22克则不行 【附2】 编号为1到10的十个果盘里，每盘都盛有水果，共盛放100个，其中第一盘里有16个，并且编号相邻的三个果盘中水果数的和都相等，那么第八个盘中水果最多可能有多少个？‎ ‎【解】因为相邻三个果盘中水果数的和都相等，则第4,7，10盘中的水果与第一盘相同，都有16个，同样第2,3盘所放水果数的和与第56盘所放水果的数的和以及第8、9盘所放水果数的和是相同的，用水果总数减去第1,4，7,10盘中的水果数，再平均分成　3份就得到第8、9盘水果数的和：（100－16＊4）/3＝12个。　要使第8个盘中水果数多，第9盘就要尽可能少，即只有1个，所以第8盘中水果最多可能有11个。‎ 【附3】 沿一条公路旁有10个工厂A1，A2，……A10，准备兴建一个车站要使这10个以车站路程总和最小，车站应建于何处？‎ ‎【解】先从简单的情形考察起。若仅有2个工厂A1，A2。显然车站P在A1、A2间任何点都可以（包括点A1，A2），总路程都等于A1A2两点间路程。‎ 若有3个工厂A1A2A3。车站P建在A1A3间任何地方，对于工厂A1A3路程和没有影响，因此只要车站要A2路程最短即可，故车应建在A2处。‎ 若有4个工厂…..‎ 依此类推，对公路旁的10个工厂A1，A2，……A10，车站可建在A5A6间任意一个地方（包括A5A6）。‎ 事实上，我们还可得到更一般结论：沿一旁有工厂A1，A2，…AN时，‎ 若N＝2K（为偶数）时，车站应建在AK、AK＋1上的任何一点，包括这两点。‎ 若N＝2K＋1（为奇数）时，车站应建在AK＋1处。‎ 【附4】 ‎★★★★（“华罗庚金杯”数学邀请赛）有5个黑色和白色棋子围成一圈，规定：将同色且相邻的两个棋子之间放入一个白色棋子，在异色且相邻的两个棋子之间放入一个黑色棋子，然后将原来的5个棋子拿掉。如果第一幅图的初始状态开始依照上述规定操作下去，对于圆圈上呈现5个棋子的情况，圆圈上黑子最多能有 个。‎ ‎【解】 4。‎ ‎5个棋子2种颜色，至少有2个相同颜色的棋子相邻，所以无论操作多少次，5个棋子中至少有1个是白子，所以黑子最多有4个。实际操作得到：‎