八年级上数学课件- 14-1-4 整式的乘法 课件（共13张PPT）_人教新课标

八年级上数学课件- 14-1-4 整式的乘法 课件（共13张PPT）_人教新课标

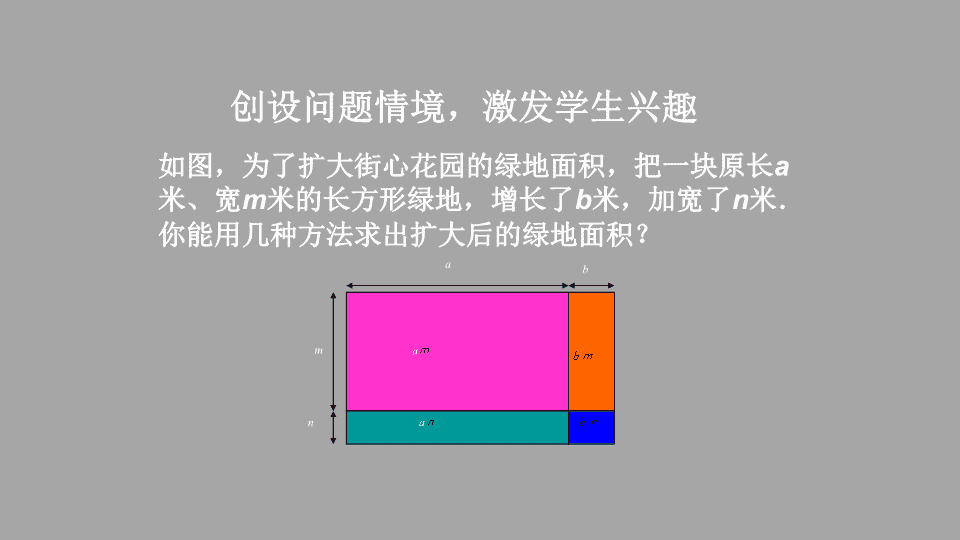
15.1.4整式的乘法 复习回顾计算:(1)(－2a2)·(3ab2－5ab3)(2)(3a2－5b)·2a2(3)－2a2(ab＋b2)－5a(a2b－ab2) 如图，为了扩大街心花园的绿地面积，把一块原长a米、宽m米的长方形绿地，增长了b米，加宽了n米．你能用几种方法求出扩大后的绿地面积？创设问题情境，激发学生兴趣mnabｂｎｂｍaｍaｎ 分析⒈扩大后的绿地面积可以看成一个长方形，其长为(a+b)米，宽为(m+n)米，所以这块绿地的面积为mnabｂｎｂｍaｍaｎ(a+b)(m＋n)米2． ⒉扩大后的绿地面积可以看成由四个小长方形组成，所以这块绿地的面积为因此，(a+b)(m+n)=am+an+bm+bn．上面的等式提供了多项式与多项式相乘的方法.分析mnabｂｎｂｍaｍaｎ（am+an+bm+bn）米2． 推导计算(a+b)(m+n)，可以先把m+n看成一个整体，运用单项式与多项式相乘的法则，得=a(m+n)+b(m+n)=am+an+bm+bn.(a+b)(m+n) 换一种看法，(a+b)(m+n)的结果可以看作由a+b的每一项乘m+n的每一项，再把所得的积相加而得到的，即推导(a+b)(m+n)=am+an+bm+bn 归纳多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.(a+b)(m+n)=am+an+bm+bn． 举例及应用例计算：(1)(3x＋1)(x＋2)；(2)(x－8y)(x－y)(2)(x＋y)(x2－xy＋y2) 1、计算（1）（1－x）（0.6－x）；（2）（x－y）2；（3）（x2+3）（2x－5）；（4）（x+2）（y+3）－（x+1）（y－2）．练习巩固 2、计算：（1）（x+2）（x+3）（2）（x+1）（x－4）（3）（y+4）（y－2）（4）（y－5）（y－3）由上面计算的结果找规律，填空：（x+p）（x+q）=（）2+（）x+（　）p+qpqx 多项式与多项式相乘，先用一个多项式的每一项乘另一个多项式的每一项，再把所得的积相加.小结(a+b)(m+n)=am+an+bm+bn．注意：1、运用法则时，要有序地逐项相乘，做到不重不漏。2、在含有多项式乘法的混合运算时，要注意运算顺序，计算结果要化简。 作业课本习题15.1，第5、6题.