八年级下数学课件：18-1-2 平行四边形的判定 （共19张PPT）1_人教新课标

八年级下数学课件：18-1-2 平行四边形的判定 （共19张PPT）1_人教新课标

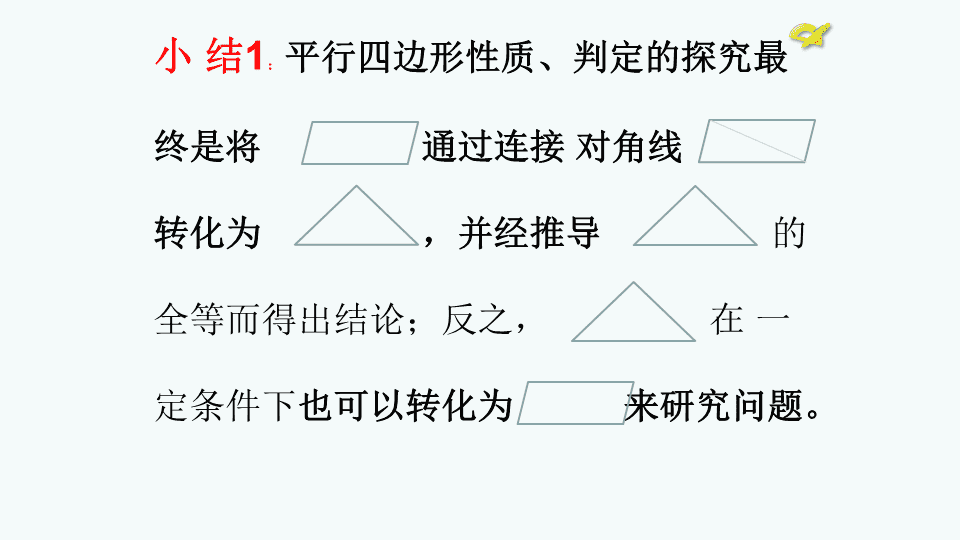
zx``xk§18.1.2平行四边形的判定-----三角形的中位线及定理第十八章平行四边形§18.1平行四边形 复习1、平行四边形的定义？边2、平行四边形的性质定理？角对角线3、平行线间的距离？边4、平行四边形的判定定理？角对角线 小结1：平行四边形性质、判定的探究最终是将通过连接对角线转化为，并经推导的全等而得出结论；反之，在一定条件下也可以转化为来研究问题。 如图，直线L1∥L2,在L1，L2上分别截取AD，BC，使AD=BC，连接AB，CD。AB和CD有什么关系？为什么？L1L2ABCD [问题1]1、什么是三角形的中线？一个三角形有几条中线？动手画一画2、如果任意连接三角形的两个中点，……DFEABCABCFDEO DE三角形中位线的定义：像DE这样，连接三角形两边中点的线段叫做三角形的中位线．几何语言：AD=BDAE=CEDE为ABC的中位线 [问题2]一个三角形有几条中位线？三条[问题3]三角形中位线与三角形中线有什么区别？DE端点不同DEFD 探究：1、给你一个三角形，你会剪成四个全等的三角形吗？剪一剪，拼一下看看！为什么？2、在1、的基础上，你会把一个三角形剪一个角，拼成吗？怎么剪？动手试试！ADEBCEDADE提示：通过探究1、2你发现中位线与第三边有什么特殊性了吗？ 3、如图，DE是△ABC的中位线DE与BC有怎样的关系？两条线段的关系位置关系数量关系一、观察、分析：DE与BC的关系二、猜想：DE∥BC？DE度量一下你手中的三角形，看看是否有同样的结论？并用文字表述这一结论．三、度量： 猜想：三角形的中位线平行于三角形的第三边且等于第三边的一半．DE如何证明你的猜想？四、证明： 已知：如图，D、E分别是△ABC的边AB、AC的中点.求证：DE∥BC，．DEF证法1：将△转化为（老师展示过程） 三角形的中位线平行于三角形的第三边且等于第三边的一半．DE∵DE是△ABC中位线，三角形中位线定理：几何语言：∴DE∥BC，DE=BC． DE证明：如图所示延长DE到F，使EF=DE．F∴四边形BCFD是平行四边形．∴△ADE≌△CFE．∴∠ADE=∠F连接FC．∵∠AED=∠CEF，AE=CE，(下面证明同证法1)证法2：借助△≌△，ADCF．∴BDCF．又∵D、E分别为AB、AC的中点证法3：数学变换（旋转、平移），证明过程为今天作业 如图，A、B两点被池塘隔开，在AB外选一点C，连接AC和BC，怎样量出A、B两点间的距离？根据是什么？NM书上p49练习3提示：你想到了几种方法？哪种最简单？ 1.如图，△ABC中，D、E分别是AB、AC中点．（1）若DE=5，则BC=．（2）若∠B=65°，则∠ADE=°．（3）若DE+BC=12，则BC=．1065x2xx+2x=12x=48练习2： 2.若三角形的周长为56cm，则它的三条中位线组成的三角形的周长是()cm．3.已知：如图，△ABC中，BD平分∠ABC，且D为AC的中点，DE∥BC交AB于点E，若EB=4，则线段BC的长为_____．288 如图，在四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA中点．求证：四边形EFGH是平行四边形．四边形问题连接对角线三角形问题（三角形中位线定理）思考：归纳：连接任意的四边形的各边中点的图形为平行四边形 知识方面：三角形中位线概念；三角形中位线定理。思想方法方面：转化思想小结2：1、动手实验（观察、分析、度量）；2、数学变换（旋转、平移等）；3、添加辅助线（借助△≌△）。探究与命题的关系：一、观察、分析；二、猜想；三、度量；四、证明 1、教材P49复习巩固5．3、再顺次连接思考题中所得到的四边形EFGH各边中点，又得到一个新的四边形，并判断这个新四边形是否是平行四边形？说明理由。课后作业：2、大练习册P323、4、7题