八年级下数学课件：17-1 勾股定理 （共14张PPT）_人教新课标

八年级下数学课件：17-1 勾股定理 （共14张PPT）_人教新课标

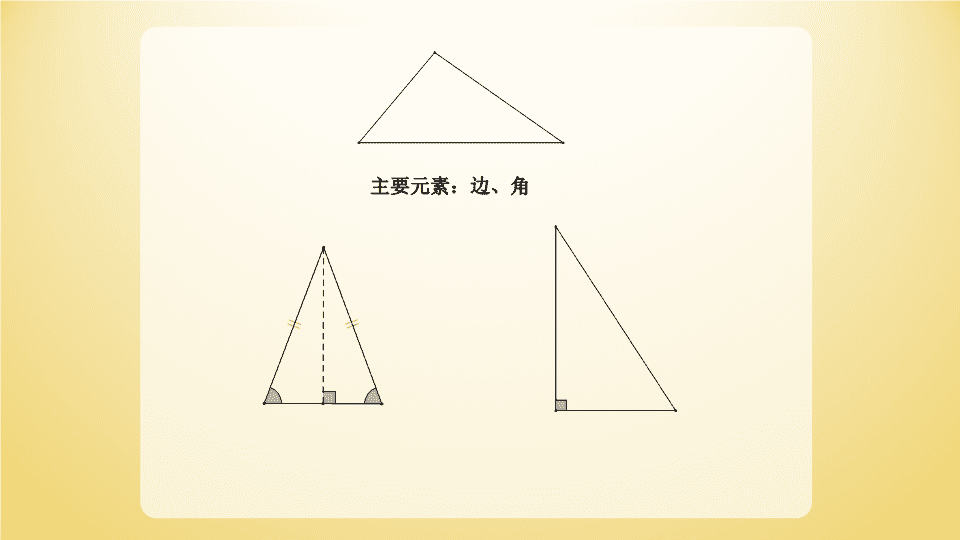
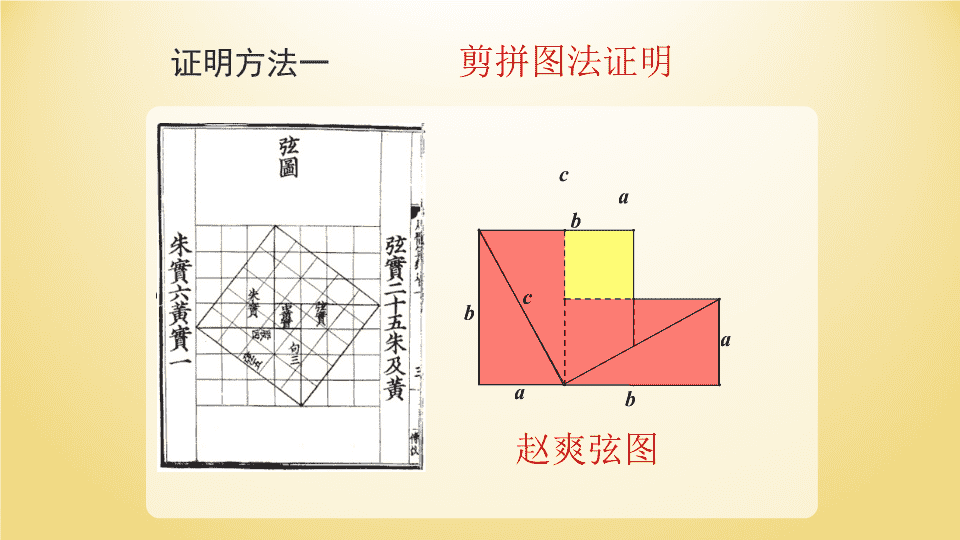
17.1勾股定理 主要元素：边、角 赵爽弦图证明方法一剪拼图法证明 勾股定理：如果直角三角形两条直角边长分别为a、b，斜边长为c，那么a2+b2=c2．aABC┏bc股勾 S大正方形＝S大正方形＝＝c2＋4×ab∴(a+b)2＝c2＋4×aba2+2ab+b2=c2+2ab∴a2+b2=c2(a+b)2S小正方形＋4S直角三角形证明方法二面积恒等法证明 毕达哥拉斯证法证明方法三 学以致用1.在RtΔABC中,∠C=90º①已知a=1,b=2,求c．②已知b=2,c=4,求a．2.在RtΔABC中,∠B=90º，已知a=2,b=5,求c．BAC42BAC21CAB25 3.在RtΔABC中，两条边的长度分别是3和4，求另一边的长度.分类讨论BAC43①斜边＝②直角边＝BAC34 4.如图，图中所有的三角形都是直角三角形，四边形都是正方形．已知正方形A，B，C，D的面积分别是3，4，1，3，求最大正方形E的面积．勾股树 公元前约3000年，古巴比伦人就知道和应用勾股定理，他们还知道许多勾股数组，如3,4,5．大约公元前2500年，古埃及人在建筑宏伟的金字塔和测量尼罗河泛滥后的土地时，也应用过勾股定理．大约公元前2000年，大禹在治水的实践中总结出了勾股术，用来确定两处水位的高低差．可以说，禹是世界上有史记载的第一位与勾股定理有关的人．大约在公元前1100年，周朝数学家商高就提出“勾三、股四、弦五”，记载在《周髀算经》中．公元前3世纪，古希腊数学家欧几里德巨著《几何原本》中给出一个勾股定理的证明．公元前5世纪，古希腊数学家毕达哥拉斯就公开发表了这一规律的证明．公元2世纪的东汉时期，刘徽证明了勾股定理．大约公元前250年，赵爽对《周髀算经》内的勾股定理作出了详细注释和证明．2002年在北京召开的国际数学家大会，就以赵爽弦图作为大会会徽的图案． 在探索勾股定理的过程中，你有什么感悟和欣赏. 如图，以直角三角形各边为直径向外作半圆，则半圆A，B，C的面积关系为根据勾股定理，，a2+b2=c2得到半圆A，B，C的面积关系为SA+SB=SC．圆的面积公式：,S=πr2数形结合放眼未来，华罗庚曾设想：向太空发射一种图形，因为这种图形在几千年前就已经被人类所认识，如果外星人是“文明人”，也必定认识这种图形. 从直角三角形的各边向外作正方形能否推广到从各边向外作等边三角形（正n边形）吗？ 作业：（1）整理课堂上所提到的勾股定理的证明方法；（2）教材28页，1、2、3（3）通过上网等方式查找勾股定理的有关史料、趣事及其他证明方法．