八年级上数学课件八年级上册数学课件《勾股定理的应用》 北师大版 (2)_北师大版

八年级上数学课件八年级上册数学课件《勾股定理的应用》 北师大版 (2)_北师大版

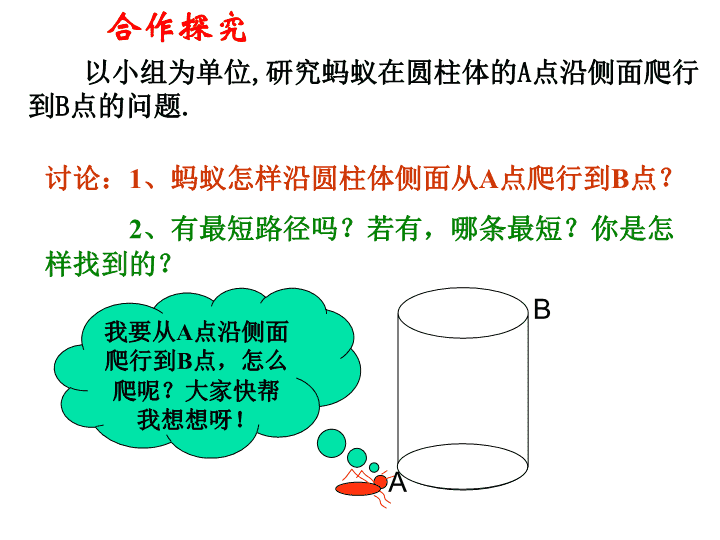
勾股定理的应用 在同一平面内，两点之间,线段最短情景导入从行政楼A点走到教学楼B点怎样走最近？教学楼行政楼BA你能说出这样走的理由吗？在同一平面内， 以小组为单位,研究蚂蚁在圆柱体的A点沿侧面爬行到B点的问题.合作探究讨论：1、蚂蚁怎样沿圆柱体侧面从A点爬行到B点？2、有最短路径吗？若有，哪条最短？你是怎样找到的？BA我要从A点沿侧面爬行到B点，怎么爬呢？大家快帮我想想呀！ 爬行路径：（1）（2）（3）（4）ABABABAB 例题1：如图所示，有一个圆柱，它的高是12cm,底面上圆的周长等于18cm，在圆柱下底面的点A处有一只蚂蚁，它想吃到上底面上与点A相对的点B处的食物，沿圆柱侧面爬行到B点，求其爬行的最短路程是多少？ 例题解析：C解：由题意得展开图，知线段AB即为最短路径，其中AC=12,BC=故,最短路径是15cm。转化BA 做一做李叔叔想要检测雕塑底座正面的AD边和BC边是否分别垂直于底边AB，但他随身只带了卷尺，（1）你能替他想办法完成任务吗？（2）李叔叔量得AD长是30厘米，AB长是40厘米，BD长是50厘米，AD边垂直于AB边吗？为什么？（3）小明随身只有一个长度为20厘米的刻度尺，他能有办法检验AD边是否垂直于AB边吗？BC边与AB边呢？ 如图是一个滑梯示意图，若将滑道AC水平放置，则刚好与AB一样长。已知滑梯的高度ＣＥ＝３ｍ，ＣＤ＝１ｍ，试求滑道ＡＣ的长例题2： 练一练：甲、乙两位探险者到沙漠进行探险，某日早晨8：00甲先出发，他以6km/h的速度向正东行走，1小时后乙出发，他以5km/h的速度向正北行走。上午10：00，甲、乙两人相距多远？解:如图:已知A是甲、乙的出发点，10:00甲到达B点,乙到达C点.则:AB=2×6=12(千米)AC=1×5=5(千米)在Rt△ABC中∴BC=13(千米)即甲乙两人相距13千米 拓展延伸：如左图的长方体，长方体底面长为2,宽为1,高为4,蚂蚁从A点沿长方体表面爬到E点有多少种爬行可能？那种爬行路径的距离最短？是多少？ 解：长方体侧面展开图一共有三种情况，如上图，其距离分别是：第一种：第二种：第三种：例题变式：DAGHFE241左上（1）BAGFHE241前上（2）ABCFGE412前右（3） 2、注意：运用勾股定理解决实际问题时，①、没有图的要按题意画好图并标上字母；②、有时必须设好未知数，并根据勾股定理列出相应的方程式才能做出答案。归纳总结1、数学思想：数学问题转化实际问题