北师大版数学八年级上册《平行线的性质》练习

北师大版数学八年级上册《平行线的性质》练习

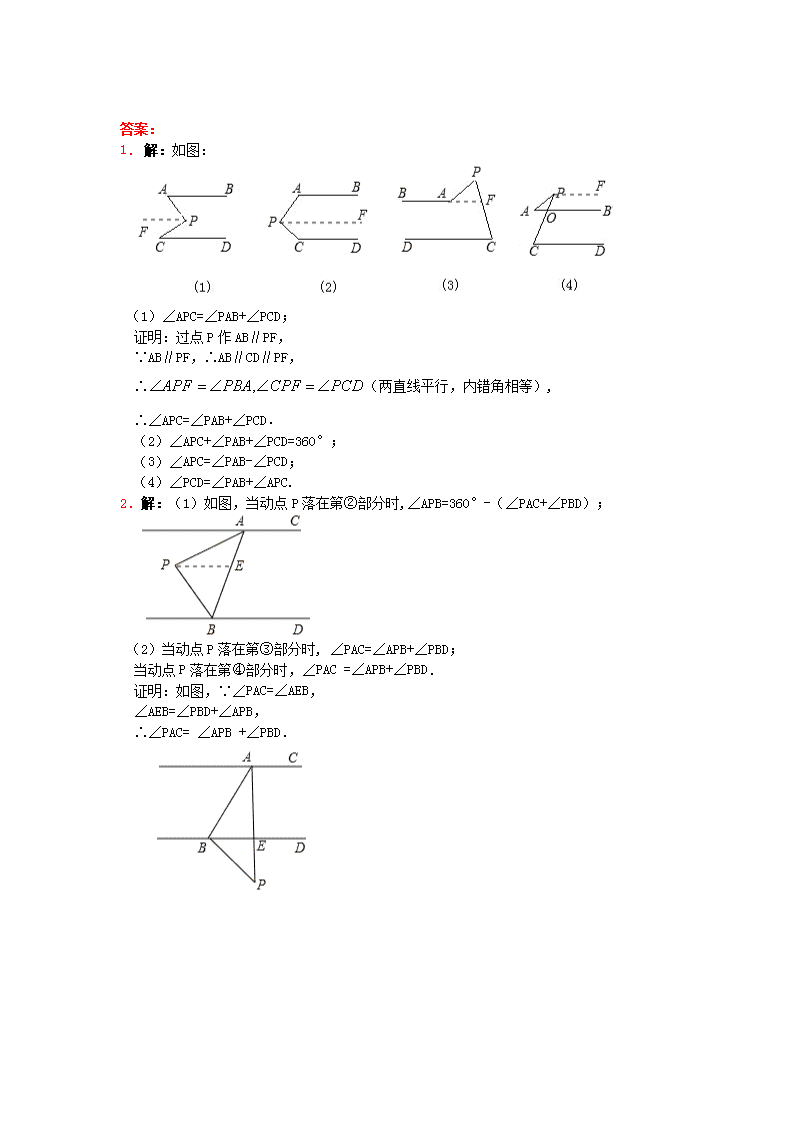
7.4平行线的性质专题与平行线有关的探究题1．如图，AB∥CD，分别探讨下面四个图形中∠APC与∠PAB、∠PCD的关系，请你从所得到的关系中任选一个加以说明．（适当添加辅助线，其实并不难）2．利用平行线的性质探究：如图，直线AC∥BD，连接AB，直线AC，BD及线段AB把平面分成①②③④四个部分，规定线上各点不属于任何部分．当动点P落在某个部分时，连接PA、PB，构成∠PAC、∠APB、∠PBD三个角．当动点P落在第①部分时，小明同学在研究∠PAC、∠APB、∠PBD三个角的数量关系时，利用图1，过点P作PQ∥BD，得出结论：∠APB=∠PAC+∠PBD．请你参考小明的方法解决下列问题：（1）当动点P落在第②部分时，在图2中画出图形，写出∠PAC、∠APB、∠PBD三个角的数量关系；（2）当动点P落在第③、第部分时，在图3、图4中画出图形，探究∠PAC、∠APB、∠PBD之间的数量关系，写出结论并选择其中一种情形加以证明． 答案：1．解：如图：（1）∠APC=∠PAB+∠PCD；证明：过点P作AB∥PF，∵AB∥PF，∴AB∥CD∥PF，∴（两直线平行，内错角相等）,∴∠APC=∠PAB+∠PCD．（2）∠APC+∠PAB+∠PCD=360°；（3）∠APC=∠PAB-∠PCD；（4）∠PCD=∠PAB+∠APC.2．解：（1）如图，当动点P落在第②部分时,∠APB=360°-（∠PAC+∠PBD）；（2）当动点P落在第③部分时,∠PAC=∠APB+∠PBD；当动点P落在第部分时，∠PAC=∠APB+∠PBD．证明：如图，∵∠PAC=∠AEB，∠AEB=∠PBD+∠APB，∴∠PAC=∠APB+∠PBD．