八年级上数学课件- 13-3-1 等腰三角形 课件（共21张PPT）_人教新课标

八年级上数学课件- 13-3-1 等腰三角形 课件（共21张PPT）_人教新课标

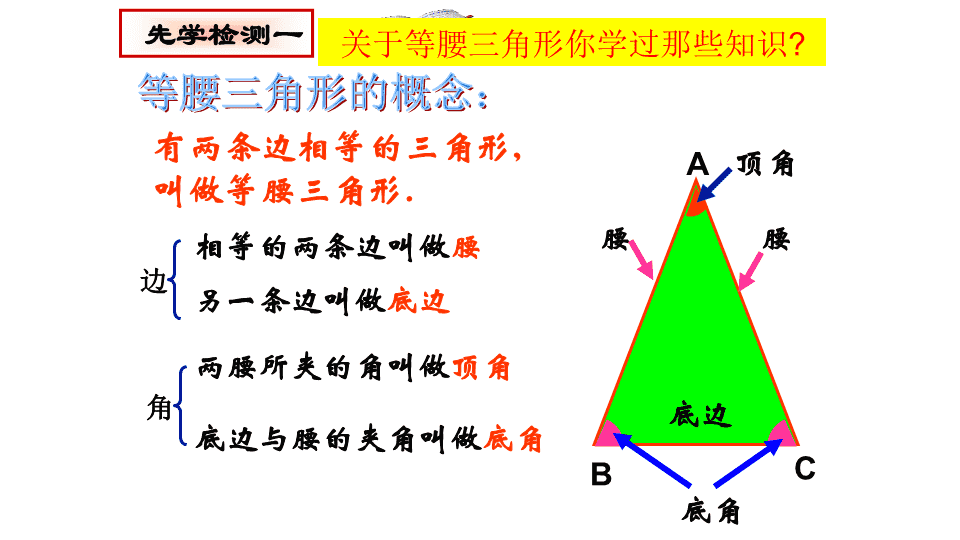
13.3.1等腰三角形 下载图片共同特点观赏寻找 ABC有两条边相等的三角形,叫做等腰三角形.等腰三角形的概念：相等的两条边叫做腰另一条边叫做底边底边与腰的夹角叫做底角两腰所夹的角叫做顶角腰腰底边顶角底角先学检测一关于等腰三角形你学过那些知识?边角 ABCAB=AC等腰三角形课前先学：心灵手巧探索新知材料:剪刀、一张矩形纸方法（1）先将矩形纸按图中虚线对折；（2）剪去阴影部分；（3）将剩余部分展开。 ACBD先学提示二：细心观察大胆猜想自主学习教科书75页内容，按要求完成下列学习任务（时间：5分钟）1、判断等腰三角形是轴对称图形吗？如果是请找出对称轴。2、把剪出的等腰三角形ABC沿折痕AD对折，找出其中重合的线段和角，独立完成大册子50页的表格。3、观察等腰三角形的两底角、顶角平分线、底边上的中线、底边上的高，你有什么发现？（小组讨论）4、请根据以上探究完成大册子50页等腰三角形性质的归纳。对称轴是底边上的高（顶角平分线或底边的中线）所在的直线 得出结论1等腰三角形的两个底角相等（简写成“等边对等角”）；作用：常用来证明两角相等，求等腰三角形各角的度数2等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合。（可简记为“三线合一”）作用：研究等腰三角形的有关问题时“三线”是常用的辅助线． 等腰三角形的两个底角相等已知：△ABC中，AB=AC求证：∠B=C分析：1.如何证明两个角相等？2.如何构造两个全等的三角形？论证ABCD3.你能想到几种方法？；（简写成“等边对等角”） 证明：作顶角的平分线AD.则有∠1＝∠2AB=AC(已知),∠1=∠2(辅助线作法)，AD=AD(公共边),∴△BAD≌△CAD(SAS).∴∠B=∠C(全等三角形的对应角相等).已知：△ABC中，AB=AC.求证：∠B=∠C.ABC12证明：等腰三角形的两个底角相等作顶角的平分线D方法一在△BAD和△CAD中， 证明：作底边中线AD则BD=CDAB=AC(已知),BD=CD(辅助线作法)，AD=AD(公共边),∴△BAD≌△CAD(SSS).∴∠B=∠C(全等三角形的对应角相等).已知：△ABC中，AB=AC.求证：∠B=∠C.ABCD证明：等腰三角形的两个底角相等作底边中线方法二在△BAD和△CAD中， 已知：△ABC中，AB=AC.求证：∠B=∠C.ABC证明：作底边高线AD.则有∠ADB＝∠ADC＝90ºAB=AC(已知),AD=AD(公共边),∴Rt△BAD≌Rt△CAD(HL).∴∠B=∠C(全等三角形的对应角相等).D证明：等腰三角形的两个底角相等作底边的高线在Rt△BAD和△RtCAD中，方法三 等腰三角形的性质1：等腰三角形的两个底角相等。性质1(等边对等角)ABCD结论几何语言在△ABC中∵AB=AC∴∠B=∠C D如图，作底边的中线AD.D如图作底边的高AD.D如图，作顶角的平分线AD.ABCABCABC等腰三角形常见的辅助线归纳提炼一： 等腰三角形的性质2：性质2ABCD结论等腰三角形的顶角平分线，底边上的中线，底边上的高互相重合。（等腰三角形的“三线合一”） D中线AD.D高AD.D顶角的平分线AD.ABCABCABC归纳提炼二：等腰三角形的三线知一线得二线∵AB=ACAD⊥BC,∴∠=∠,=;∵AB=ACBD=CD，∴⊥，∠=∠；∵AB=AC∠BAD=∠CAD∴⊥，=。符号语言：在△ABC中，BADCADBDCDBADCADADBCCDADBCBD 例：如图，在△ABC中，AB=AC，点D在AC上，且BD=BC=AD，求△ABC各角的度数。ABCDx⌒2x⌒2x⌒⌒2x解：∵AB=AC，BD=BC=AD，∴∠ABC==，∠A=（)设∠A=x,则∠BDC==从而==∠BDC=于是在△ABC中，有∠A+∠ABC+∠C==解得x=，在△ABC中，∠A=，∠ABC=∠C=∠C∠BDC∠ABD等边对等角∠A+∠ABD2x,∠ABC2x,∠C36°180°x+2x+2x72°36° 1.等腰三角形一个底角为70°,它的顶角为______.2.等腰三角形一个角为70°,它的另外两个角为__________________.3.等腰三角形一个角为110°,它的另外两个角为_______.40°35°，35°70°,40°或55°,55°归纳提炼:在等腰三角形中,①1顶角度数+2×底角度数=180°②0°＜顶角度数＜180°③0°＜底角度数＜90°达标检测 能力提升1.在三角形ABC中，AB=AC，且AD⊥BC，已知BD=2cm,求DC=___cm,BC=___cm？CBDA12∵AB=AC,AD⊥BC（已知）∴BD=CD（等腰三角形的高与底边上的中线重合）即（等腰三角形三线合一）∵BD=2cm（已知）∴CD=2cmBC=4cm24 2．等腰三角形一腰上的高与另一腰的夹角为60°，则这个等腰三角形的顶角为（）A．30°B．150°C．30°或150°D．120°C 3.如图，在等腰三角形ABC中，AB=AC，D为BC的中点，则点D到AB，AC的距离相等。请说明理由。┐┐AEFBDC解：相等，理由如下：连接AD在△ABC中，∵AB=AC，D为ＢC中点∴AD平分∠BAC∵DE⊥AB，DF⊥AC∴DE=DF 小结归纳通过本节课的学习，你有哪些收获？对称轴是底边上的高（顶角平分线或底边的中线）所在的直线 谢谢！课后作业:课本P81页习题13.3第1题