八年级下数学课件：18-1-2 平行四边形的判定 （共24张PPT）_人教新课标

八年级下数学课件：18-1-2 平行四边形的判定 （共24张PPT）_人教新课标

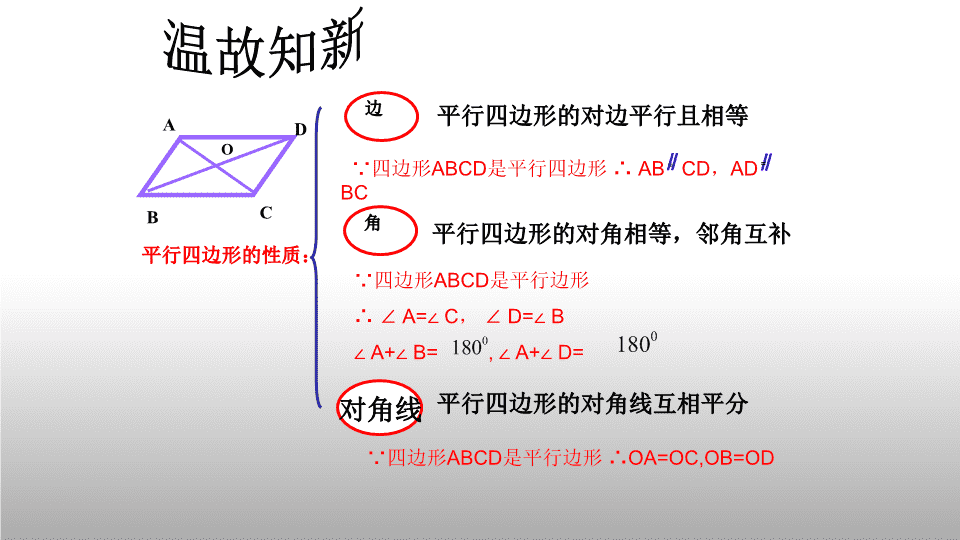
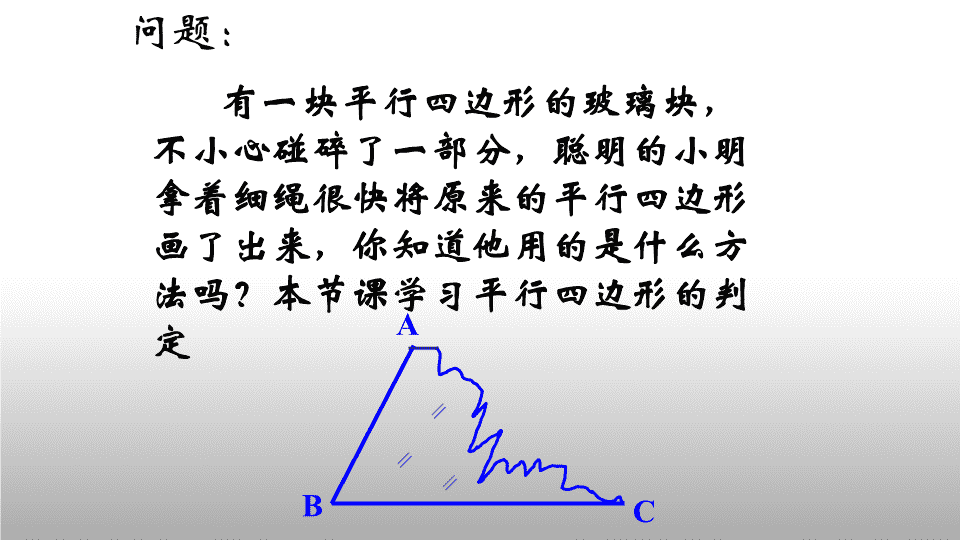
18.1.2平行四边形的判定 边平行四边形的对边平行且相等角对角线平行四边形的对角线互相平分温故知新平行四边形的性质：BDACO∵四边形ABCD是平行四边形∴ABCD，ADBC∥﹦∥﹦平行四边形的对角相等，邻角互补∵四边形ABCD是平行边形∴∠A=∠C，∠D=∠B∠A+∠B=,∠A+∠D=∵四边形ABCD是平行边形∴OA=OC,OB=OD 有一块平行四边形的玻璃块，不小心碰碎了一部分，聪明的小明拿着细绳很快将原来的平行四边形画了出来，你知道他用的是什么方法吗？本节课学习平行四边形的判定问题：ABC 到底何为平行四边形？定义判定法：两组对边分别平行的四边形是平行四边形。ABCD∵AB∥CD，AD∥BC（已知）∴四边形ABCD是平行四边形（两组对边分别平行的四边形是平行四边形。）数学语言表示为： 从平行四边形的性质逆向思考　提出猜想两组对边分别相等的四边形是平行四边形平行四边形的性质逆命题平行四边形的两组对边分别相等平行四边形的两组对角分别相等平行四边形的对角线互相平分两组对角分别相等的四边形是平行四边形对角线互相平分的四边形是平行四边形思考：判定这些逆命题的真假？ 已知：如图，在四边形ABCD中，AB=CD，AD=BC．求证：四边形ABCD是平行四边形．演绎推理　形成定理两组对边分别相等的四边形是平行四边形．判定定理1DABC1234 ABCD∵AB＝CD，AD＝BC（已知）∴四边形ABCD是平行四边形（两组对边分别相等的四边形是平行四边形）平行四边形判定平行四边形的判定定理1：两组对边分别相等的四边形是平行四边形。符号语言： 小试牛刀DABCEF证明：四边形ABCD是平行四边形AD∥BC且AD=BCEAD=FCBAE=CFEAD=FCBAD=BCAED≌CFB(SAS)DE=BF四边形BFDE是平行四边形在AED和CFB中同理可证：BE=DF已知：E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF。求证：四边形BFDE是平行四边形 证明：∵　多边形ABCD是四边形，∴∠A+∠B+∠C+∠D=360°．又∵∠A=∠C，∠B=∠D，∴∠A+∠B=180°，∠B+∠C=180°．∴AD∥BC，AB∥DC．∴四边形ABCD是平行四边形．已知：如图，在四边形ABCD中，∠A=∠C，∠B=∠D．求证：四边形ABCD是平行四边形．演绎推理　形成定理两组对角分别相等的四边形是平行四边形．判定定理2猜想2DABC 已知：如图，在四边形ABCD中，AC，BD相交于点O，且OA=OC，OB=OD．求证：四边形ABCD是平行四边形．演绎推理　形成定理对角线互相平分的四边形是平行四边形．判定定理3DABCO猜想3证明：∵OA=OC，OB=OD，∠AOD=∠COB，∴△AOD≌△COB（SAS）∴∠OAD=∠OCB∴AD∥BC同理AB∥DC∴四边形ABCD是平行四边形． 平行四边形的判定定理：1.两组对边分别相等的四边形是平行四边形。两组对角分别相等的四边形是平行四边形。对角线互相平分的四边形是平行四边形。2.3.总结 请你识别下列四边形哪些是平行四边形?请说明理由？ADCB110°70°110°（1）（3）（2）ABCDO5㎝5㎝4㎝4㎝BADC4.8㎝4.8㎝7.6㎝7.6㎝夯实基础 例:已知,平行四边形ABCD对角线AC,BD相较于点O,E、F是AC上的两点，并且E是OA的中点，F是OC的中点.大显身手求证：四边形BFDE是平行四边形. 变式1：已知平行四边形ABCD对角线AC,BD相较于点O,E、F是平行四边形ABCD对角线AC上的两点，并且AE=CF.求证：四边形BFDE是平行四边形改一改，证一证（一） 变式2：已知平行四边形ABCD对角线AC,BD相较于点O,E、F是平行四边形ABCD对角线AC上的任意两点.四边形BFDE是平行四边形吗？为什么？改一改，证一证（二） 同学们现在想想看，你们有没有办法把原来的平行四边形重新画出来？再回到课前问题1：ABC 方法（一）DABC两组对边分别平行的四边形是平行四边形 方法（二）DABC两组对边分别相等的四边形是平行四边形 方法（三）DABC两组对角分别相等的四边形是平行四边形 方法（四）DOABC对角线互相平分的四边形是平行四边形 DCAB平行四边形的判定定理:O小结两组对边分别相等的四边形是平行四边形；对角线互相平分的四边形是平行四边形；两组对角分别相等的四边形是平行四边形。定义：两组对边分别平行的四边形是平行四边形平行四边形的判定方法 P50习题18.1第4.5.13题作业：写调查小报告《生活中平行四边形研究》 FADBCE更上一层楼1.如图，在ABCD中，已知AE、CF分别是∠DAB、∠BCD的角平分线，61234785求证：四边形AECF是平行四边形。 2.如图，在△ABC中，BD平分∠ABC,DE∥BC交AB于点E,EF∥AC交BC于点F。试判断BE与CF的数量关系，并说明理由。AEDBFC