八年级上数学课件八年级上册数学课件《平行线的性质》 北师大版 (10)_北师大版

八年级上数学课件八年级上册数学课件《平行线的性质》 北师大版 (10)_北师大版

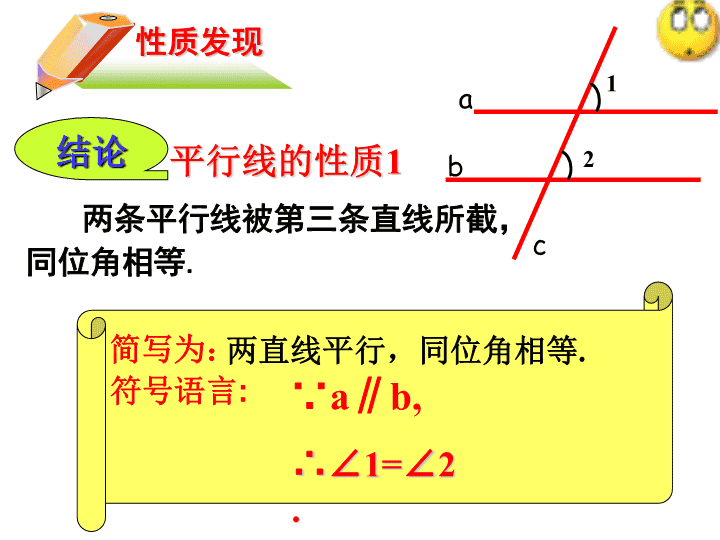
平行线的性质学习目标理解并掌握平行线性质定理的推导会用平行线的性质进行推理和计算。 复习回顾两直线平行1、同位角相等2、内错角相等3、同旁内角互补平行线的判定方法是什么？ 两直线平行，同位角相等.平行线的性质1结论两条平行线被第三条直线所截，同位角相等.性质发现∴∠1=∠2.∵a∥b,简写为：符号语言:b12ac 如图：已知a//b,那么2与3相等吗？为什么?解∵a∥b(已知),∴∠1=∠2(两直线平行,同位角相等).又∵∠1=∠3(对顶角相等),∴∠2=∠3(等量代换).合作交流一b12ac3 两直线平行，内错角相等.平行线的性质2结论两条平行线被第三条直线所截，内错角相等.性质发现∴∠2=∠3.∵a∥b,符号语言:简写为：b12ac3 解：∵a//b（已知）,如图,已知a//b,那么2与4有什么关系呢？为什么?合作交流二b12ac4∴1=2（两直线平行，同位角相等）.∵1+4=180°（邻补角定义）,∴2+4=180°（等量代换）. 两直线平行，同旁内角互补.平行线的性质3结论两条平行线被第三条直线所截，同旁内角互补.性质发现∴2+4=180°.∵a∥b,符号语言:简写为：b12ac4 如果两条直线都和第三条直线平行，那么这两条直线也互相平行。例已知：如图，直线a,b,c被直线d所截，且a∥b,c∥b，∠1，∠2和∠3,是直线a、b,c被直线d截出的同位角求证：a∥cabcd.师生互动,典例示范证明:∵b∥a,(已知）∴∠1=∠2,（两直线平行，同位角相等）∵c∥a（已知）∴∠3=∠1两直线平行，同位角相等）∴∠2=∠3（等量代换）∴b∥c（同位角相等，两直线平行） 1如图,已知直线a∥b,∠1=500,求∠2的度数.abc12∴∠2=500(等量代换).解：∵a∥b(已知),∴∠1=∠2(两直线平行,内错角相等).又∵∠1=500(已知),变式１：已知条件不变，求∠3，∠4的度数？3三施展你的才能4 变式2:已知∠3=∠4，∠1=47°,求∠2的度数？∴∠2=470（）解：∵∠3=∠4()∴a∥b()又∵∠1=470()c1234abd两直线平行，同位角相等同位角相等,两直线平行已知已知 2如图在四边形ABCD中,已知AB∥CD,∠B=600.①求∠C的度数;②由已知条件能否求得∠A的度数?ABCD解:①∵AB∥CD(已知),∴∠B+∠C=1800(两直线平行,同旁内角互补).又∵∠B=600(已知),∴∠C=1200(等式的性质).②根据题目的已知条件,无法求出∠A的度数. 两直线平行同位角相等内错角相等同旁内角互补线的关系角的关系判定性质平行线的性质和平行线的判定方法的区别与联系小结 平行线的性质由“线”定“角”由“角”定“线”平行线的判定