八年级数学上册第一章勾股定理本章归纳总结课件 北师大版

八年级数学上册第一章勾股定理本章归纳总结课件 北师大版

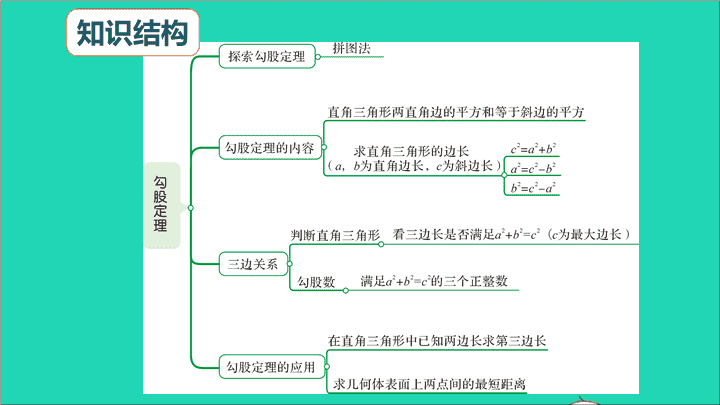
本章归纳总结 知识结构 释疑解惑，加深理解1.勾股定理的证明：勾股定理的证明方法有多种，一般是采用剪拼的方法，它把“数与形”巧妙地联起来，是几何体与代数沟通的桥梁，同时也为后面的四边形、圆、图形交换，三角函数等的互化的学习提供了方法和依据。 2.勾股定理中的分类讨论在勾股定理的写法运用中，如果不说明给出直角三角形中有两条边的长，要求第三条边的长就需要分两种情况讨论，即第一种情况是告诉两条直角边长求斜边，第二种情况是告诉一条直角边和斜边长求另一条直角边。 3.曲面两点间的距离问题在解决曲面中两点间的距离时，往往是要将曲面问题转化为同一平面内两点之间的距离，这是解决问题的关键. 例1：如图所示，在平面直角会标系中，点P的坐标为(-2，3)，以点O为圆心，以OP的长为半径画弧，交x轴的负半轴于点A，则点A的横坐标介于()A.-4和-3之间B.3和4之间C.-5和-4之间D.4和5之间典例精析，复习新知 例2在△ABC中，AB=2，BC=1，∠ABC=45°以AB为一边作等腰直角三角形ABD，使∠ABD=90°，连接CD，则线段CD的长为。 例3一张直角三角形纸片，两直角边AC=6cm，BC=8cm，将△ABC折叠，使点B与点A重合，折痕是DE（如图所示），求CD的长.分析：设CD为x，∵AD=BD，∴AD=8-x.∴在△ACD中，根据勾股定理列出关于x的方程即可求解. 例4有一个立方体礼盒如图所示，在底部A处有一只壁虎，C′处有一只蚊子，壁虎急于捕捉到蚊子充饥.（1）试确定壁虎所走的最短路线；（2）若立方体礼盒的棱长为20cm，则壁虎如果想在半分钟内捕捉到蚊子，每分钟至少要爬行多少厘米？（保留整数）分析：求几何表面的最短距离时，通常可以将几何体表面展开，把立体图形转化为平面图形. 复习训练，巩固提高