- 2022-04-01 发布 |
- 37.5 KB |
- 119页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
人教版八年级下册数学期中、期末试题及答案,精品20套
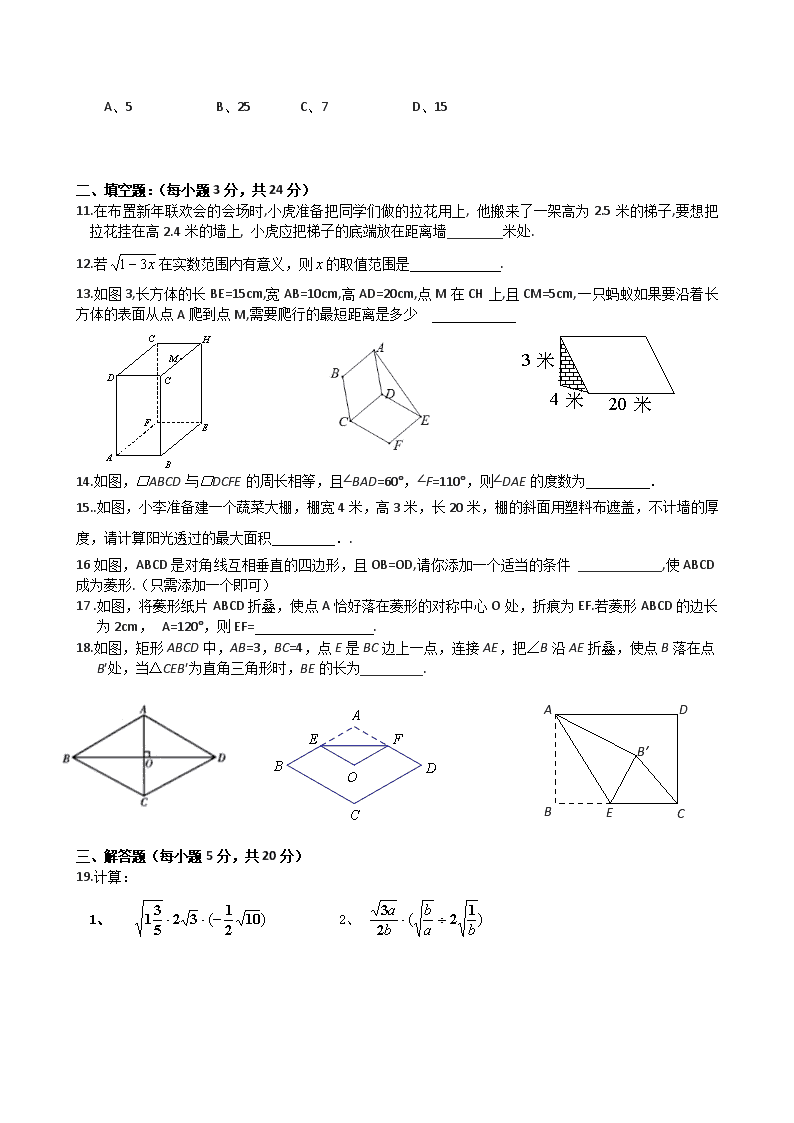
人教版八年级下册数学期中、期末试题及答案,精品20套八年级下册数学期中考试题一、选择题(每小题2分,共12分)1.下列式子中,属于最简二次根式的是()A.B.C.D.2.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D.2题图4题图3.若代数式有意义,则实数的取值范围是()A.≠1B.≥0C.>0D.≥0且≠14如图字母B所代表的正方形的面积是()A.12B.13C.144D.1945.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.D.6如图4为某楼梯,测得楼梯的长为5米,高3米,计划在楼梯表面铺地毯,地毯的长度至少需要多少米?A4B8C9D77三角形的三边长分别为6,8,10,它的最短边上的高为()A.6B.4.5C.2.4D.88.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5º,EF⊥AB,垂足为F,则EF的长为()A.1B.C.4-2D.3-49.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是()A.1:2:3:4B.1:2:2:1C.1:2:1:2D.1:1:2:210已知x、y为正数,且│x2-4│+(y2-3)2=0,如果以x、y的长为直角边作一个直角三角形,那么以这个直角三角形的斜边为边长的正方形的面积为() A、5B、25C、7D、15二、填空题:(每小题3分,共24分)11.在布置新年联欢会的会场时,小虎准备把同学们做的拉花用上,他搬来了一架高为2.5米的梯子,要想把拉花挂在高2.4米的墙上,小虎应把梯子的底端放在距离墙________米处.12.若在实数范围内有意义,则的取值范围是.13.如图3,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少14.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数为.15..如图,小李准备建一个蔬菜大棚,棚宽4米,高3米,长20米,棚的斜面用塑料布遮盖,不计墙的厚度,请计算阳光透过的最大面积..16如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件____________,使ABCD成为菱形.(只需添加一个即可)17.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,∠A=120°,则EF=.18.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_________.ECDBAB′三、解答题(每小题5分,共20分)19.计算:1、2、 20.如图,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.16题图21.先化简,后计算:,其中,.22.如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?23.在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.(1)求证:四边形BFDE为平行四边形;(2)若四边形BFDE为菱形,且AB=2,求BC的长.19题图ABCDNMP24.如图,在四边形ABCD中,AB=BC,对角线BD平分ÐABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。(1)求证:ÐADB=ÐCDB;(2)若ÐADC=90°,求证:四边形MPND是正方形。 25.如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连结DE,CF。(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长。21题图26.如图,是一块由边长为20cm的正方形地砖铺设的广场,一只鸽子落在点A处,它想先后吃到小朋友撒在B、C处的鸟食,则鸽子至少需要走多远的路程?27.如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.(1)求证:DE=EF;(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.23题图28.如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。(1)求证;OE=OF; (2)若BC=,求AB的长。29.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.25题图30.如图,在等边三角形ABC中,BC=6cm.射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)填空:①当t为_________s时,四边形ACFE是菱形;②当t为_________s时,以A、F、C、E为顶点的四边形是直角梯形.26题图 参考答案1.B;2.C;3.D;4C5.D;6B7D8.C;9.C;10C110.7;12.≤;1325;14.25°;15.100平方米;16.OA=OC或AD=BC或AD∥BC或AB=BC;17.;18.或3;1920.解:∵四边形ABCD是菱形,对角线AC与BD相交于O,∴AC⊥BD,DO=BO,∵AB=5,AO=4,∴BO==3,∴BD=2BO=2×3=6.21.:原式当,时,原式的值为。22.由条件可以推得FC=4,利用勾股定理可以得到EC=3cm.23.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD,∴∠ABD=∠CDB,∵在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,∴∠ABE=∠EBD=∠ABD,∠CDF=∠CDB,∴∠ABE=∠CDF,在△ABE和△CDF中∴△ABE≌△CDF(ASA),∴AE=CF,∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴DE=BF,DE∥BF, ∴四边形BFDE为平行四边形;(2)解:∵四边形BFDE为为菱形,∴BE=ED,∠EBD=∠FBD=∠ABE,∵四边形ABCD是矩形,∴AD=BC,∠ABC=90°,∴∠ABE=30°,∵∠A=90°,AB=2,∴AE==,BE=2AE=,∴BC=AD=AE+ED=AE+BE=+=2.24.(1)∵BD平分ÐABC,∴ÐABD=ÐCBD。又∵BA=BC,BD=BD,∴△ABD@△CBD。∴ÐADB=ÐCDB。(4分)(2)∵PM^AD,PN^CD,∴ÐPMD=ÐPND=90°。又∵ÐADC=90°,∴四边形MPND是矩形。∵ÐADB=ÐCDB,PM^AD,PN^CD,∴PM=PN。∴四边形MPND是正方形。25.(1)略(2)26.AB=5cm,BC=13cm.所以其最短路程为18cm27.解答:证明:(1)∵DE∥BC,CF∥AB,∴四边形DBCF为平行四边形,∴DF=BC,∵D为边AB的中点,DE∥BC,∴DE=BC,∴EF=DF﹣DE=BC﹣CB=CB,∴DE=EF;(2)∵四边形DBCF为平行四边形,∴DB∥CF,∴∠ADG=∠G,∵∠ACB=90°,D为边AB的中点,∴CD=DB=AD,∴∠B=∠DCB,∠A=∠DCA,∵DG⊥DC,∴∠DCA+∠1=90°,∵∠DCB+∠DCA=90°, ∴∠1=∠DCB=∠B,∵∠A+∠ADG=∠1,∴∠A+∠G=∠B.28.(1)证明:∵四边形ABCD是矩形∴AB∥CD,∠OAE=∠OCF,∠OEA=∠OFC∵AE=CF∴△AEO≌△CFO(ASA)∴OE=OF(2)连接BO∵OE=OF,BE=BF∴BO⊥EF且∠EBO=∠FBO∴∠BOF=900∵四边形ABCD是矩形∴∠BCF=900又∵∠BEF=2∠BAC,∠BEF=∠BAC+∠EOA∴∠BAC=∠EOA∴AE=OE∵AE=CF,OE=OF∴OF=CF又∵BF=BF∴△BOF≌△BCF(HL)∴∠OBF=∠CBF∴∠CBF=∠FBO=∠OBE∵∠ABC=900∴∠OBE=300∴∠BEO=600∴∠BAC=300∴AC=2BC=,∴AB=29(1)证明:∵Rt△OAB中,D为OB的中点,∴DO=DA,∴∠DAO=∠DOA=30°,∠EOA=90°,∴∠AEO=60°,又∵△OBC为等边三角形,∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴CO∥AB,∴四边形ABCE是平行四边形;(2)解:设OG=x,由折叠可得:AG=GC=8﹣x,在Rt△ABO中,∵∠OAB=90°,∠AOB=30°,BO=8, AO=,在Rt△OAG中,OG2+OA2=AG2,x2+(4)2=(8﹣x)2,解得:x=1,∴OG=1.30.(1)证明:∵∴∵是边的中点∴又∵∴△ADE≌△CDF(2)①∵当四边形是菱形时,∴由题意可知:,∴②若四边形是直角梯形,此时过作于M,,可以得到,即,∴,此时,重合,不符合题意,舍去。若四边形若四边形是直角梯形,此时,∵△ABC是等边三角形,F是BC中点,∴,得到经检验,符合题意。 ∴①②初中数学八年级下期中试题一、选择题(每小题4分,共32分)1.下列式子中,属于最简二次根式的是()AB.C.D.2.x为何值时,在实数范围内有意义()A、x>1B、x≥1C、x<1D、x≤1.3.已知a,b,c为△ABC三边,且满足(a2-b2)(a2+b2-c2)=0,则它的形状为( )A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形4.x<2,化简+|3-x|的结果是()A、-1B、1C、2x-5D、5-2x5.直角三角形中一直角边的长为9,另两边为连续自然数,则直角三角形的周长为( )A.121B.120C.90D.不能确定7题图6题图6.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.D.7.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5º,EF⊥AB,垂足为F,则EF的长为()A.1B.C.4-2D.3-48.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是()A.1:2:3:4B.1:2:2:1C.1:2:1:2D.1:1:2:2 二、填空题:(每小题3分,共15分)9.计算:÷=_______。ACB10..如图,已知中,,,,以直角边为直径作半圆,则这个半圆的面积是....11.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件____________,使ABCD成为菱形.(只需添加一个即可)12..如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,∠A=120°,则EF=.13..如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_________.ECDBAB′13题图11题图12题图三、解答题14、(4分)计算:(-)-(2-) 15(5分)..先化简,后计算:.,其中,16.(5分)有一个直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿∠CAB的角平分线AD折叠,使它落在斜边AB上,且与AE重合,你能求出CD的长吗?17题图ABCDNMP17.(9分)如图,在四边形ABCD中,AB=BC,对角线BD平分ABC,P是BD上一点,过点P作PMAD,PNCD,垂足分别为M、N。(1)求证:角ADB=角CDB;(2)若ADC=90,求证:四边形MPND是正方形。18题图18.(9分)如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连结DE,CF。(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长。 19题图19.(9分)如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.(1)求证:DE=EF;(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC.20.(12分)如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。(1)求证;OE=OF;(2)若BC=,求AB的长。 参考答案1.B;2.A;3.D;4.D;5.C;6.D;7C,8C9.;10.81Π/811OA=OC或AD=BC或AD∥BC或AB=BC;13.;13.或3;14.15:原式当,时,原式的值为。16.17.(1)∵BD平分ABC,∴ABD=CBD。又∵BA=BC,BD=BD,∴△ABD△CBD。∴ADB=CDB。(4分)(2)∵PMAD,PNCD,∴PMD=PND=90。又∵ADC=90,∴四边形MPND是矩形。∵ADB=CDB,PMAD,PNCD,∴PM=PN。∴四边形MPND是正方形。18证明:(1)∵四边形ABCD是平行四边形,∴DC∥AB,∴∠CDE=∠AED,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠ADE=∠AED,∴AE=AD,同理CF=CB,又AD=CB,AB=CD, ∴AE=CF,∴DF=BE,∴四边形DEBF是平行四边形,∴DE=BF,(2)△ADE≌△CBF,△DFE≌△BEF.19解答:证明:(1)∵DE∥BC,CF∥AB,∴四边形DBCF为平行四边形,∴DF=BC,∵D为边AB的中点,DE∥BC,∴DE=BC,∴EF=DF﹣DE=BC﹣CB=CB,∴DE=EF;(2)∵四边形DBCF为平行四边形,∴DB∥CF,∴∠ADG=∠G,∵∠ACB=90°,D为边AB的中点,∴CD=DB=AD,∴∠B=∠DCB,∠A=∠DCA,∵DG⊥DC,∴∠DCA+∠1=90°,∵∠DCB+∠DCA=90°,∴∠1=∠DCB=∠B,∵∠A+∠ADG=∠1,∴∠A+∠G=∠B.20.(1)证明:∵四边形ABCD是矩形∴AB∥CD,∠OAE=∠OCF,∠OEA=∠OFC∵AE=CF∴△AEO≌△CFO(ASA)∴OE=OF (2)连接BO∵OE=OF,BE=BF∴BO⊥EF且∠EBO=∠FBO∴∠BOF=900∵四边形ABCD是矩形∴∠BCF=900又∵∠BEF=2∠BAC,∠BEF=∠BAC+∠EOA∴∠BAC=∠EOA∴AE=OE∵AE=CF,OE=OF∴OF=CF又∵BF=BF∴△BOF≌△BCF(HL)∴∠OBF=∠CBF∴∠CBF=∠FBO=∠OBE∵∠ABC=90度∴∠OBE=30度∴∠BEO=60度∴∠BAC=30度∴AC=2BC=,∴AB=八年级下册数学期中测试卷一、选择题1、下列二次根式中,属于最简二次根式的是( )A.B.C. D.2、()A.x>3B.x>-3C.x≥-3D.x≥33、下列命题中,正确的个数是()ABCDE①若三条线段的比为1:1:,则它们组成一个等腰直角三角形;②两条对角线相等的平行四边形是矩形;③对角线互相平分且相等的四边形是矩形;④两个邻角相等的平行四边形是矩形;A、1个B、2个C、3个D、4个4、如图,在□ABCD中,已知AD=5cm,AB=3cm,AE平分∠BAD交BC边于点E,则EC等于()ABCDFD’(A)1cm(B)2cm(C)3cm(D)4cm5、如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D’处,则重叠部分△AFC的面积为().A.6B.8C.10D.126.下列各组数中,以a、b、c为边的三角形不是直角三角形的是()A.B.C.D.二、填空7、ABCD中一条对角线分∠A为35°和45°,则∠B=__度。8、矩形的两条对角线的夹角为600,较短的边长为12cm,则对角线的长↑↓←→为__________cm.9.如图由于台风的影响,一棵树在离地面处折断, 树顶落在离树干底部处,则这棵树在折断前(不包括树根)长度是.10、在平面直角坐标系中,点A(-1,0)与点B(0,2)的距离是_______。11、如图,每个小正方形的边长为1.在ABC中,点D为AB的中点,则线段CD的长为;O(A)BCD13.如图,在平面直角坐标系中,ABCD的顶点A、B、D的坐标分别是(0,0),(5,0)(2,3),则顶点C的坐标是()A.(3,7)B.(5,3)C.(7,3)D.(8,2)14、观察下列各式:请你找出其中规律,并将第n(n≥1)个等式写出来.三、解答题15、16.17、如图,已知□ABCD中,AE平分∠BAD,CF平分∠BCD,分别交BC、AD于E、F.求证:AF=EC证明: 18、已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).(1)四边形EFGH的形状是,证明你的结论.(2)连接四边形ABCD的对角线AC与BD,当AC与BD满足条件时,四边形EFGH是矩形;证明你的结论.19、已知:如图,中,,点D、E分别是AC、AB的中点,点F在BC的延长线上,且.求证:四边形DECF是平行四边形.证明: 最新人教版八年级下册数学期中测试题一、选择题(每题3分,共30分)1.下列根式中属最简二次根式的是( )A.B.C.D.2.设a=-1,a在两个相邻整数之间,则这两个整数是()A.1和2B.2和3C.3和4D.4和53.已知a<b,化简二次根式的正确结果是()A.B.C.D.4、等边三角形的边长为2,则该三角形的面积为()A:B:C:D:35、已知a、b、c是三角形的三边长,如果满足,则三角形的形状是()A:底与边不相等的等腰三角形B:等边三角形C:钝角三角形D:直角三角形6、若中,,高AD=12,则BC的长为()A:14B:4C:14或4D:以上都不对7.能判定四边形ABCD为平行四边形的题设是()(A)AB∥CD,AD=BC(B)AB=CD,AD=BC(C)∠A=∠B,∠C=∠D(D)AB=AD,CB=CD8.菱形和矩形一定都具有的性质是( )A、对角线相等 B、对角线互相垂直 C、对角线互相平分且相等 D、对角线互相平分9.如图,过矩形ABCD的四个顶点作对角线AC,BD的平行线,分别相交于E,F,G,H四点,则四边形EFGH为( )A.平行四边形B.矩形[来*C.菱形D.正方形10.已知,则的值为()A.B.8C.D.6二、填空题(每题4分,共24分)11.如果最简二次根式与是同类二次根式,那么.12、如图所示,以直角三角形ABC的三边向外作正方形,其面积分别为,且;13、如图,已知一根长8m的竹杆在离地3m处断裂,竹杆顶部抵着地面,此时,顶部距底部有m; 第12题第13题第14题第15题14.如图菱形ABCD的边长是2cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为________cm2. 15.如图,▱ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24厘米,△OAB的周长是18厘米,则EF= 厘米.16.如图,在正方形ABCD中,E是AB上一点,BE=2,AE=3BE,P是AC上一动点,则PB+PE的最小值是 .新课标第一网三.解答题(每题5分,共15分)17.先化简,再求值:,其中.18、在△ABC中,∠C=90°.(1)已知c=25,b=15,求a;(2)已知a=,∠A=60°,求b、c.19.如图,BD是菱形ABCD的对角线,点E,F分别在边CD,DA上,且CE=AF.求证:BE=BF.四、解答题每题8分,共24分)20、如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长? ABDCFE21.已知:如图所示,△ABC中,E、F、D分别是AB、AC、BC上的点,且DE∥AC,DF∥AB,要使四边形AEDF是菱形,在不改变图形的前提下,你需添加的一个条件是_______________试证明:这个多边形是菱形.22.如图,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.(1)试判断四边形OCED的形状,并说明理由;(2)若AB=6,BC=8,求四边形OCED的面积.五、解答题(每题9分,共27分)23.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.(1)求证:四边形AEBD是矩形.(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.24.细心观察图,认真分析各式,然后解答问题:O+1=2= +1=3=+1=4=(1)用含有n(n是正整数)的等式表示上述变化的规律;(2)推算出O的长;(3)求出+++…+的值。25.梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,AB=8cm,BC=26cm,动点P从点A开始,沿AD边,以1厘米/秒的速度向点D运动;动点Q从点C开始,沿CB边,以3厘米/秒的速度向B点运动。已知P、Q两点分别从A、C同时出发,,当其中一点到达端点时,另一点也随之停止运动。假设运动时间为t秒,问:(1)t为何值时,四边形PQCD是平行四边形?(2)在某个时刻,四边形PQCD可能是菱形吗?为什么?(3)四边形PQCD可能是矩形吗?不需要证明过程。新人教版八年级下数学期中考试题及答案一、选择题(每小题2分,共12分)1.下列式子中,属于最简二次根式的是()A.B.C.D.2.如图,在矩形ABCD中,AD=2AB,点M、N分别在边AD、BC上,连接BM、DN.若四边形MBND是菱形,则等于()A.B.C.D. 2题图4题图5题图3.若代数式有意义,则实数的取值范围是()A.≠1B.≥0C.>0D.≥0且≠14.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12B.24C.D.5.如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5º,EF⊥AB,垂足为F,则EF的长为()A.1B.C.4-2D.3-46.在平行四边形ABCD中,∠A:∠B:∠C:∠D的值可以是()A.1:2:3:4B.1:2:2:1C.1:2:1:2D.1:1:2:2二、填空题:(每小题3分,共24分)10题图7.计算:=.8.若在实数范围内有意义,则的取值范围是.9.若实数、满足,则=.10.如图,□ABCD与□DCFE的周长相等,且∠BAD=60°,∠F=110°,则∠DAE的度数书为.11.如图,在直角坐标系中,已知点A(﹣3,0)、B(0,4),对△OAB连续作旋转变换,依次得到△1、△2、△3、△4…,则△2013的直角顶点的坐标为.12.如图,ABCD是对角线互相垂直的四边形,且OB=OD,请你添加一个适当的条件____________,使ABCD成为菱形.(只需添加一个即可)13.如图,将菱形纸片ABCD折叠,使点A恰好落在菱形的对称中心O处,折痕为EF.若菱形ABCD的边长为2cm,∠A=120°,则EF=.14.如图,矩形ABCD中,AB=3,BC=4,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为_________.13题图12题图11题图ECDBAB′三、解答题(每小题5分,共20分) 15.计算:14题图16.如图8,四边形ABCD是菱形,对角线AC与BD相交于O,AB=5,AO=4,求BD的长.16题图17.先化简,后计算:,其中,.18.如图,在平行四边形ABCD中,对角线AC,BD交于点O,经过点O的直线交AB于E,交CD于F.求证:OE=OF.18题图四、解答题(每小题7分,共28分)19.在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,折痕DF交BC于点F.(1)求证:四边形BFDE为平行四边形;(2)若四边形BFDE为菱形,且AB=2,求BC的长. 19题图ABCDNMP20.如图,在四边形ABCD中,AB=BC,对角线BD平分ÐABC,P是BD上一点,过点P作PM^AD,PN^CD,垂足分别为M、N。(1)求证:ÐADB=ÐCDB;(2)若ÐADC=90°,求证:四边形MPND是正方形。20题图21.如图,在□ABCD中,F是AD的中点,延长BC到点E,使CE=BC,连结DE,CF。(1)求证:四边形CEDF是平行四边形;(2)若AB=4,AD=6,∠B=60°,求DE的长。21题图22.如图,四边形ABCD是平行四边形,DE平分∠ADC交AB于点E,BF平分∠ABC,交CD于点F.(1)求证:DE=BF;(2)连接EF,写出图中所有的全等三角形.(不要求证明)22题图五、解答题(每小题8分,共16分)23.如图,在△ABC中,∠ACB=90°,∠B>∠A,点D为边AB的中点,DE∥BC交AC于点E,CF∥AB交DE的延长线于点F.(1)求证:DE=EF;(2)连结CD,过点D作DC的垂线交CF的延长线于点G,求证:∠B=∠A+∠DGC. 23题图24.2013如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF、BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC。(1)求证;OE=OF;(2)若BC=,求AB的长。24题图六解答题:(每小题10分,共20分)25.如图1,在△OAB中,∠OAB=90°,∠AOB=30°,OB=8.以OB为边,在△OAB外作等边△OBC,D是OB的中点,连接AD并延长交OC于E.(1)求证:四边形ABCE是平行四边形;(2)如图2,将图1中的四边形ABCO折叠,使点C与点A重合,折痕为FG,求OG的长.25题图 26.如图,在等边三角形ABC中,BC=6cm.射线AG//BC,点E从点A出发沿射线AG以1cm/s的速度运动,同时点F从点B出发沿射线BC以2cm/s的速度运动,设运动时间为t(s).(1)连接EF,当EF经过AC边的中点D时,求证:△ADE≌△CDF;(2)填空:①当t为_________s时,四边形ACFE是菱形;②当t为_________s时,以A、F、C、E为顶点的四边形是直角梯形.26题图参考答案1.B;2.C;3.D;4.D;5.C;6.C;7.-7;8.≤;9.;10.25°;11.(8052,0);12.OA=OC或AD=BC或AD∥BC或AB=BC;13.;14.或3;15.;16.解:∵四边形ABCD是菱形,对角线AC与BD相交于O,∴AC⊥BD,DO=BO,∵AB=5,AO=4,∴BO==3,∴BD=2BO=2×3=6.17.:原式 当,时,原式的值为。18.证明:∵四边形ABCD是平行四边形,∴OA=OC,AB∥CD∴∠OAE=∠OCF∵∠AOE=∠COF∴△OAE≌△OCF(ASA)∴OE=OF19.(1)证明:∵四边形ABCD是矩形,∴∠A=∠C=90°,AB=CD,AB∥CD,∴∠ABD=∠CDB,∵在矩形ABCD中,将点A翻折到对角线BD上的点M处,折痕BE交AD于点E.将点C翻折到对角线BD上的点N处,∴∠ABE=∠EBD=∠ABD,∠CDF=∠CDB,∴∠ABE=∠CDF,在△ABE和△CDF中∴△ABE≌△CDF(ASA),∴AE=CF,∵四边形ABCD是矩形,∴AD=BC,AD∥BC,∴DE=BF,DE∥BF,∴四边形BFDE为平行四边形;(2)解:∵四边形BFDE为为菱形,∴BE=ED,∠EBD=∠FBD=∠ABE,∵四边形ABCD是矩形,∴AD=BC,∠ABC=90°,∴∠ABE=30°,∵∠A=90°,AB=2,∴AE==,BE=2AE=,∴BC=AD=AE+ED=AE+BE=+=2.20.(1)∵BD平分ÐABC,∴ÐABD=ÐCBD。又∵BA=BC,BD=BD,∴△ABD@△CBD。∴ÐADB=ÐCDB。(4分)(2)∵PM^AD,PN^CD,∴ÐPMD=ÐPND=90°。又∵ÐADC=90°,∴四边形MPND是矩形。∵ÐADB=ÐCDB,PM^AD,PN^CD,∴PM=PN。∴四边形MPND是正方形。 21.(1)略(2)22.证明:(1)∵四边形ABCD是平行四边形,∴DC∥AB,∴∠CDE=∠AED,∵DE平分∠ADC,∴∠ADE=∠CDE,∴∠ADE=∠AED,∴AE=AD,同理CF=CB,又AD=CB,AB=CD,∴AE=CF,∴DF=BE,∴四边形DEBF是平行四边形,∴DE=BF,(2)△ADE≌△CBF,△DFE≌△BEF.23.解答:证明:(1)∵DE∥BC,CF∥AB,∴四边形DBCF为平行四边形,∴DF=BC,∵D为边AB的中点,DE∥BC,∴DE=BC,∴EF=DF﹣DE=BC﹣CB=CB,∴DE=EF;(2)∵四边形DBCF为平行四边形,∴DB∥CF,∴∠ADG=∠G,∵∠ACB=90°,D为边AB的中点,∴CD=DB=AD,∴∠B=∠DCB,∠A=∠DCA,∵DG⊥DC,∴∠DCA+∠1=90°,∵∠DCB+∠DCA=90°,∴∠1=∠DCB=∠B,∵∠A+∠ADG=∠1,∴∠A+∠G=∠B. 24.(1)证明:∵四边形ABCD是矩形∴AB∥CD,∠OAE=∠OCF,∠OEA=∠OFC∵AE=CF∴△AEO≌△CFO(ASA)∴OE=OF(2)连接BO∵OE=OF,BE=BF∴BO⊥EF且∠EBO=∠FBO∴∠BOF=900∵四边形ABCD是矩形∴∠BCF=900又∵∠BEF=2∠BAC,∠BEF=∠BAC+∠EOA∴∠BAC=∠EOA∴AE=OE∵AE=CF,OE=OF∴OF=CF又∵BF=BF∴△BOF≌△BCF(HL)∴∠OBF=∠CBF∴∠CBF=∠FBO=∠OBE∵∠ABC=900∴∠OBE=300∴∠BEO=600∴∠BAC=300∴AC=2BC=,∴AB=25.(1)证明:∵Rt△OAB中,D为OB的中点,∴DO=DA,∴∠DAO=∠DOA=30°,∠EOA=90°,∴∠AEO=60°,又∵△OBC为等边三角形,∴∠BCO=∠AEO=60°,∴BC∥AE,∵∠BAO=∠COA=90°,∴CO∥AB,∴四边形ABCE是平行四边形;(2)解:设OG=x,由折叠可得:AG=GC=8﹣x,在Rt△ABO中,∵∠OAB=90°,∠AOB=30°,BO=8,AO=,在Rt△OAG中,OG2+OA2=AG2,x2+(4)2=(8﹣x)2,解得:x=1,∴OG=1. 26.(1)证明:∵∴∵是边的中点∴又∵∴△ADE≌△CDF(2)①∵当四边形是菱形时,∴由题意可知:,∴②若四边形是直角梯形,此时过作于M,,可以得到,即,∴,此时,重合,不符合题意,舍去。若四边形若四边形是直角梯形,此时,∵△ABC是等边三角形,F是BC中点,∴,得到经检验,符合题意。∴①②人教版八年级(下册)数学期末试题及答案 一、选择题:本大题共16个小题,1-6小题每小题2分,7-15小题每小题3分,共39分。在每小题给出的四个选项中,只有一项是符合题目要求,把这个正确的选项的序号写在括号内1.使二次根式有意义的x的取值范围是( ) A.x=1B.x≠1C.x>1D.x≥12.如图,三个正方形围成一个直角三角形,81、400分别为所在正方形的面积,则图中字母A所代表的正方形面积是( ) A.11B.31 C.319D.以上答案都不对3.如图,▱ABCD中,∠C=120°,BE平分∠ABC,则∠ABE等于( ) A.30°B.60° C.120°D.以上答案都不对4.下列各图给出了变量x与y之间的对应关系,其中y是x的函数的是( )A.B.C.D.5.某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验,得到两个品种每公顷产量的两组数据,其方差分别为s甲2=0.002、s乙2=0.03,则( ) A.甲比乙的产量稳定 B.乙比甲的产量稳定 C.甲、乙的产量一样稳定 D.无法确定哪一品种的产量更稳定6.下列二次根式中,最简二次根式是( ) A.B.C.D.7.在“大家跳起来”的乡村学校舞蹈比赛中,某校10名学生参赛成绩统计如图所示.对于这10名学生的参赛成绩,下列说法中错误的是( ) A.众数是90B.中位数是90C.平均数是90D.极差是158.一次函数y=5x+2的图象不经过的象限是( ) A.第一象限B.第二象限C.第三象限D.第四象限9.依次连接四边形ABCD各边的中点所得四边形是矩形,则四边形ABCD一定是( ) A.菱形B.对角线相等的四边形 C.矩形D.对角线互相垂直的四边形10.某班同学在探究弹簧的长度跟外力的变化关系时,实验记录得到的相应数据如下表,则y关于x的函数图象是( )砝码的质量(x克)050100150200250300400500指针位置(y厘米)2345677.57.57.5 A.B.C.D.11.一次函数y1=kx+b与y2=x+a的图象如图,则下列结论:①k<0;②a>0:③b>0;④x<2时,kx+b<x+a中,正确的个数是( ) A.1B.2C.3D.412.如图,在矩形ABCD中,AB=12cm,BC=6cm,点E、F分别在AB、CD上,将矩形ABCD沿EF折叠,使点A、D分别落在矩形ABCD外部的点A1、D1处,则整个阴影部分图形的周长为( ) A.72cmB.18cmC.40cmD.36cm13.甲、乙两人沿相同的路线由A到B匀速行进,A、B两地间的路程为16km,他们行进的路程s(km)与甲出发后的时间t(h)之间的函数图象如图所示,则下列判断错误的是( ) A乙比甲晚出发1hB.甲比乙晚到B地2h C.甲的速度是4km/hD.乙的速度是8km/h14.一个正方形和两个等边三角形的位置如图所示,若∠3=50°,则∠1+∠2=( ) A90°B.100°C.130°D.180° 15.如图,E、F分别是正方形ABCD的边CD、AD上的点,且CE=DF,AE、BF相交于点O,下列结论:(1)AE=BF;(2)AE⊥BF;(3)AO=OE;(4)S△AOB=S四边形DEOF中正确的有( ) A.4个B.3个C.2个D.1个二、填空题:本大题共4小题,每小题3分,共12分。把最简答案填在题中的横线上。16.对于任意不相等的两个实数a、b,定义运算※如下:a※b=,那么8※12= .17.若点A(1,y1)和点B(2,y2)都在一次函数y=﹣x+2的图象上,则y1 y2(选择“>”、“<”、=”填空).18.如图,矩形ABCD中,点E、F分别是AB、CD的中点,连接DE和BF,分别取DE、BF的中点M、N,连接AM,CN,MN,若AB=2,BC=2,则图中阴影部分的面积 为19.如图,已知直线l:y=x,过点M(2,0)作x轴的垂线交直线l于点N,过点N作直线l的垂线交x轴于点M1;过点M1作x轴的垂线交直线l于N1,过点N1作直线l的垂线交x轴于点M2,…;按此作法继续下去,则点M10的坐标为 .三、解答题:本大题共6小题,共69分,解答应写出文字说明、说理过程或演算步骤。20.计算(18分)(1)(4﹣3)(2)(3)甲、乙两台机床同时生产一种零件,在10天中,两台机床每天出次品的数量如表:甲0102203124乙2311021101请计算两组数据的方差. 21.在某小区的A处有一个凉亭,道路AB、BC、AC两两相交于点A、B、C,并且道路AB与道路BC互相垂直,如图所示.已知A与B之间的距离为20cm,若有两个小朋友在与点B相距10cm的点D处玩耍,玩累了他们分别沿不同的路线D→B→A,D→C→A到凉亭A处喝水休息,已知路线D→B→A与D→C→A路程相等,求AC的长度.(8分)22.如图,A(0,1),M(3,2),N(4,4).动点P从点A出发,沿y轴以每秒1个单位长的速度向上移动,且过点P的直线l:y=﹣x+b也随之移动,设移动时间为t秒.(1)当t=3时,求直线的解析式;(2)当直线通过点M时,求直线l的解析式;(3)若点M,N位于l的异侧,确定t的取值范围.(12分) 23.某高中学校为使高一新生入校后及时穿上合身的校服,现提前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查,并根据调查结果绘制了如图两个不完整的统计图(校服型号以身高作为标准,共分为6种型号)(11分)根据以上信息,解答下列问题:(1)该班共有 名学生,其中穿175型校服的学生有 名.(2)在条形统计图中,请把空缺部分补充完整.(3)该班学生所穿校服型号的众数为 ,中位数为 .24.某单位准备印刷一批书面材料,现有两个印刷厂可供选择,甲厂的费用分为制作费和印刷费两部分,乙厂直接按印刷数量收取印刷费.甲厂的费用y(千元)与书面材料数量x(千份)的关系见表:书面材料数量x(千份)0123456…甲厂的印刷费用y(千元)11.522.533.54…乙厂的印刷费用y(千元)与书面材料数量x(千份)的函数关系图象如图所示.(1)请你写出甲厂的费用y与x的函数解析式,并在图中坐标系中画出甲厂的费用y与x的函数图象.(2)请写出乙厂费用y与x的函数解析式,试求出当x在什么范围内时乙厂比甲厂的费用低?(3)现有一客户需要印10千份书面材料,请问你如果是客户你如何选择?(8分) 25.实践与操作:(14分)(1)①利用尺规按下列要求作图,并在图中标明相应的字母(保留作图痕迹,不写作法):作线段AC的垂直平分线MN,垂足为O;②连接BO,并延长BO到点D,26.(2014•路南区一模)如图,已知,在Rt△ABC中,∠BAC=90°.使得OD=BO,连接AD、CD;③分别在OA、OC的延长线上取点E、F,使AE=CF,连接BF、FD、DE、EB.推理与运用:(2)①求证:四边形BFDE是平行四边形;②若AB=4,AC=6,求当AE的长为多少时,四边形BFDE是矩形. 数学试卷答案一、选择题:本大题共16个小题,1-6小题每小题2分,7-15小题每小题分,共39分。1.解答:解:∵二次根式有意义,∴可得x﹣1≥0,解得x≥1.故选D. 2.解答:解:如图所示:根据题意得:∠BCD=90°,BD2=400,CD2=81,∴BC2=BD2﹣CD2=319,∴图中字母A所代表的正方形面积=BC2=319;故选:C. 3.解答:解:∵∠C=120°,∴∠ABC=60°,又∵BE平分∠ABC,∴∠ABE=30°.故选A. 4.解答:解:∵对于x的每一个取值,y都有唯一确定的值,A、对于x的每一个取值,y都有两个值,故A错误;B、对于x的每一个取值,y都有两个值,故B错误;C、对于x的每一个取值,y都有两个值,故C错误;D、对于x的每一个取值,y都有唯一确定的值,故D正确;故选:D..5,解答:解:∵s甲2=0.002、s乙2=0.03,∴s甲2<s乙2,∴甲比乙的产量稳定.故选A6.解答:解:A、=,被开方数含分母,不是最简二次根式;故A选项错误;B、=,被开方数为小数,不是最简二次根式;故B选项错误;C、,是最简二次根式;故C选项正确;D.=5,被开方数,含能开得尽方的因数或因式,故D选项错误;故选C. 7.解答:解:∵90出现了5次,出现的次数最多,∴众数是90;故A正确;∵共有10个数,∴中位数是第5、6个数的平均数,∴中位数是(90+90)÷2=90;故B正确;∵平均数是(80×1+85×2+90×5+95×2)÷10=89;故C错误;极差是:95﹣80=15;故D正确.综上所述,C选项符合题意, 故选:C. 8.解答:解:∵k=5>0,图象过一三象限,b=2>0,图象过第二象限,∴直线y=5x+2经过一、二、三象限,不经过第四象限.故选D.9.解答:解:如图,连接AC、BD,∵E、F、G、H分别是AB、BC、CD、DA的中点,∴EH∥BD,EF∥AC,∴∠1=∠2,∠2=∠3,∴∠1=∠3,∵四边形EFGH是矩形,∴∠1=90°,∴∠3=90°,∴AC⊥BD,即原四边形ABCD的对角线互相垂直,故选D. 10.解答:解:根据图表可以知道,在没有砝码时指针的位置是2cm,以后砝码每增加50g,指针位置增加1cm,则当是275g时,弹簧指针位置应是7.5cm,以后,指针位置不随砝码的增加而伸长,都是7.5cm.故选C.11.解答:解:∵直线=kx+b过第一、二、四象限,∴k<0,b>0,所以①③正确;∵直线y2=x+a的图象与y轴的交点在x轴下方,∴a<0,所以②错误;当x>3时,kx+b<x+a,所以④错误.故选B.12..解答:解:根据折叠的性质,得A1E=AE,A1D1=AD,D1F=DF.则阴影部分的周长=矩形的周长=2(12+6)=36(cm).故选:D.13.解答:解:分析题意和图象可知:乙比甲晚出发1h;甲比乙晚到B地4﹣2=2h;甲的速度是16÷4=4km/h;乙的速度是16÷1=16km/h. 故选D14.解答:解:如图,∠BAC=180°﹣90°﹣∠1=90°﹣∠1,∠ABC=180°﹣60°﹣∠3=120°﹣∠3,∠ACB=180°﹣60°﹣∠2=120°﹣∠2,在△ABC中,∠BAC+∠ABC+∠ACB=180°,∴90°﹣∠1+120°﹣∠3+120°﹣∠2=180°,∴∠1+∠2=150°﹣∠3,∵∠3=50°,∴∠1+∠2=150°﹣50°=100°.故选:B.. 15.解答:解:∵四边形ABCD为正方形,∴AB=AD=DC,∠BAD=∠D=90°,而CE=DF,∴AF=DE,在△ABF和△DAE中,∴△ABF≌△DAE,∴AE=BF,所以(1)正确;∴∠ABF=∠EAD,而∠EAD+∠EAB=90°,∴∠ABF+∠EAB=90°,∴∠AOB=90°,∴AE⊥BF,所以(2)正确;连结BE,∵BE>BC,∴BA≠BE,而BO⊥AE,∴OA≠OE,所以(3)错误;∵△ABF≌△DAE,∴S△ABF=S△DAE,∴S△ABF﹣S△AOF=S△DAE﹣S△AOF,∴S△AOB=S四边形DEOF,所以(4)正确.故选:B. 二、填空题:16.解答:解:8※12===﹣,故答案为:﹣.17.解答:解:∵k=﹣1<0,∴函数值y随x的增大而减小,∵1<2,∴y1>y2.故答案为:>.18.19.解答:解:∵点E、F分别是AB、CD的中点,M、N分别为DE、BF的中点,∴矩形绕中心旋转180°阴影部分恰好能够与空白部分重合,∴阴影部分的面积等于空白部分的面积,∴阴影部分的面积=×矩形的面积,∵AB=2,BC=2,∴阴影部分的面积=×2×2=2.故答案为:2. 19.解答:解:∵直线l的解析式是y=x,∴∠NOM=60°,∠ONM=30°.∵点M的坐标是(2,0),NM∥y轴,点N在直线y=x上, ∴NM=2,∴ON=2OM=4.又∵NM1⊥l,即∠ONM1=90°∴OM1=2ON=41OM=8.同理,OM2=4OM1=42OM,OM3=4OM2=4×42OM=43OM,…OM10=410OM=2097152.∴点M10的坐标是(2097152,0).故答案是:(2097152,0).三、解答题:本大题共6小题,共66分,解答应写出文字说明、说理过程或演算步骤。20.解答:解:(1)原式=4﹣3+2=2﹣3;(2)原式=﹣3﹣2+﹣3=0;(3)甲的平均数=(0+1+0+2+2+0+3+1+2+4)=1.5,乙的平均数=(2+3+1+1+0+2+1+1+0+1)=1.2,甲的方差=×[3×(0﹣1.5)2+2×(1﹣1.5)2+3×(2﹣1.5)2+(3﹣1.5)2+(4﹣1.5)2]=16.5;乙的方差=×[2×(0﹣1.5)2+5×(1﹣1.5)2+2×(2﹣1.5)2+(3﹣1.5)2]=8.5.21.解答:解:如图:设AC的距离为xm,则DC的长为(30﹣x)m,则BC的长为(40﹣x)m,在Rt△ABC中,由勾股定理得:AB2+BC2=AC2,即:202+(40﹣x)2=x2解得:x=25m答:AC之间的距离是25m. 22.解答:解:(1)当t=3时,P坐标为(0,4),把P坐标代入直线l解析式得:b=4,则此时直线解析式为y=﹣x+4;(2)把M(3,2)代入直线l解析式得:2=﹣3+b,即b=5,此时直线l解析式为y=﹣x+5;(3)把N(4,4)代入直线l解析式得:4=﹣4+b,即b=8,此时直线l解析式为y=﹣x+8,当直线l过M点时,令y=﹣x+5中x=0,得到y=5,即P(0,5),此时t=4;当直线l过N点时,令y=﹣x+8中x=0,得到y=8,即P(0,8),此时t=7,则点M,N位于l的异侧,t的取值范围为4<t<7.23.(根据以上信息,解答下列问题:(1)该班共有 50 名学生,其中穿175型校服的学生有 10 名.(2)在条形统计图中,请把空缺部分补充完整.(3)该班学生所穿校服型号的众数为 165,170 ,中位数为 170解答:解:(1)15÷30%=50(名),50×20%=10(名),答:该班共有50名学生,其中穿175型校服的学生有10名;故答案为:50,10.(2)185型的学生人数为:50﹣3﹣15﹣15﹣10﹣5=50﹣48=2(名),补全统计图如图所示;(3)该班学生所穿校服型号的众数为165,170,中位数为170.故答案为:165,170,170.24,解答:解:(1)设y甲=mx+n,将(0,1),(1,1.5)代入,甲厂的费用为:y甲=x+1,书面材料印刷单价为0.5元,图象如图所示: (2)当0≤x≤2时,设乙厂的费用y(千元)与书面材料数量x(千份)的函数解析式为y乙=kx,由已知得2k=3,解得k=1.5,所以y乙=1.5x(0≤x≤2);当x>2时,由图象可设y乙与x的函数解析式为y乙=k′x+b,由已知得,解得,所以y乙=x+(x>2);解方程组,得.解方程组,解得.所以两函数的交点坐标为(1,1.5),(6,4),观察图象,可得当0<x<1或x>6时,乙厂比甲厂的印刷费用低;(3)当x=10时,甲厂的印刷费用:y甲=×10+1=6,乙厂的印刷费用:y乙=×10+=5,甲厂比乙厂多花:6﹣5=1千元.故该客户应选择乙厂. 25解答:(1)解:如图所示 (2)①证明:∵MN是AC的垂直平分线,∴OA=OC,∵AE=CF,∴OA+AE=OC+CF,即OE=OF,∵OD=BO,∴四边形BFDE是平行四边形②解:在Rt△ABC中,∠BAC=90°,AB=4,AC=6,∴OA=OC=3,∴OB==5,∵OD=BO=5,∴当四边形BFDE是矩形时,∠BED=90°,∴EO=BD=5,∴AE=EO﹣OA=2.八年级期末数学模拟考试试题一、选择题(每小题3分,共30分)1、在函数y=中,自变量x的取值范围是()A.B.C.D.2、下列计算正确的是()A.B. C. D.3、下列说法中错误的是( )A.两条对角线互相平分的四边形是平行四边形;B.两条对角线相等的四边形是矩形;C.两条对角线互相垂直的矩形是正方形;D.两条对角线相等的菱形是正方形4、刘翔为了迎战2008年北京奥运会刻苦进行110米拦训练,教练对他的10次训练成绩进行统计分析,若要判断他的成绩是否稳定,则教练需要知道刘翔这10次成绩的()A.平均数B.中位数C.众数D.方差 5、点P(3,2)关于轴的对称点的坐标是()A.(3,-2)B.(-3,2)C.(-3,-2)D.(3,2)6、下列运算中正确的是()A.B.C.D.7、如图,已知P、Q是△ABC的BC边上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小为()A.120°B.110°C.100°D.90°8、如图,在□ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )A.6 B.4 C.3 D.2EFDCBA9、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了骑车的速度继续匀速行驶,下面是行使路程(米)关于时间(分)的函数图象,那么符合这个同学行驶情况的图像大致是()A.B.C.D.10、如图是用若干个全等的等腰梯形拼成的图形,下列说法错误的是( )A.梯形的下底是上底的两倍B.梯形最大角是120°C.梯形的腰与上底相等D.梯形的底角是60°二、填空题(每小题3分,共30分)11、若分式的值为零,则x的值是.12、已知1纳米=米,一个纳米粒子的直径是35纳米,这一直径可用科学计数法表示为米.13、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E ,那么图中全等的三角形共有对.C14、如图,,要使,则需要补充一个条件,这个条件可以是.15、已知y与x-3成正比例,当x=4时,y=-1;那么当x=-4时,y=。16、已知样本x,99,100,101,y的平均数为100,方差是2,则x=,y=.17、将直线y=3x向下平移2个单位,得到直线.18、如图,在中,,,是线段的垂直平分线,交于,交于,则________。19、已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是。20、甲、乙两个工程队共同完成一项工程,乙队先单独做1天,再由两队合作2天就完成全部工程,已知甲队与乙队的工作效率之比是3:2,求甲、乙两队单独完成此项工程各需多少天?若设甲队单独完成此项工程需x天,由题意可列方程为____________。三、解答题(共60分)21、(本题8分)化简并求值:(+)÷,其中x=0。22、(本题10分)已知:锐角△ABC,求作:点P,使PA=PB,且点P到边AB的距离和到边AC的距离相等。(不写作法,保留作图痕迹)23、(本题10分)如图,在□中,分别是边和上的点.请你补充一个条件,使,并给予证明. 24、(本题10分)某老师计算学生的学期总评成绩时按照如下的标准:平时成绩占20%,期中成绩占30%,期末成绩占50%.小东和小华的成绩如下表所示:学生平时成绩期中成绩期末成绩小东708090小华907080请你通过计算回答:小东和小华的学期总评成绩谁较高?25、(本题12分)某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。(1)根据图象,求一次函数的解析式;(2)当销售单价x在什么范围内取值时,销售量y不低于80件。xy140012010012014080160 26、(本题12分)如图,、分别是矩形的对角线、上两点,且.求证:(1)≌;(2)四边形是等腰梯形.参考答案一、选择题(每小题3分,共30分)1.A2.B3.B4.D5.A6.C7.A8.D9.C10.D二、填空题(每小题3分,共30分)11、12、13、414、答案不唯一。15、716、98,10217、18、24°19、26cm20、三、解答题(共60分)21、(本题8分)化简并求值。解:(3分) (5分) (6分)当时,原式=.(8分)22、(本题8分)图略,要求保留作图痕迹。23、(本题10分)解:若EC=FA(2分)∵是平行四边形,∴AB=CD,∠B=∠D,BC=DA,(5分)又∵EC=FA,∴BE=DF,(8分)∴(10分)24、(本题10分)解:小东:70×20%+80×30%+90×50%(2分) =14+24+45=83(4分)小华:90×20%+70×30%+80×50%(6分) =18+21+40=79(8分)答:所以,小东的成绩较好。(10分)25、(本题12分)解:(1)设一次函数的解析式为,由已知条件,得(2分)(5分)解之得(7分)所以,。(8分)(2)若≥80,即≥80,解之得≥160.(12分)26、(本题12分)证明:(1)矩形的对角线、相交于,,,.又,.(3分)在和中;,,,≌;(6分)(2)在等腰中,, 在等腰中,,,又,,(9分)由(1)≌,,四边形是等腰梯形。(12分)八年级期末数学模拟考试试题一、选择题(每小题3分,共30分)1、在函数y=中,自变量x的取值范围是()A.B.C.D.2、下列计算正确的是()A.B. C. D.3、下列说法中错误的是( )A.两条对角线互相平分的四边形是平行四边形;B.两条对角线相等的四边形是矩形;C.两条对角线互相垂直的矩形是正方形;D.两条对角线相等的菱形是正方形4、刘翔为了迎战2008年北京奥运会刻苦进行110米拦训练,教练对他的10次训练成绩进行统计分析,若要判断他的成绩是否稳定,则教练需要知道刘翔这10次成绩的()A.平均数B.中位数C.众数D.方差5、点P(3,2)关于轴的对称点的坐标是()A.(3,-2)B.(-3,2)C.(-3,-2)D.(3,2)6、下列运算中正确的是()A.B.C.D.7、如图,已知P、Q是△ABC的BC边上的两点,且BP=PQ=QC=AP=AQ,则∠BAC的大小为()A.120°B.110°C.100°D.90° 8、如图,在□ABCD的面积是12,点E,F在AC上,且AE=EF=FC,则△BEF的面积为( )A.6 B.4 C.3 D.2EFDCBA9、小明骑自行车上学,开始以正常速度匀速行驶,但行至中途自行车出了故障,只好停下来修车,车修好后,因怕耽误上课,他比修车前加快了骑车的速度继续匀速行驶,下面是行使路程(米)关于时间(分)的函数图象,那么符合这个同学行驶情况的图像大致是()A.B.C.D.10、如图是用若干个全等的等腰梯形拼成的图形,下列说法错误的是( )A.梯形的下底是上底的两倍B.梯形最大角是120°C.梯形的腰与上底相等D.梯形的底角是60°二、填空题(每小题3分,共30分)11、若分式的值为零,则x的值是.12、已知1纳米=米,一个纳米粒子的直径是35纳米,这一直径可用科学计数法表示为米.13、如图,已知OA=OB,点C在OA上,点D在OB上,OC=OD,AD与BC相交于点E,那么图中全等的三角形共有对.C14、如图,,要使,则需要补充一个条件,这个条件可以是.15、已知y与x-3成正比例,当x=4时,y=-1;那么当x=-4时,y=。16、已知样本x,99,100,101,y的平均数为100,方差是2, 则x=,y=.17、将直线y=3x向下平移2个单位,得到直线.18、如图,在中,,,是线段的垂直平分线,交于,交于,则________。19、已知三角形的3条中位线分别为3cm、4cm、6cm,则这个三角形的周长是。20、甲、乙两个工程队共同完成一项工程,乙队先单独做1天,再由两队合作2天就完成全部工程,已知甲队与乙队的工作效率之比是3:2,求甲、乙两队单独完成此项工程各需多少天?若设甲队单独完成此项工程需x天,由题意可列方程为____________。三、解答题(共60分)21、(本题8分)化简并求值:(+)÷,其中x=0。22、(本题10分)已知:锐角△ABC,求作:点P,使PA=PB,且点P到边AB的距离和到边AC的距离相等。(不写作法,保留作图痕迹)23、(本题10分)如图,在□中,分别是边和上的点.请你补充一个条件,使,并给予证明.24、(本题10分)某老师计算学生的学期总评成绩时按照如下的标准:平时成绩占20%,期中成绩占30%,期末成绩占50%.小东和小华的成绩如下表所示:学生平时成绩期中成绩期末成绩小东708090小华907080请你通过计算回答:小东和小华的学期总评成绩谁较高? 25、(本题12分)某商店试销一种成本单价为100元/件的运动服,规定试销时的销售单价不低于成本单价,又不高于180元/件,经市场调查,发现销售量y(件)与销售单价x(元)之间的关系满足一次函数y=kx+b(k≠0),其图象如图。(1)根据图象,求一次函数的解析式;(2)当销售单价x在什么范围内取值时,销售量y不低于80件。xy14001201001201408016026、(本题12分)如图,、分别是矩形的对角线、上两点,且.求证:(1)≌;(2)四边形是等腰梯形. 参考答案一、选择题(每小题3分,共30分)1.A2.B3.B4.D5.A6.C7.A8.D9.C10.D二、填空题(每小题3分,共30分)11、12、13、414、答案不唯一。15、716、98,10217、18、24°19、26cm20、三、解答题(共60分)21、(本题8分)化简并求值。解:(3分) (5分) (6分)当时,原式=.(8分)22、(本题8分)图略,要求保留作图痕迹。23、(本题10分)解:若EC=FA(2分)∵是平行四边形,∴AB=CD,∠B=∠D,BC=DA,(5分)又∵EC=FA,∴BE=DF,(8分)∴(10分)24、(本题10分)解:小东:70×20%+80×30%+90×50%(2分) =14+24+45=83(4分)小华:90×20%+70×30%+80×50%(6分) =18+21+40=79(8分)答:所以,小东的成绩较好。(10分)25、(本题12分)解:(1)设一次函数的解析式为,由已知条件,得(2分)(5分)解之得(7分)所以,。(8分)(2)若≥80,即≥80,解之得≥160.(12分)26、(本题12分)证明:(1)矩形的对角线、相交于,,,.又,.(3分)在和中;,,,≌;(6分)(2)在等腰中,,在等腰中,,,又,,(9分)由(1)≌,,四边形是等腰梯形。(12分)八年级数学下册期末试题一、选择题:本大题共8个小题,每小题3分,共24分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.下列各式中,是分式的是A. B. C. D.2.分式的值为0,则A. B. C. D.3.甲、乙两人进行射击测试,每人10次射击成绩的平均数均是9.2环,方差分别为:S甲2=0.58,S乙2=0.52,则成绩最稳定的是A.甲B.乙C.甲和乙一样D.无法判定4.一次函数的图象大致是A.B.C.D.5.如图所示,四边形的对角线和相交于点,下列判断正确的是 A.若,则是平行四边形 B.若,则是平行四边形 C.若,,则是平行四边形D.若,,则是平行四边形. 6.如图,菱形的顶点的坐标为(6,8).顶点在轴的正半轴上,反比例函数的图象经过顶点,则的值为A.128B.120C.48D.1407.矩形中,,,⊥于点,则的长为A.4B.3C.2.5D.2.4ABCDO(第5题图)(第6题图)8.关于函数有如下结论:①函数图象一定经过点(-2,-3)②函数图象在第一、三象限③函数值随的增大而减小④当时,函数的取值范围为,这其中正确的有A.1个B.2个C.3个D.4个二、填空题:本大题共8个小题,每小题3分,共24分.请把答案直接填在答题卡对应题中横线上.9.某种呼吸综合症病毒的直径为0.000000012米,将这个数用科学记数法表示为米. 10.函数中,自变量的取值范围是.11.计算:=.12.直线向上平移4个单位得到的直线的解析式为:____________.13.平行四边形的周长为36,相邻两边的比为1:2,则它的较短边长是_________.14.一组数据1,2,的平均数为2,另一组数据-l,,1,2,的唯一众数为-l,则数据-1,,1,2,的中位数为.ADCEFBMN(第16题图)O15.若A,B,C都是反比例函数的图象上的点,且,则由小到大的顺序是.16.如图,正方形的边长为2,对角线、相交于点,把放在正方形上,使直角顶点与点重合,让绕着点旋转,、分别交、于点、.给出下列结论:①②四边形OMCN③;④的最短距离为.其中正确的结论是.(只填番号)三、解答题:本大题共8个题,共72分.解答应写出文字说明,证明过程或演算步骤.17.(每小题5分,共15分)(1)计算:++(2)解方程(3)先化简,再求代数式的值:,其中是之间的整数,请选一个合适的求解.ABCDEF18.(本小题6分)如图,四边形是平行四边形,、在对角线上,且,求证:四边形是平行四边形.19.(本小题9分)442861210181614人数捐款(元)5101520257149图1AB28%DECA:5元B:10元C:15元D:20元E:25元图2某校一学生身患白血病,该校八年级(1)班全体同学参加了学校组织的捐款活动,捐款情况的部分统计图如图所示:(1)求该班的总人数;(2)将条形图补充完整;(3)该班平均每人捐款多少元? 20.(本小题6分)某市为治理污水,需要铺设一段全长为3000的污水排放管道.为了尽量减少施工对城市交通所造成的影响,实际施工时每天的工效比原计划增加25%,结果提前30天完成这一任务.实际每天铺设多长管道?y(千米)x(小时)21.(本小题8分)一辆慢车与一辆快车分别从甲、乙两地同时出发,匀速相向而行,两车在途中相遇后都停留一段时间,然后分别按原速一同驶往甲地后停车.设慢车行驶的时间为小时,两车之间的距离为千米,图中折线表示与之间的函数图象,请根据图象解决下列问题:(1)甲乙两地之间的距离为 千米;(2)求快车和慢车的速度;(3)求线段DE所表示的与之间的函数关系式,并写出自变量的取值范围.22.(本小题8分)如图,已知中,是边上的中点,是的中点,过点作的平行线,交的延长线于点,连接.(1)求证:;(2)如果,试判断四边形的形状,并证明你的结论.23.(本小题10分)如图,已知正比例函数和反比例函数的图象交于点A(,)和点.(1)求反比例函数的解析式;(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量的取值范围;(3)若双曲线上点C(4,)沿方向平移5个单位长度得到点,判断四边形的形状并证明你的结论. 24.(本小题10分)BACOGFExy如图,在直角坐标系中,四边形为矩形,点在轴上,点C在轴上,点的坐标是(12,8),点是线段上的一点,点(12,5)在线段上,将矩形沿直线折叠,使点落在边上的点处.(1)求点的坐标;(2)求直线的解析式;(3)坐标系内是否存在点,使以点,,,为顶点的四边形为平行四边形?若存在,直接写出点的坐标,若不存在,请说明理由..(初二下数学期末试题(时间:120分钟)一、细心填一填,一锤定音(每小题给出的四个选项中,只有一个是正确的,请把正确的选项选出来,并将正确选项填入答题卡中)题号123456789101112答案1、同学们都知道,蜜蜂建造的蜂房既坚固又省料。那你知道蜂房蜂巢的厚度吗?事实上,蜂房的蜂巢厚度仅仅约为0.000073m。此数据用科学计数法表示为()A、B、C、D、2、若一个四边形的两条对角线相等,则称这个四边形为对角线四边形。下列图形不是对角线四边形的是()A、平行四边形B、矩形C、正方形D、等腰梯形3、某地连续10天的最高气温统计如下:最高气温(℃)22232425天数1234这组数据的中位数和众数分别是()A、24,25B、24.5,25C、25,24D、23.5,244、下列运算中,正确的是() A、B、C、D、5、下列各组数中以a,b,c为边的三角形不是Rt△的是( )A、a=2,b=3,c=4B、a=5,b=12,c=13C、a=6,b=8,c=10D、a=3,b=4,c=56、一组数据0,-1,5,x,3,-2的极差是8,那么x的值为()A、6B、7C、6或-3D、7或-37、已知点(3,-1)是双曲线上的一点,则下列各点不在该双曲线上的是()A、B、C、(-1,3)D、(3,1)8、下列说法正确的是()A、一组数据的众数、中位数和平均数不可能是同一个数B、一组数据的平均数不可能与这组数据中的任何数相等C、一组数据的中位数可能与这组数据的任何数据都不相等D、众数、中位数和平均数从不同角度描述了一组数据的波动大小9、如图(1),已知矩形的对角线的长为,连结各边中点、、、得四边形,则四边形的周长为()A、B、C、D、10、若关于x的方程无解,则m的取值为()A、-3B、-2C、-1D、311、在正方形ABCD中,对角线AC=BD=12cm,点P为AB边上的任一点,则点P到AC、BD的距离之和为()BDCA图(2)……图(1)A、6cmB、7cmC、cmD、cm12、如图(2)所示,矩形ABCD的面积为10,它的两条对角线交于点,以AB、为邻边作平行四边形,平行四边形的对角线交于点,同样以AB、为邻边作平行四边形,……,依次类推,则平行四边形的面积为()A、1B、2C、D、 二、细心填一填,相信你填得又快又准13、若反比例函数的图像在每个象限内y随x的增大而减小,则k的值可以为_______(只需写出一个符合条件的k值即可)14、某中学八年级人数相等的甲、乙两个班级参加了同一次数学测验,两班平均分和方差分别为分,分,,则成绩较为整齐的是________(填“甲班”或“乙班”)。15、如图(3)所示,在□ABCD中,E、F分别为AD、BC边上的一点,若添加一个条件_____________,则四边形EBFD为平行四边形。16、如图(4),是一组数据的折线统计图,这组数据的平均数是,极差是.17、如图(5)所示,有一直角梯形零件ABCD,AD∥BC,斜腰DC=10cm,∠D=120°,则该零件另一腰AB的长是_______cm;ABCDEF图(3)图(4)图(6)ABCD图(5)5618、如图(6),四边形是周长为的菱形,点的坐标是,则点的坐标为.图(7)19、如图(7)所示,用两块大小相同的等腰直角三角形纸片做拼图游戏,则下列图形:①平行四边形(不包括矩形、菱形、正方形);②矩形(不包括正方形);③正方形;④等边三角形;⑤等腰直角三角形,其中一定能拼成的图形有__________(只填序号)。20、任何一个正整数n都可以进行这样的分解:(s、t是正整数,且s≤t),如果在n的所有这种分解中两因数之差的绝对值最小,我们就称是最佳分解,并规定。例如:18可以分解成1×18,2×9,3×6,这是就有。结合以上信息,给出下列的说法:①;②;③;④若n是一个完全平方数,则,其中正确的说法有_________.(只填序号)三、开动脑筋,你一定能做对(解答应写出文字说明、证明过程或推演步骤) 21、解方程22、先化简,再求值,其中x=223、某校八年级(1)班50名学生参加2007年济宁市数学质量监测考试,全班学生的成绩统计如下表:成绩(分)71747880828385868890919294人数1235453784332请根据表中提供的信息解答下列问题:(1)该班学生考试成绩的众数和中位数分别是多少?(2)该班张华同学在这次考试中的成绩是83分,能不能说张华同学的成绩处于全班中偏上水平?试说明理由. 24、如图(8)所示,由5个大小完全相同的小正方形摆成如图形状,现移动其中的一个小正方形,请在图(8-1)、图(8-2)、图(8-3)中分别画出满足以下要求的图形.(用阴影表示)(1)使所得图形成为轴对称图形,而不是中心对称图形;(2)使所得图形成为中心对称图形,而不是轴对称图形;(3)使所得图形既是轴对称图形,又是中心对称图形.图(8-1)图(8-2)图(8-3)图(8)25、某青少年研究机构随机调查了某校100名学生寒假零花钱的数量(钱数取整数元),以便研究分析并引导学生树立正确的消费观.现根据调查数据制成了如下图所示的频数分布表.(1)请将频数分布表和频数分布直方图补充完整;(2)研究认为应对消费150元以上的学生提出勤俭节约合理消费的建议.试估计应对该校1200名学生中约多少名学生提出该项建议?(3)你从以下图表中还能得出那些信息?(至少写出一条)频数(人数)155203025100.550.5200.5300.5寒假消费(元)150.5100.5250.5频数分布表频数分布直方图分组(元)组中值(元)频数频率0.5~50.525.50.150.5~100.575.5200.2100.5~150.5150.5~200.5175.5300.3200.5~250.5225.5100.1250.5~300.5275.550.05合计100 26、如图(9)所示,一次函数的图像与反比例函数的图像交于M、N两点。xyO·(3,2)图(9)·NM(-1,a)(1)根据图中条件求出反比例函数和一次函数的解析式;(2)当x为何值时一次函数的值大于反比例函数的值?BEDFCA图(10)27、如图(10)所示,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm。求CE的长?28、如图(11)所示,在梯形ABCD中,AD∥BC,∠B=90°,AD=24cm,BC=26cm,动点P从点A出发沿AD方向向点D以1cm/s的速度运动,动点Q从点C开始沿着CB方向向点B以3cm/s的速度运动。点P、Q分别从点A和点C同时出发,当其中一点到达端点时,另一点随之停止运动。Q图(11))PDCBA(1)经过多长时间,四边形PQCD是平行四边形?(2)经过多长时间,四边形PQBA是矩形? (3)经过多长时间,四边形PQCD是等腰梯形?八年级数学试题答案一、选择题(3分×12=36分)题号123456789101112答案BAADACDCABAD二、填空题(3分×8=24分)13、k>4的任何值(答案不唯一); 14、___甲班___; 15、答案不唯一;16、46.5,31; 17、cm;18、(0,3);19、__①③⑤__;20、__①③④__.三、开动脑筋,你一定能做对(共60分)21、(6分)解:方程两边同乘得:4分解得:6分检验:把代入=0所以-2是原方程的增根,原方程无解.4分22、(6分)解:原式=6分把x=2代入原式=86分23、(8分)(1)众数为88,中位数为86;8分(2)不能,理由略.图(8-1)图(8-2)图(8-3)24、(6分)4分25、(9分)(1)略7分(2)(名)9分(3)略26、(8分)解:(1)反比例函数解析式为:6分一次函数的解析式为:8分(2)当或时一次函数的值大于反比例函数的值.27、(8分)CE=3 28、(9分)(1)(3分)设经过,四边形PQCD为平行四边形,即PD=CQ,所以得(2)(3分)设经过,四边形PQBA为矩形,即AP=BQ,所以得(3)(3分)设经过,四边形PQCD是等腰梯形.(过程略)八年级数学试题期末考试1一、选择题(每空2分,共14分)1、若为实数,且,则的值为( )A.1 B. C.2 D.2、有一个三角形两边长为4和5,要使三角形为直角三角形,则第三边长为( )A、3 B、 C、3或 D、3或 3、如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是( )A.7,24,25 B.,, C.3,4,5 D.4,,4、如下图,在中,分别是边的中点,已知,则的长为( )A.3 B.4 C.5 D.65、已知点(-2,y1),(-1,y2),(1,y3)都在直线y=-3x+b上,则y1,y2,y3的值的大小关系是( )A.y1>y2>y3 B.y1查看更多