八年级下数学课件《矩形的性质与判定 三 》参考课件_鲁教版

八年级下数学课件《矩形的性质与判定 三 》参考课件_鲁教版

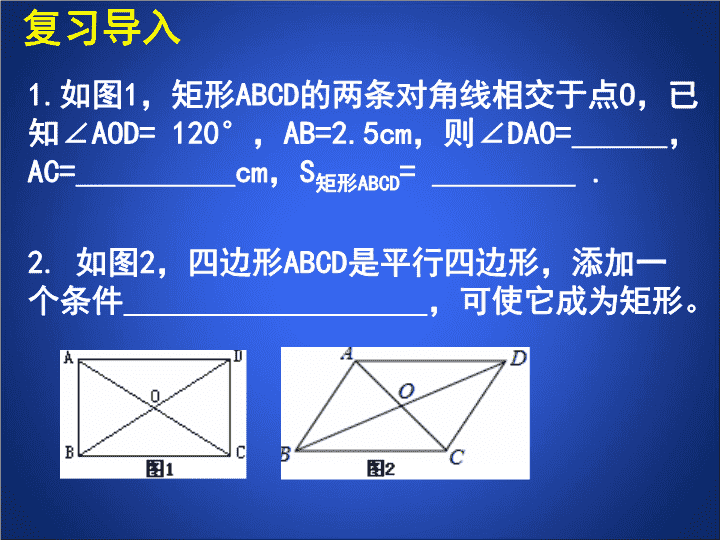
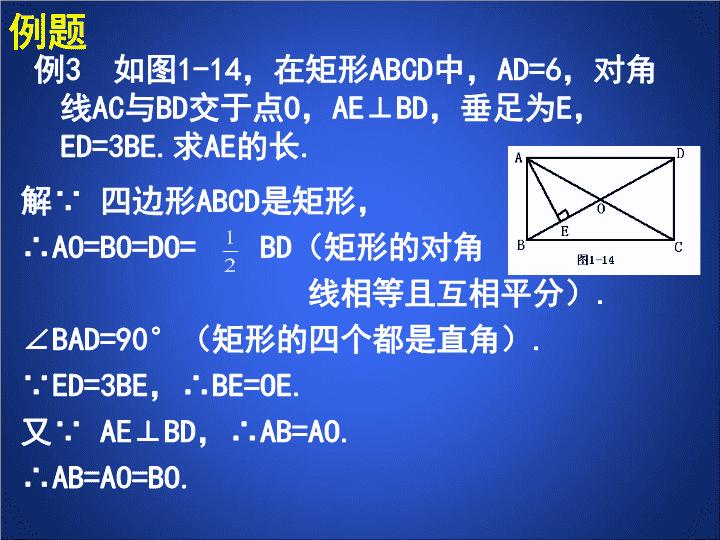
特殊平行四边形矩形的性质与判定（三） 1.如图1，矩形ABCD的两条对角线相交于点O，已知∠AOD=120°，AB=2.5cm，则∠DAO=，AC=cm，S矩形ABCD=.2.如图2，四边形ABCD是平行四边形，添加一个条件，可使它成为矩形。复习导入 例3如图1-14，在矩形ABCD中，AD=6，对角线AC与BD交于点O，AE⊥BD，垂足为E，ED=3BE.求AE的长.例题解∵四边形ABCD是矩形，∴AO=BO=DO=BD（矩形的对角线相等且互相平分）.∠BAD=90°（矩形的四个都是直角）.∵ED=3BE，∴BE=OE.又∵AE⊥BD，∴AB=AO.∴AB=AO=BO. 例3如图1-14，在矩形ABCD中，AD=6，对角线AC与BD交于点O，AE⊥BD，垂足为E，ED=3BE.求AE的长.例题你还有其他的解法吗？和同学交流即△ABO是等边三角形.∴∠ABO=60°.∴∠ADB=90°-∠ABO=30°.在Rt△AED中，∵∠ADB=30°，∴AE=AD=×6=3. 例4如图1-15，在△ABC中，AB=AC，AD为∠BAC的平分线，AN为△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.求证：四边形ADCE是矩形.例题证明：∵AD平分∠BAC，AN平分∠CAM，∴∠CAD=∠BAC，∠CAN=∠CAM.∴∠DAE=∠CAD+∠CAN=（∠BAC+∠CAM）=×180°=90°. 例4如图1-15，在△ABC中，AB=AC，AD为∠BAC的平分线，AN为△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.求证：四边形ADCE是矩形.例题在△ABC中，∵AB=AC，AD为∠BAC的平分线，∴AD⊥BC.∴∠ADC=90°.又∵CE⊥AN，∴∠CEA=90°.∴四边形ADCE为矩形（有三个角是直角的四边形是矩形）.你还有其他的解法吗？和同学交流 巩固提高在例题4中，若连接DE，交AC于点F（如图1-16）（1）试判断四边形ABDE的形状，并证明你的结论.（2）线段DF与AB有怎样的关系？请证明你的结论. 已知：如图，四边形ABCD是由两个全等的等边三角形ABD和CBD组成，M、N分别是BC和AD的中点.求证：四边形BMDN是矩形练习 课堂小结1、说说你的收获。2、说说你的困惑。3、说说你的方法。 作业（一）习题1.6知识技能1、2、3联系拓广4（二）如图，四边形ABCD中，对角线相交于点O，E、F、G、H分别是AD，BD，BC，AC的中点。（1）求证：四边形EFGH是平行四边形；（2）当四边形ABCD满足一个什么条件时，四边形EFGH是矩形？并证明你的结论。 谢谢！