八年级数学上册第2章三角形2-2命题与证明第3课时命题的证明教学课件（新版）湘教版

八年级数学上册第2章三角形2-2命题与证明第3课时命题的证明教学课件（新版）湘教版

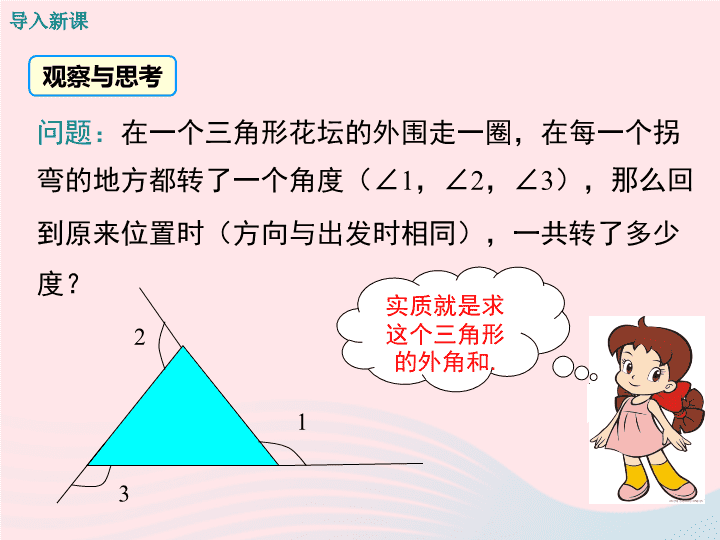
2.2命题与证明第2章三角形导入新课讲授新课当堂练习课堂小结第3课时命题的证明 1.了解证明的基本步骤和书写格式;（重点）2.掌握反证法证明的基本步骤和格式；（难点）3.掌握三角形外角和定理的证明，并能进行简单的运用.学习目标 导入新课观察与思考问题：在一个三角形花坛的外围走一圈，在每一个拐弯的地方都转了一个角度（∠1，∠2，∠3），那么回到原来位置时（方向与出发时相同），一共转了多少度？123实质就是求这个三角形的外角和. 讲授新课证明的一般步骤一活动1：采用剪拼的方法，猜测“三角形的外角和”等于多少度.猜测：三角形的三个外角之和等于360°. 活动2：采用度量的方法，猜测“三角形的外角和”等于多少度.猜测：三角形的三个外角之和等于360°.312∠3≈138.2∠1≈105.6∠2≈118.5 从剪拼或度量可以猜测三角形的三个外角之和等于360°，但是剪拼时难以真正拼成一个周角，只是接近周角；分别度量这三个角后再相加，结果可能接近360°，但不能很准确地都得到360°.思考：怎么证明“三角形的外角和为360°”呢？ 已知：如图，∠BAF，∠CBD和∠ACE分别是△ABC的三个外角.求证：∠BAF+∠CBD+∠ACE=360°.证明猜想 证明：如图，∵∠BAF=∠2+∠3，∴∠BAF+∠CBD+∠ACE=2(∠1+∠2+∠3).∠CBD=∠1+∠3，∠ACE=∠1+∠2，∵∠1+∠2+∠3=180°(三角形内角和定理)，∴∠BAF+∠CBD+∠ACE=2×180°=360°. 证明与图形有关的命题时，一般有以下步骤：第一步第二步第三步画出图形写出已知、求证写出证明的过程根据题意根据命题的条件和结论，结合图形通过分析，找出证明的途径总结归纳 例1已知：如图，在△ABC中，∠B=∠C，点D在线段BA的延长线上，射线AE平分∠DAC.求证：AE∥BC.证明：∵∠DAC=∠B+∠C（三角形外角定理），∠B=∠C（已知），∴∠DAC=2∠B（等式的性质）.又∵AE平分∠DAC（已知），∴∠DAC=2∠DAE（角平分线的定义）∴∠DAE=∠B（等量代换）.∴AE∥BC（同位角相等，两直线平行）典例精析 例2已知：∠A，∠B，∠C是△ABC的内角.求证：∠A，∠B，∠C中至少有一个角大于或等于60°.解析：这个命题的结论是“至少有一个”，也就是说可能出现“有一个”“有两个”“有三个”这三种情况.如果直接来证明，将很繁琐，因此，我们将从另外一个角度来证明.反证法二 证明：假设∠A，∠B，∠C中没有一个角大于或等于60°，即∠A＜60°，∠B＜60°，∠C＜60°，则∠A+∠B+∠C＜180°.这与“三角形的内角和等于180°”矛盾，所以假设不正确.因此，∠A，∠B，∠C中至少有一个角大于或等于60°. 像这样，先假设命题不成立，然后利用命题的条件或有关的结论，通过推理导出矛盾，从而得出假设不成立，即所证明的命题正确，这种证明方法称为反证法.反证法是一种间接证明的方法，其基本的思路可归结为“否定结论，导出矛盾，肯定结论”.总结归纳 应用反证法的情形：(1)直接证明困难;(2)需分成很多类进行讨论;(3)结论为“至少”、“至多”、“有无穷多个”的一类命题；(4)结论为“唯一”类命题. 用反正法证明时，导出矛盾的几种可能：（1）与原命题的条件矛盾；（3）与定义、公理、定理、性质矛盾；（2）与假设矛盾;（4）与客观事实矛盾. 命题“三角形中最多只有一个内角是直角”的结论的否定是()A．两个内角是直角B．有三个内角是直角C．至少有两个内角是直角D．没有一个内角是直角练一练C【解析】“最多只有一个”即为“至多一个”，反设应为“至少有两个”，故应选C. 原词语否定词原词语否定词等于任意的是至少有一个都是至多有一个大于至少有n个小于至多有n个对所有x成立对任何x不成立不是不都是不大于不小于一个也没有至少有两个至多有（n-1)个至少有（n+1)个存在某个x不成立存在某个x,成立不等于某个填一填 当堂练习1.在括号内填上理由.已知：如图，∠A+∠B=180°.求证：∠C+∠D=180°.证明：∵∠A+∠B=180°（已知），∴AD∥BC（）.∴∠C+∠D=180°（）.同旁内角互补，两直线平行两直线平行，同旁内角互补 2．应用反证法推出矛盾的推导过程中，要把下列哪些作为条件使用()①结论相反判断，即假设　②原命题的结论③公理、定理、定义等　　④原命题的条件A．①④B．①②③C．①③④D．②③C 3.已知：如图，直线AB，CD被直线MN所截，∠1=∠2.求证：∠2=∠3，∠3+∠4=180°.证明：∵∠1=∠2，∴∠2=∠3（两直线平行,内错角相等）∠3+∠4=180°（两直线平行,同旁内角互补）.∴AB∥CD（同位角相等，两直线平行） 4.已知：如图，AB与CD相交于点E.求证：∠A+∠C=∠B+∠D.证明：∵AB与CD相交于点E，∴∠AEC=∠BED（对顶角相等），又∵∠A+∠C+∠AEC=∠B+∠D+∠BED=180°（三角形内角和等于180°），∴∠A+∠C=∠B+∠D. 5.求证：△ABC中不能有两个钝角．证明：假设△ABC中能有两个钝角，即∠A＜90°，∠B＞90°，∠C＞90°，所以∠A＋∠B＋∠C＞180°，与三角形的内角和为180°矛盾，所以假设不成立，因此原命题正确，即△ABC中不能有两个钝角． 课堂小结命题的证明直接证明反证法反设结论推理导出矛盾（画图）写出已知、求证写出证明过程证得结论