八年级上数学课件- 13-1-2 线段的垂直平分线的性质 课件（共23张PPT）_人教新课标

八年级上数学课件- 13-1-2 线段的垂直平分线的性质 课件（共23张PPT）_人教新课标

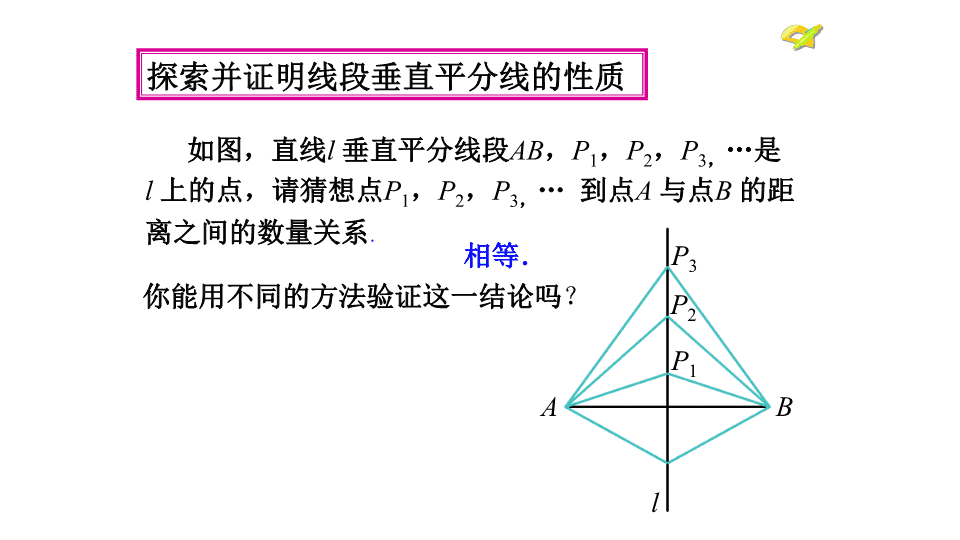
13.1.2线段的垂直平分线的性质人教2011课标版数学八年级上册第十三章轴对称 1.前面我们学习了轴对称图形，线段是轴对称图形吗？什么是线段的垂直平分线2.你能找出线段的对称轴吗？3.线段的对称轴与这条线段有什么关系？说明理由．创设情境，温故知新 你能用不同的方法验证这一结论吗？探索并证明线段垂直平分线的性质如图，直线l垂直平分线段AB，P1，P2，P3，…是l上的点，请猜想点P1，P2，P3，…到点A与点B的距离之间的数量关系．相等．ABlP1P2P3 探索并证明线段垂直平分线的性质请在图中的直线l上任取一点，那么这一点与线段AB两个端点的距离相等吗？线段垂直平分线上的点与这条线段两个端点的距离相等．ABlP1P2P3 已知：如图，直线l⊥AB，垂足为C，AC=CB，点P在l上．求证：PA=PB．探索并证明线段垂直平分线的性质证明：“线段垂直平分线上的点到线段两端点的距离相等．”ABPCl 探索并证明线段垂直平分线的性质证明：∵l⊥AB，∴∠PCA=∠PCB．又AC=CB，PC=PC，∴△PCA≌△PCB（SAS）∴PA=PB．ABPCl已知：如图，直线l⊥AB，垂足为C，AC=CB，点P在l上．求证：PA=PB． 探索并证明线段垂直平分线的性质用几何语言表示为：∵CA=CB，l⊥AB或∵点P在线段AB的垂直平分线上∴PA=PB．∴PA=PB．ABPCl线段垂直平分线的性质：线段垂直平分线上的点与这条线段两个端点的距离相等． 解：AB=AC=CE,AB+BD=DE.∵AD⊥BC，BD=DC∴AB=AC∵点C在AE的垂直平分线上∴AC=CE．∴AB=AC=CE例题讲解例1如图，AD⊥BC，BD=DC，点C在AE的垂直平分线上，AB，AC，CE的长度有什么关系？AB+BD与DE有什么关系？ABCDE∵AB=CE，BD=DC∴AB+BD=CD+CE即AB+BD=DE． 练习1因为AD为BC的中垂线，所以。理由：AB＝AC线段垂直平分线上的点与这条线段两个端点的距离相等．BCAD练习2如图,NM是线段AB的中垂线,下列说法正确的有：。①AB⊥MN,②AD=DB，③MN⊥AB，④MD=DN，⑤AB是MN的垂直平分线ABMND①②③课堂练习 例2如图，在△ABC中，已知AC=27，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长等于50，求BC的长.ABCED例题讲解 变式1如图，在△ABC中，已知AC=27，AB的垂直平分线交AB于点D，交AC于点E，BC=23，求△BCE的周长。ABCED例题讲解 变式2如图，在△ABC中，AB的垂直平分线交AB于点D，交AC于点E，已知AD=15，△BCE的周长等于50，求△BAC的周长.ABCED例题讲解 变式3如图，在△ABC中，AB的垂直平分线交AB于点D，交AC于点E，△BCE的周长等于50，△BAC的周长等于80，求AD的长.ABCED例题讲解 探索并证明线段垂直平分线的判定反过来，如果PA=PB，那么点P是否在线段AB的垂直平分线上呢？点P在线段AB的垂直平分线上．已知：如图，PA=PB．求证：点P在线段AB的垂直平分线上． 探索并证明线段垂直平分线的判定证明：如图，作PC⊥AB则∠PCA=∠PCB=90°．在Rt△PCA和Rt△PCB中，∵PA=PB，PC=PC，∴Rt△PCA≌Rt△PCB（HL）．∴AC=BC．又PC⊥AB，∴点P在线段AB的垂直平分线上已知：如图，PA=PB．求证：点P在线段AB的垂直平分线上． 探索并证明线段垂直平分线的判定用几何符号表示为：∵PA=PB，∴　点P在AB的垂直平分线上．线段垂直平分线的判定与一条线段两个端点距离相等的点，在这条线段的垂直平分线上． 这些点能组成什么几何图形？探索并证明线段垂直平分线的判定你能再找一些到线段AB两端点的距离相等的点吗？能找到多少个到线段AB两端点距离相等的点？在线段AB的垂直平分线l上的点与A，B的距离都相等；反过来，与A，B的距离相等的点都在直线l上，所以直线l可以看成与两点A、B的距离相等的所有点的集合．ABPCl 解：直线AM是线段BC的垂直平分线.∵AB=AC，∴　点A在BC的垂直平分线上．∵MB=MC，∴点M在BC的垂直平分线上∴　直线AM是线段BC的垂直平分线．例3如图，AB=AC，MB=MC．直线AM是线段BC的垂直平分线吗？ABCDM例题讲解 例4已知:如图,在ΔABC中,边AB，BC的垂直平分线交于P.（1）求证：PA=PB=PC;（2）点P是否也在边AC的垂直平分线上呢？由此你还能得出什么结论？BACMNM’N’P例题讲解PA=PB=PCPA=PB点P在线段AB的垂直平分线上分析：PB=PC点P在线段BC的垂直平分线上 结论：三角形三边垂直平分线交于一点，这一点到三角形三个顶点的距离相等。例题讲解例4已知:如图,在ΔABC中,边AB，BC的垂直平分线交于P.（1）求证：PA=PB=PC;（2）点P是否也在边AC的垂直平分线上呢？由此你还能得出什么结论？证明：∵点P在线段AB的垂直平分线MN上，∴PA=PB.同理PB=PC.∴PA=PB=PC.∵PA=PC.∴点P在线段AC的垂直平分线上BACMNM’N’P （1）本节课学习了哪些内容？（2）线段垂直平分线的性质和判定是如何得到的？两者之间有什么关系？（3）如何判断一条直线是否是线段的垂直平分线？课堂小结 二、逆定理：到线段两个端点距离相等的点，在这条线段的垂直平分线上。一、性质定理：线段垂直平分线上的点到这条线段两个端点的距离相等。PA=PB点P在线段AB的垂直平分线上到线段两个端点距离相等的点，在这条线段的垂直平分线上线段垂直平分线上的点到这条线段两个端点的距离相等三、线段的垂直平分线的集合定义：线段的垂直平分线可以看作是到线段两上端点距离相等的所有点的集合.课堂小结 布置作业教科书习题13.1第6、9题．