- 2021-10-26 发布 |
- 37.5 KB |
- 4页


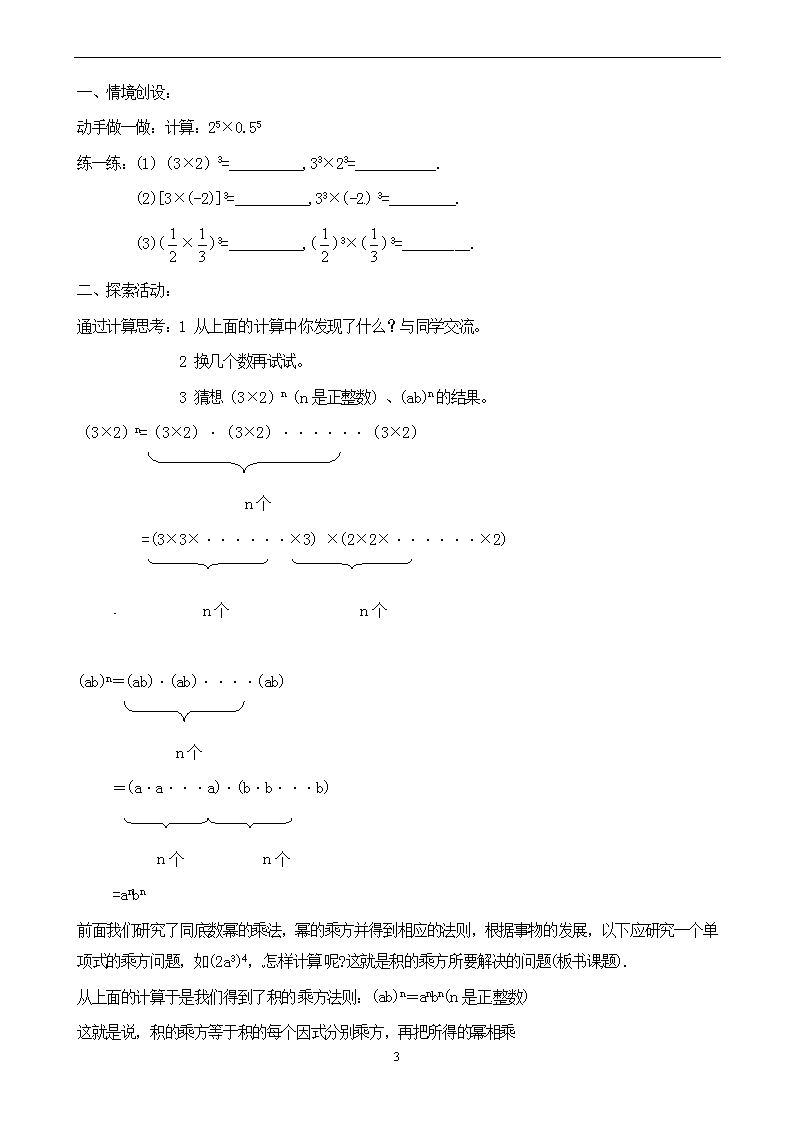
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
幂的乘方与积的乘方教案(1)
8.2幂的乘方与积的乘方(一) 学习目标 1.能说出幂的乘方的运算性质,并会用符号表示; 2.使学生能运用幂的乘方法则进行计算,并能说出每一步运算的依据; 3.在推导幂的乘方法则过程中,培养学生逻辑思维和分析问题的能力; 4.经历探索幂的乘方的运算性质过程,进一步体会幂的意义,从中感受具体到抽象、特殊到一般的思考方法,发展数感和归纳能力。 学习重点:理解并掌握幂的乘方法则. 学习难点:幂的乘方法则的灵活运用. 教学过程 一、情境引入: 一个正方体的边长是102cm,则它的体积是多少? 请一位同学在黑板上写下100个104的乘积,谁能有简便的写法呢?根据乘方的定义,100个104相乘,可以写成(104)100。你会计算吗? 二、探究学习: 1.尝试:做一做:先说出下列各式的意义,再计算下列各式,并说明每一步计算的理由: ⑴ (62)4= ⑵ (a2)3 = ⑶ (am)2= (4)(am)n= 问题:从上面的计算中,你发现了什么规律? 分析:让学生回到定义中去,进而在由同底数幂的乘法法则得出结果,比较后易找找规律。 2.概括总结.上面各式括号中都是幂的形式,然后再乘方.请你给这种运算起个名字。(板书课题:幂的乘方)我们今天就学习它的性质 3.概念巩固:一般地有, 于是得(am)n = am n(m,n都是正整数) 这就是说,幂的乘方,底数不变,指数相乘.(引导学生自己归纳此法则) 法则说明: 1.公式中的底数a可以是具体的数,也可以是代数式. 2.注意幂的乘方中指数相乘,而同底数幂的乘法中是指数相加. 4.典型例题: 例 1: 计算: (1)(106)2; (2)(am)4(m为正整数); (3)-(y3)2; (4)(-x3)3. 4 ⑸ [(x-y)2]3; ⑹ [(a3)2]5. 第(1)、(2)小题由学生口答,教师板演;第(3),(4)(5),(6)学生先思考,再板演。注意符号和乘方的关系. 巩固练习:P44 练一练 1(学生板演)练一练 2 例 2: 计算: (1) x2·x4+(x3)2; (2) (a3)3·(a4)3. 练习:P44 练一练 3,4(学生板演) 四、 思 维 拓 展: 1 填空:(1)108=( )2;(2)b27=(b3)( );(3)(ym)3=( )m;(4)p2nn+2=( )2. 2、请你比较340与430的大小。 三、归纳总结: 1 说说幂的乘方的运算性质; 2 通过探索幂的乘方运算性质的活动,你有什么感受? 3 举例说明幂的乘方运算性质与同底数幂的乘法性质的联系与区别。 8.2 幂的乘方和积的乘方(二) 教学目标: 1经历积的乘方运算性质的探索过程,进一步理解幂的意义; 2使学生能灵活地运用积的乘方法则进行计算,并会解决一些实际问题; 3通过法则的推导过程培养学生分析问题、解决问题的能力; 4 从中感受具体到抽象、特殊到一般的思考方法,发展数感和归纳的能力。 教学重点: 法则的理解与掌握。 教学难点: 法则的灵活运用。 教学方法:引导探索法,学生讨论交流 教学过程: 4 一、情境创设: 动手做一做:计算:25×0.55 练一练:(1)(3×2)3=__________,33×23=___________. (2)[3×(-2)]3=__________,33×(-2) 3=_________. (3)(×)3=__________,()3×()3=_________. 二、探索活动: 通过计算思考:1 从上面的计算中你发现了什么?与同学交流。 2 换几个数再试试。 3 猜想(3×2)n(n是正整数)、(ab)n的结果。 (3×2)n=(3×2)·(3×2)······(3×2) n个 =(3×3×······×3) ×(2×2×······×2) n个 n个 (ab)n=(ab)·(ab)····(ab) n个 =(a·a···a)·(b·b···b) n个 n个 =anbn 前面我们研究了同底数幂的乘法,幂的乘方并得到相应的法则,根据事物的发展,以下应研究一个单项式的乘方问题,如(2a3)4,怎样计算呢?这就是积的乘方所要解决的问题(板书课题). 从上面的计算于是我们得到了积的乘方法则:(ab)n=anbn(n是正整数) 这就是说,积的乘方等于积的每个因式分别乘方,再把所得的幂相乘 4 引导学生剖析积的乘方法则 (1)三个或三个以上的积的乘方,也具有这一性质,如(abc)n=anbncn (2)a,b与前面几个公式一样,可以表示具体的数,也可以表示一个代数式 三、例题教学: 例1 计算: (1)(5m )3; (2)(-xy2)3; 解:(1)(5m)3=53·m3=125m3; (2)(- xy2)3=(-1)3·x3·(y2)3=-x3y6. 第(1)小题由学生回答,教师板演,并要求学生说出每一步的根据是什么;第(2)小题由学生板演,根据学生板演的情况,提醒学生注意:(1)系数的乘方;(2)因数中若有幂的形式,要注意运算步骤,先进行积的乘方,后作因数幂的乘方 例2 计算: (1)(3xy2)2; (2)(-2ab3c2)4 解:(1)(3xy2)2=32·x2·(y2)2=9x2y4; (2)(-2ab3c2)4 =(-2)4·a4·(b3)4·(c2)4=16a4b12c8. 先由学生观察、讨论解题的方法,然后由教师根据学生的回答板书,并要求说出运算中每一步的依据. 课堂练习:练一练 1、3、4 四、思维拓展: 计算:(-1/4)4×210,并说明计算的理由。 四、小结: 1、 掌握积的乘方的运算法则,注意积的乘方要将每一个因式(特别是系数)都要乘方。 2、 灵活地双向应用运算性质,使运算更加方便、简洁。 4查看更多