七年级下册数学教案5-1-2 垂线 1 人教版

七年级下册数学教案5-1-2 垂线 1 人教版

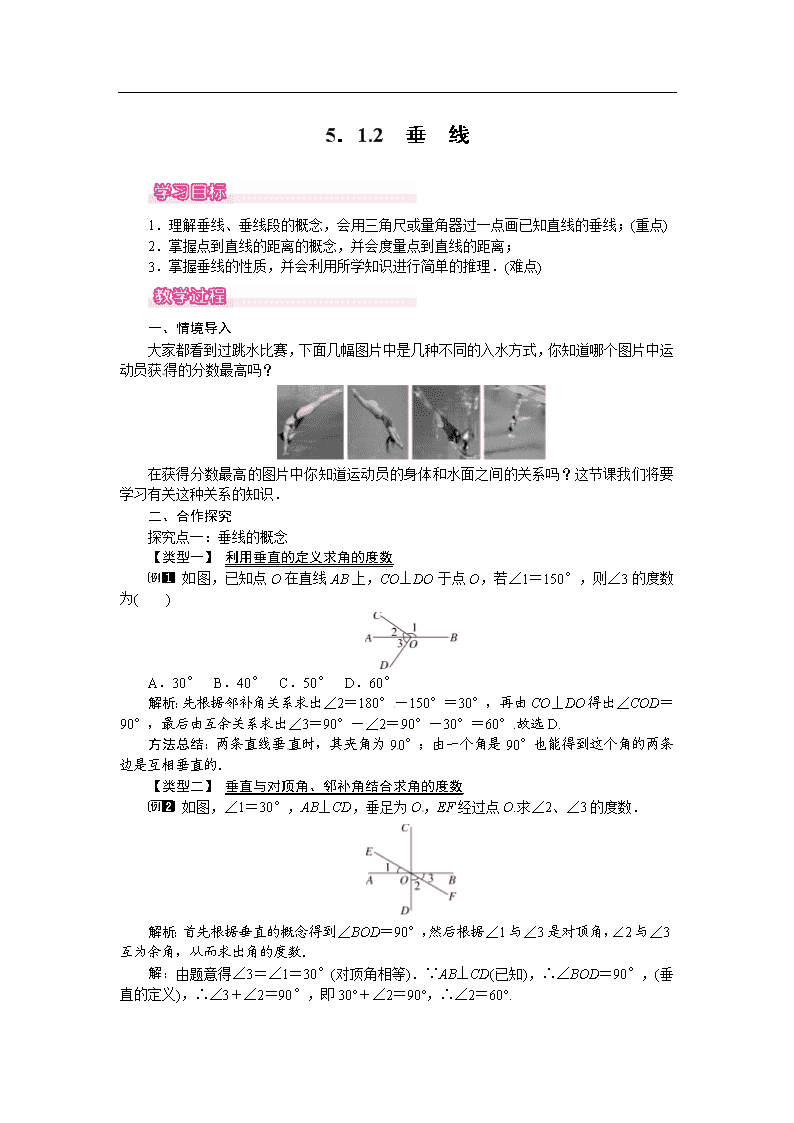
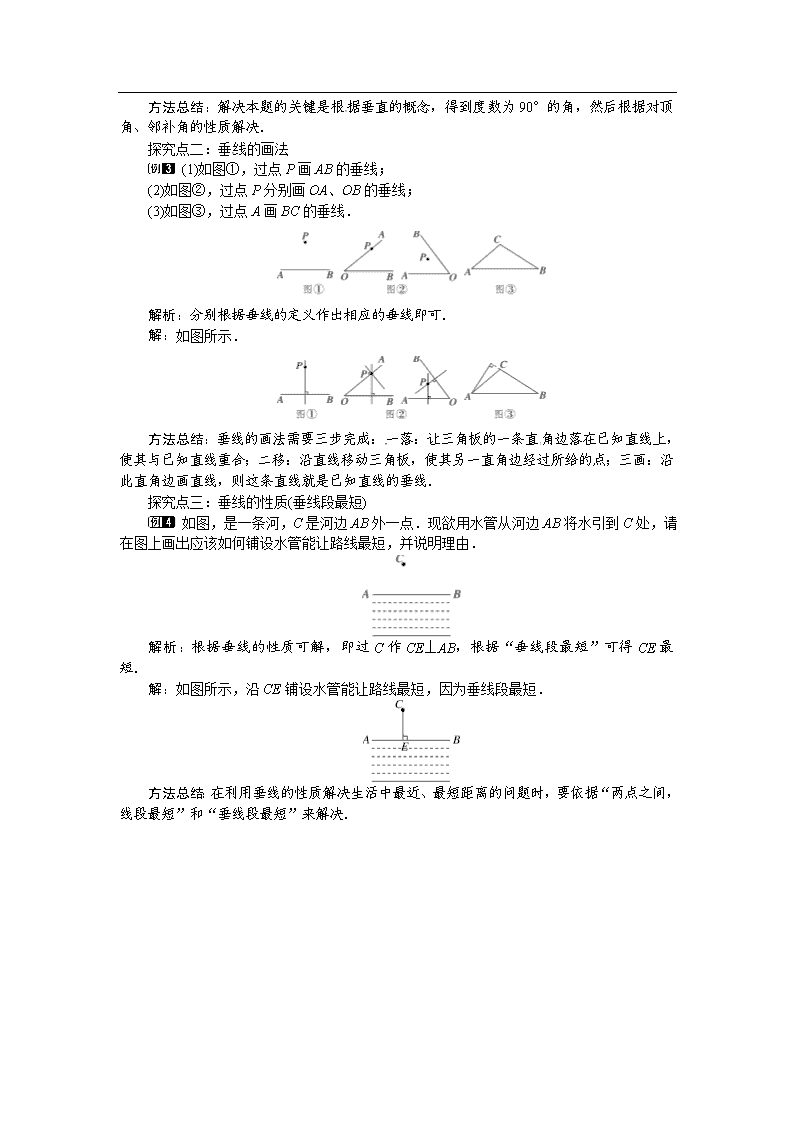
‎5．1.2　垂　线 ‎　　　　　　　　　　　　　　　　　‎ ‎1．理解垂线、垂线段的概念，会用三角尺或量角器过一点画已知直线的垂线；(重点)‎ ‎2．掌握点到直线的距离的概念，并会度量点到直线的距离；‎ ‎3．掌握垂线的性质，并会利用所学知识进行简单的推理．(难点)‎ 一、情境导入 大家都看到过跳水比赛，下面几幅图片中是几种不同的入水方式，你知道哪个图片中运动员获得的分数最高吗？‎ 在获得分数最高的图片中你知道运动员的身体和水面之间的关系吗？这节课我们将要学习有关这种关系的知识．‎ 二、合作探究[来源:学科网]‎ 探究点一：垂线的概念 ‎【类型一】 利用垂直的定义求角的度数 ‎ 如图，已知点O在直线AB上，CO⊥DO于点O，若∠1＝150°，则∠3的度数为(　　)‎ A．30° B．40° C．50° D．60°‎ 解析：先根据邻补角关系求出∠2＝180°－150°＝30°，再由CO⊥DO得出∠COD＝90°，最后由互余关系求出∠3＝90°－∠2＝90°－30°＝60°.故选D.‎ 方法总结：两条直线垂直时，其夹角为90°；由一个角是90°也能得到这个角的两条边是互相垂直的．‎ ‎【类型二】 垂直与对顶角、邻补角结合求角的度数 ‎ 如图，∠1＝30°，AB⊥CD，垂足为O，EF经过点O.求∠2、∠3的度数．‎ 解析：首先根据垂直的概念得到∠BOD＝90°，然后根据∠1与∠3是对顶角，∠2与∠3互为余角，从而求出角的度数．‎ 解：由题意得∠3＝∠1＝30°(对顶角相等)．∵AB⊥CD(已知)，∴∠BOD＝90°，(垂直的定义)，∴∠3＋∠2＝90°，即30°＋∠2＝90°，∴∠2＝60°.‎ 方法总结：解决本题的关键是根据垂直的概念，得到度数为90°的角，然后根据对顶角、邻补角的性质解决．‎ 探究点二：垂线的画法 ‎ (1)如图①，过点P画AB的垂线；[来源:学科网]‎ ‎(2)如图②，过点P分别画OA、OB的垂线；‎ ‎(3)如图③，过点A画BC的垂线．‎ 解析：分别根据垂线的定义作出相应的垂线即可．‎ 解：如图所示．‎ 方法总结：垂线的画法需要三步完成：一落：让三角板的一条直角边落在已知直线上，使其与已知直线重合；二移：沿直线移动三角板，使其另一直角边经过所给的点；三画：沿此直角边画直线，则这条直线就是已知直线的垂线．[来源:Z&xx&k.Com]‎ 探究点三：垂线的性质(垂线段最短)‎ ‎ 如图，是一条河，C是河边AB外一点．现欲用水管从河边AB将水引到C处，请在图上画出应该如何铺设水管能让路线最短，并说明理由．[来源:Zxxk.Com]‎ 解析：根据垂线的性质可解，即过C作CE⊥AB，根据“垂线段最短”可得CE最短．‎ 解：如图所示，沿CE铺设水管能让路线最短，因为垂线段最短．‎ 方法总结：在利用垂线的性质解决生活中最近、最短距离的问题时，要依据“两点之间，线段最短”和“垂线段最短”来解决．‎ 探究点四：点到直线的距离 ‎ 如图，在△ABC中，过点C作CD⊥AB，垂足为D，则点C到直线AB的距离是(　　)‎ A．线段CA的长 B．线段CD C．线段AD的长 D．线段CD的长 解析：根据点到直线的距离的定义：直线外一点到直线的垂线段的长度叫做点到直线的距离，可得点C到直线AB的距离是线段CD的长．故选D.‎ 方法总结：点到直线的距离是直线外一点到直线的垂线段的长度，而不是垂线段．‎ 三、板书设计 垂线 ‎[来源:Zxxk.Com]‎ ‎ 本节课主要研究两条直线相交时的特殊情况——垂直，可类比前面两条直线相交时的一般情况学习新知识．经历合作探究过程获得新知，并能用所学的新知识来解决实际问题．这样教学更能激发学生学习数学的兴趣，使每个学生在数学的学习上都能得到不同的发展