人教版七年级下册数学全册导学案
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
1
第 1 课时:5.1.1 相交线 导学案
【学习目标】1、了解邻补角、对顶角, 能找出图形中的一个角的邻补角和对顶角
2、理解对顶角相等,并能运用它解决一些问题.
【学习重点】邻补角、对顶角的概念,对顶角性质与应用.
【学习难点】理解对顶角相等的性质.
【学习过程】
一、温故知新(5 分钟)
各小组对七年级上学过的直线、射线、线段、角做总结.每人写一个总结小报告,并编写两道与它们相关的
题目,在小组交流,并推出小组最好的两道题在班级汇报.
二、自主探索(15 分钟)
探索一:完成课本 P2 页的探究,填在课本上.
你能归纳出“邻补角”的定义吗? .
“对顶角”的定义呢? .
自学检测一:
1.如图 1 所示,直线 AB 和 CD 相交于点 O,OE 是一条射线.
(1)写出∠AOC 的邻补角:____ _ ___ __;
(2)写出∠COE 的邻补角: __;
(3)写出∠BOC 的邻补角:____ _ ___ __;
(4)写出∠BOD 的对顶角:____ _.
2.如图所示,∠1 与∠2 是对顶角的是( )
探索二:任意画一对对顶角,量一量,算一算,它们相等吗?如果相等,请说明理由.
请归纳“对顶角的性质”: .
自学检测二:
1.如图,直线 a,b 相交,∠1=40°,则∠2=_______∠3=_______∠4=_______
2.如图直线 AB、CD、EF 相交于点 O,∠BOE 的对顶角是______,∠COF 的邻补角是____,若∠AOE=30°,那么
∠BOE=_______,∠BOF=_______
3.如图,直线 AB、CD 相交于点 O,∠COE=90°,∠AOC=30°,∠FOB=90°, 则∠EOF=_____.
三、当堂反馈(25 分钟)
预备题:
如图,已知直线 a、b 相交。∠1=40°,求∠2、∠3、∠4 的度数
解:∠3=∠1=40°( )。
∠2=180°-∠1=180°-40°=140°( )。
∠4=∠2=140°( )。
图 1
b
a
4
3
2
1
第 1 题
F
E
O
D
C
B
A
第 2 题
F
E
O
D
C
B
A
第 3 题
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
2
1、如图,已知∠1=30° ,求∠2、∠3∠4 的度数。
2.若两个角互为邻补角,则它们的角平分线所夹的角为 度.
3.如图所示,直线 a,b,c 两两相交,∠1=60°,∠2= 2
3
∠4,求∠3、∠5 的度数.
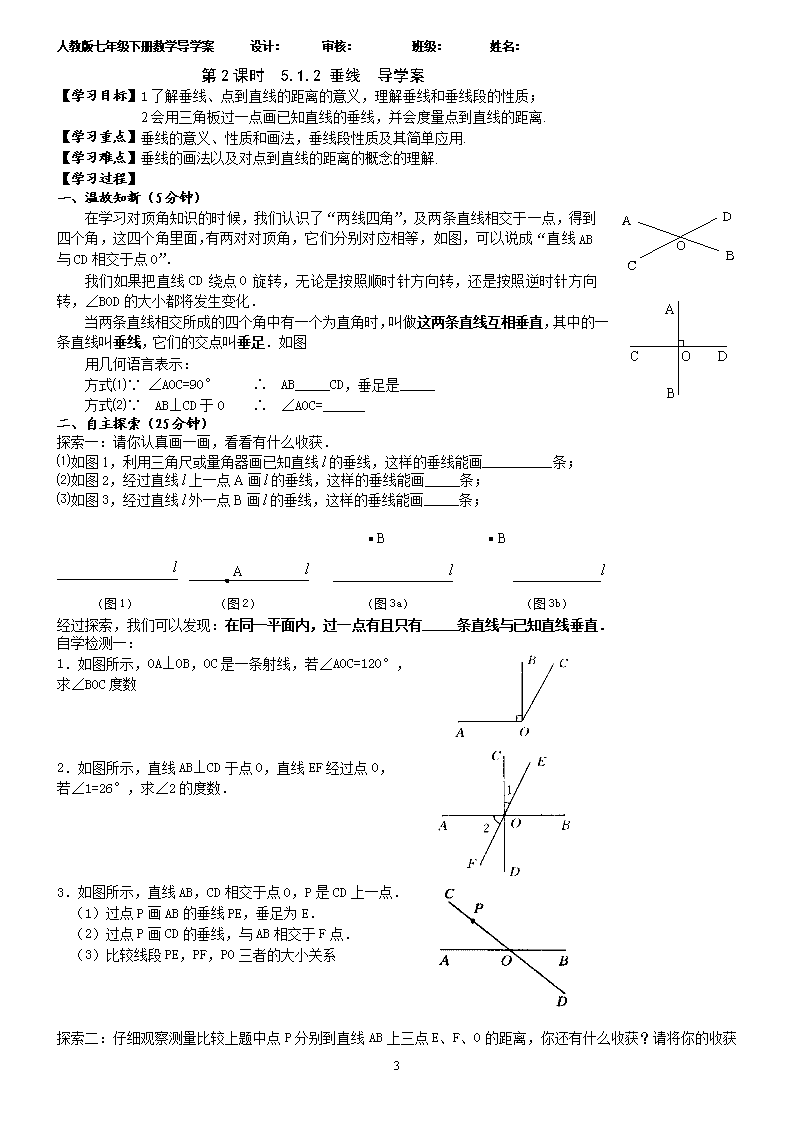
4.如图所示,有一个破损的扇形零件,利用图中的量角器可以量出这个扇形零件的圆心角的度数,你能说出所
量的角是多少度吗?你的根据是什么?
5.探索规律:(画图探究)
(1)两条直线交于一点,有 对对顶角;
(2)三条直线交于一点,有 对对顶角;
(3)四条直线交于一点,有 对对顶角;
(4)n 条直线交于一点,有 对对顶角.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
3
第 2 课时 5.1.2 垂线 导学案
【学习目标】1 了解垂线、点到直线的距离的意义,理解垂线和垂线段的性质;
2 会用三角板过一点画已知直线的垂线,并会度量点到直线的距离.
【学习重点】垂线的意义、性质和画法,垂线段性质及其简单应用.
【学习难点】垂线的画法以及对点到直线的距离的概念的理解.
【学习过程】
一、温故知新(5 分钟)
在学习对顶角知识的时候,我们认识了“两线四角”,及两条直线相交于一点,得到
四个角,这四个角里面,有两对对顶角,它们分别对应相等,如图,可以说成“直线 AB
与 CD 相交于点 O”.
我们如果把直线 CD 绕点 O 旋转,无论是按照顺时针方向转,还是按照逆时针方向转,
∠BOD 的大小都将发生变化.
当两条直线相交所成的四个角中有一个为直角时,叫做这两条直线互相垂直,其中的
一条直线叫垂线,它们的交点叫垂足.如图
用几何语言表示:
方式⑴∵ ∠AOC=90° ∴ AB_____CD,垂足是_____
方式⑵∵ AB⊥CD 于 O ∴ ∠AOC=______
二、自主探索(25 分钟)
探索一:请你认真画一画,看看有什么收获.
⑴如图 1,利用三角尺或量角器画已知直线l 的垂线,这样的垂线能画__________条;
⑵如图 2,经过直线l 上一点 A 画l 的垂线,这样的垂线能画_____条;
⑶如图 3,经过直线l 外一点 B 画l 的垂线,这样的垂线能画_____条;
(图 1) (图 2) (图 3a) (图 3b)
经过探索,我们可以发现:在同一平面内,过一点有且只有_____条直线与已知直线垂直.
自学检测一:
1.如图所示,OA⊥OB,OC 是一条射线,若∠AOC=120°,
求∠BOC 度数
2.如图所示,直线 AB⊥CD 于点 O,直线 EF 经过点 O,
若∠1=26°,求∠2 的度数.
3.如图所示,直线 AB,CD 相交于点 O,P 是 CD 上一点.
(1)过点 P 画 AB 的垂线 PE,垂足为 E.
(2)过点 P 画 CD 的垂线,与 AB 相交于 F 点.
(3)比较线段 PE,PF,PO 三者的大小关系
探索二:仔细观察测量比较上题中点 P 分别到直线 AB 上三点 E、F、O 的距离,你还有什么收获?请将你的收获
O
D
C
B
A
C D
A
B
O
l lA l
B
l
B
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
4
记录下来:_______________________________________________
简单说成: .还有,直线外一点到这条直线的垂线段的 叫做点到直线的距离.注意:
垂线是 ,垂线段是一条 ,点到直线的距离是一个数量,不能说“垂线段”是距离.
自学检测二:
1.在下列语句中,正确的是( ).
A.在同一平面内,一条直线只有一条垂线
B.在同一平面内,过直线上一点的直线只有一条
C.在同一平面内,过直线上一点且垂直于这条直线的直线有且只有一条
D.在同一平面内,垂线段就是点到直线的距离
2.如图所示,AC⊥BC,CD⊥AB 于 D,AC=5cm,BC=12cm,AB=13cm, 则点 B 到 AC 的距离
是________,点 A 到 BC 的距离是_______,点 C 到 AB的距 离 是 _______ ,
AC>CD的依据是_________.
三、当堂反馈(15 分钟)
1.如图所示AB,CD相交于点O,EO⊥AB于O,FO⊥CD于O,∠EOD与 ∠FOB的大小关系是( )
A.∠EOD比∠FOB大 B.∠EOD比∠FOB小
C.∠EOD与∠FOB相等 D.∠EOD与∠FOB大小关系不确定
2.如图,一辆汽车在直线形的公路 AB 上由 A 向 B 行驶,C,D 是 分别位于公路 AB 两侧的
加油站.设汽车行驶到公路 AB 上点 M 的位置时,距离加油站 C 最近;行驶到点 N 的位置时,距离加油站 D 最近,
请在图中的公路上分别画出点 M,N 的位置并说明理由.
3.如图,AOB为直线,∠AOD:∠DOB=3:1,OD平分∠COB.
(1)求∠AOC的度数;(2)判断AB与OC的位置关系.
第 3 课时 5.1.3 同位角、内错角、同旁内角 导学案
【学习目标】1 使学生理解三线八角的意义,并能从复杂图形中识别它们;
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
5
2 通过三线八角的特点的分析,培养学生抽象概括问题的能力.
【学习重点】三线八角的意义,以及如何在各种变式的图形中找出这三类角.
【学习难点】能准确在各种变式的图形中找出这三类角.
【学习过程】
一、温故知新(5 分钟)
在前面我们学习了两条直线相交于一点,得到四个角,即“两线四角”,这四个角里面,有 对对顶角,
有 对邻补角.如果是一条直线分别与两条直线相交,结果又会怎样呢?
二、探索思考(25 分钟)
探索:如图,直线 c 分别与直线 a、b 相交(也可以说两条
直线 a、b 被第三条直线 c 所截),得到 8 个角,通常称为
“三线八角”,那么这 8 个角之间有哪些关系呢?
观察填表: 表一
位置 1 位置 2 结论
∠1 和∠5 处于直线 c 的同侧 处于直线 a、b 的同一方 这样位置的一对角
就称为同位角
∠2 和∠8 处于直线 c 的( )侧 这样位置的一对角
就称为( )
∠3 和∠6 处于直线 a、b 的( )方 这样位置的一对角
就称为( )
∠1 和∠5 这样位置的一对角
就称为( )
表二
位置 1 位置 2 结论
∠4 和∠8 处于直线 c 的两侧 处于直线 a、b 之间 这样位置的一对角
就称为内错角
∠3 和∠5 这样位置的一对角
就称为( )
表三
位置 1 位置 2 结论
∠3 和∠8 处于直线 c 的( )侧 处于直线 a、b( ) 这样位置的一对角
就称为同旁内角
∠4 和∠5 这样位置的一对角
就称为( )
自学检测:
1.如图 1 所示,∠1 与∠2 是__ _角,∠2 与∠4 是_ 角,∠2 与∠3 是__ _角.
a
b
c
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
6
(图 1) (图 2) (图 3)
2.如图 2 所示,∠1 与∠2 是___ _角,是直线______和直线_______被直线_______所截而形成的,∠1 与∠
3 是___ __角,是直线________和直线______被直线________所截而形成的.
3.如图 3 所示,∠B 同旁内角有哪些?
三、当堂反馈(15 分钟)
1.如图,(1)直线 AD、BC 被直线 AC 所截,找出图中由 AD、 BC 被直线 AC 所截
而成的内错角是_________和__________
(2)∠3 和∠4 是直线_________和_________被_________ 所截,构成内错
角.
2.已知∠1 与∠2 是同旁内角,且∠1=60°,则∠2 为( )
A. 60° B. 120° C. 60°或 120° D.无法确定
3.如图,判断正误
①∠1 和∠4 是同位角;( )
②∠1 和∠5 是同位角;( )
③∠2 和∠7 是内错角;( )
④∠1 和∠4 是同旁内角;( )
4.如图,直线 DE、BC 被直线 AB 所截.
⑴∠1 与∠2、∠1 与∠3、∠1 与∠4 各是什么角?
⑵如果∠1=∠4,那么∠1 和∠2 相等吗?∠1 和∠3 互 补吗?为什么?
第 4 课时 5.2.1 平行线 导学案
【学习目标】1 使学生知道平行线的概念,掌握平行公理;
3
4
1
E
2
B
C
D
A
3
4
1
E
2
B
C
D
A
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
7
2 了解平行线具有传递性,能够画出已知直线的平行线.
【学习重点】平行线的概念和平行公理,利用直尺和三角板画已知直线的平行线.
【学习难点】用几何语言描述画图过程,根据几何语言画出图形.
【学习过程】
一、温故知新(5 分钟)
在上学期我们学过点和直线的位置关系,同学们还记得点和直线有几种位置关系吗?请画出来,并尝试用几
何语言来表示.
二、探索思考(25 分钟)
探索一:我们知道,火车行驶的两条笔直的铁轨、人行道上的斑马线 等都给我们平行
的形象.一般地,在同一平面内,不相交的两条直线叫做平行线.如图, 记作“ a ∥ b ”
或“AB∥CD”,读作“直线 a 平行于直线 b ”.请同学们思考一下:在 同一平面内,两
条不重合的直线有几种位置关系?动手画一画,并尝试用几何语言来 表示..
自学检测一:
1.下列说法中,正确的是( ).
A.两直线不相交则平行 B.两直线不平行则相交
C.若两线段平行,那么它们不相交 D.两条线段不相交,那么它们平行
2.在同一平面内,有三条直线,其中只有两条是平行的,那么交点有( ).
A.0 个 B.1 个 C.2 个 D.3 个
探索二:请同学们仔细阅读课本 P13 页“平行线的讨论”,认真思考.通过观察和画图,可以体验一个基本事实(平
行公理):经过直线外一点, 一条直线与这条直线平行.
同样,我们还有(平行线的传递性):如果两条直线都与第三条直线平行,那么这两条直线也互相平行.简单的
说就是:平行于同一直线的两直线平行.
用几何语言可表示为:如果b ∥ a , c ∥ a ,那么 .
自学检测二:
1.如图 1 所示,与 AB 平行的棱有_______条,与 AA′平行的棱有_____条.
(图 1) (图 2)
2.如图 2 所示,按要求画平行线.
(1)过 P 点画 AB 的平行线 EF;(2)过 P 点画 CD 的平行线 MN.
3.如图 3 所示,点 A,B 分别在直线 1l , 2l 上,(1)过点 A 画到 2l 的垂线段;(2)过点 B 画直线 3l ∥ 1l .
(图 3)
4.下列说法中,错误的有( ).
①若 a 与 c 相交,b 与 c 相交,则 a 与 b 相交;
A B
C D
a
b
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
8
②若 a∥b,b∥c,那么 a∥c;
③过一点有且只有一条直线与已知直线平行;
④在同一平面内,两条直线的位置关系有平行、相交、垂线三种
A.3 个 B.2 个 C.1 个 D.0 个
三、当堂反馈(15 分钟)
1.在同一平面内,一条直线和两条平行线中一条直线相交,那么这条直线与平行线中的另一边必__________.
2.同一平面内,两条相交直线不可能与第三条直线都平行,这是因为________________.
3.判断题
(1)不相交的两条直线叫做平行线.( )
(2)在同一平面内,不相交的两条射线是平行线.( )
(3)如果一条直线与两条平行线中的一条平行, 那么它与另一条也互相平行.( )
4.读下列语句,并画出图形:
⑴点 P 是直线 AB 外一点,直线 CD 经过点 P,且与直线 AB 平行,直线 EF 也经过点 P且与直线 AB 垂直.
⑵直线 AB,CD 是相交直线,点 P 是直线 AB,CD 外一点,直线 EF 经过点 P且与直线 AB 平行,与直线 CD 相交于
E.
第 5 课时 5.2.2 平行线的判定 导学案
【学习目标】使学生掌握平行线的判定,并能应用这些知识判断两条直线是否平行,培养学生简单的推理能力.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
9
【学习重点】平行线的三种判定方法,并运用这三种方法判断两直线平行.
【学习难点】运用平行线的判定方法进行简单的推理.
【学习过程】
一、温故知新(5 分钟)
还知道“三线八角”吗?请画一画,找出一组同位角、一组内错角、一组同旁内角.
二、探索思考(25 分钟)
探索一:请同学们仔细阅读课本 P13 页“平行线判定的思考”,你知道在画平行线这一过程中,三角尺所起的作
用吗?
由此我们可以得到平行线的判定方法,如图,将下列空白补充完整(填 1 种就可以)
判定方法 1(判定公理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法 1,结合对顶角的性质,我们可以得到:
判定方法 2(判定定理)
几何语言表述为:∵ ∠___=∠___ ∴ AB∥CD
由判定方法 1,结合邻补角的性质,我们可以得到:
判定方法 3(判定定理)
几何语言表述为:∵ ∠___+∠___=180° ∴ AB∥CD
自学检测一:
(1 题) (2 题) (3 题)
1.如图 1 所示,若∠1=∠2,则_____∥______,根据是__ ____.
若∠1=∠3,则______∥______,根据是_____ ____.
2.如图 2 所示,若∠1=62°,∠2=118°,则_____∥_____,根据是_____ ___
3.根据图 3 完成下列填空(括号内填写定理或公理)
(1)∵∠1=∠4(已知)
∴ ∥ ( )
(2)∵∠ABC +∠ =180°(已知)
∴AB∥CD( )
(3)∵∠ =∠ (已知)
∴AD∥BC( )
(4)∵∠5=∠ (已知)
∴AB∥CD( )
探索二:木工师傅用角尺画出工件边缘的两条垂线,就可以再 找 出 两 条 平 行
线,如图所示, a ∥b ,你能说明是什么道理吗?
结论(判定推论):在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行.简记为:在同一
平面内,垂直于同一直线的两直线平行.
8
3
6
2
5
1
4
7
F
E
D
C
B
A
C
1
2
3
4
5
DA
B
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
10
如图,几何语言表述为:∵ a ⊥ 2l ,b ⊥ 2l ∴
自学检测二:
1.如图所示,AB⊥BC,BC⊥CD,BF 和 CE 是射线,并且∠1=∠2,
试说明 BF∥CE.
三、当堂反馈(15 分钟)
1.如图所示,在下列条件中,不能判断 L1∥L2 的是( ).
A.∠1=∠3 B.∠2=∠3
C.∠4+∠5=180° D.∠2+∠4=180°
2.如图所示,已知∠1=120°,∠2=60°.试说明 a 与b 的关系?
3.如图所示,已知∠OEB=130°,∠FOD=25°,OF 平分∠EOD,试说明 AB∥CD.
第 6 课时 5.3.1 平行线的性质 导学案
a b
c
1 2
a b
3
c
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
11
【学习目标】1 使学生掌握平行线的三个性质,并能应用它们进行简单的推理论证;
2 使学生经过对比后,理解平行线的性质和判定的区别和联系.
【学习重点】平行线的三个性质及其应用.
【学习难点】正确理解性质与判定的区别和联系,并正确运用它们去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理 1:
⑸平行线的判定定理 2:
⑹平行线的判定推论:
二、探索思考
探索一:请同学们仔细阅读课本 P19 页,完成课本上的探究.根据探究内容,我们可以得到平行线的性质,如图,
将下列空白补充完整(填 1 种就可以)
性质 1(性质公理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质 1,结合对顶角的性质,我们可以得到:
性质 2(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___=∠___
由性质 1,结合邻补角的性质,我们可以得到:
性质 3(性质定理)
几何语言表述为:∵ AB∥CD ∴ ∠___+∠___=
练习一:
1. 根据右图将下列几何语言补充完整
(1)∵AD∥ (已知)
∴∠A+∠ABC=180°( )
(2)∵AB∥ (已知)
∴∠4=∠ ( )
∠ABC=∠ ( )
2. 如右图所示,BE 平分∠ABC,DE∥ BC,图中相等的角共有( )
A. 3 对 B. 4 对 C. 5 对 D. 6 对
3、如图,AB∥CD,∠1=45°,∠D=∠C,求∠D、∠C、∠B 的度数.
探索二:用三角尺和直尺画平行线
做成一张 5×5 个格子的方格纸.观察做出的方格纸的一部分(如图),线段
11CB 、 22CB 、…、 55CB 都与两条平行的横线 51BA 和 52CA 垂直吗?
它们的长度相等吗?
像这样,同时垂直于两条平行直线,并且夹在
这两条平行线间的线段的长度相等,叫做这两条平行线间的距离,即平行线
间的距离处处相等.
练习二:
1.如图所示,已知直线 AB∥CD,且被直线 EF 所截,若∠1=50°,则∠2=____,
8
3
6
2
5
1
4
7
F
E
D
C
B
A
C
1 2
3
4
5B
D
ED
CB
A
1A
2A
1B 2B 3B 4B 5B
1C 2C 3C 5C4C
A
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
12
∠3=______.
(1 题) (2 题) (3 题)
2.如图所示,AB∥CD,AF 交 CD 于 E,若∠CEF=60°,则∠A=______.
3.如图所示,已知 AB∥CD,BC∥DE,∠1=120°,则∠2=______.
三、当堂反馈
1.如图所示,如果 AB∥CD,那么( ).
A.∠1=∠4,∠2=∠5 B.∠2=∠3,∠4=∠5
C.∠1=∠4,∠5=∠7 D.∠2=∠3,∠6=∠8
(1 题) (2 题) (3 题)
2.如图所示,DE∥BC,EF∥AB,则图中和∠BFE 互补的角有( ).
A.3 个 B.2 个 C.5 个 D.4 个
3.如图所示,已知∠1=72°,∠2=108°,∠3=69°,求∠4 的度数.
4.如图所示,已知 AB∥CD,∠ABE=130°,∠CDE=152°,求∠BED 的度数.
E
DC
BA
5.如图所示,∠1=72°,∠2=72°,∠3=60°,求∠4 的度数
b a
3
4
1 2
第 7 课时 平行线的判定及性质习题课 导学案
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
13
【学习目标】加深对平行线的判定及性质的理解及其应用.
【学习重点】平行线的判定及性质的应用.
【学习难点】灵活运用平行线的判定及性质去推理证明.
【学习过程】
一、学前准备
通过前面的学习,你知道判定两条直线平行有哪几种方法吗?
⑴平行线的定义:
⑵平行线的传递性:
⑶平行线的判定公理:
⑷平行线的判定定理 1:
⑸平行线的判定定理 2:
⑹平行线的判定推论:
通过前面的学习,你还知道两条直线平行有哪些性质吗?
⑴根据平行线的定义:
⑵平行线的性质公理:
⑶平行线的性质定理 1:
⑷平行线的性质定理 2:
⑸平行线间的距离 .
二、探索思考
练习:让我先试试,相信我能行.
1.如图 1,若∠1=∠2,那么_____∥______,根据___ __.
若 a∥b,那么∠3=_____,根据___ __.
(图 1) (图 2) (图 3) (图 4)
2.如图 2,∵∠1=∠2,∴_______∥_______,根据___ _____.
∴∠B=______,根据___ _____.
3.如图 3,若 AB∥CD,那么________=_______;若∠1=∠2,那么_____∥_____;
若 BC∥AD,那么_______=_______;若∠A+∠ABC=180°,那么______∥_____
4.如图 4,一条公路两次拐弯后,和原来的方向相同,如果第一次拐的角是 136°(即∠ABC),那么第二次
拐的角(∠BCD)是 度,根据___ .
5.如图,修高速公路需要开山洞,为节省时间,要在山两面 A,B
同时开工,在 A 处测得洞的走向是北偏东 76°12′,那么在 B 处
应按什么方向开口,才能使山洞准确接通,请说明其中的道理.
6.如图所示,潜望镜中的两个镜子是互相平行放置的,光线经过
镜子反射∠1=∠2,∠3=∠4,请你解释为什么开始进入潜望镜的光
线和最后离开潜望镜的光线是平行的.
三、当堂反馈
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
14
1.已知如图 1,用一吸管吸吮易拉罐内的饮料时,吸管与易拉罐上部夹角∠1=74°,那么吸管与易拉罐下部夹
角∠2=_______.
2.已知如图 2,边 OA,OB 均为平面反光镜,∠AOB=40°,在 OB 上有一点 P,从 P 点射出一束光线经 OA 上的 Q
点反射后,反射光线 QR 恰好与 OB 平行,则∠QPB 的度数是( ).
A.60° B.80° C.100° D.120°
(图 1) (图 2) (图 3)
3.如图 3,已知∠1+∠2=180°,∠3=∠B,试判断∠AED 与∠C 的大小关系,并对结论进行说理.
4.如图,直线 DE 经过点 A,DE∥BC,∠B=44°,∠C=85°.⑴求∠DAB 的度数;⑵求∠EAC 的度数;⑶求∠BAC
的度数;⑷通过这道题你能说明为什么三角形的内角和是 180°吗?
5.若两条平行线被第三条直线所截,则一组同位角的平分线互相( )
A.垂直 B.平行 C.重合 D.相交
6.如图 3 所示,CD∥AB,OE 平分∠AOD,OF⊥OE,∠D=50°,则∠BOF 为( )
A.35° B.30° C.25° D.20°
7.如图 4 所示,AB∥CD,则∠A+∠E+∠F+∠C 等于( )
A.180° B.360° C.540° D.720°
O
FE DC
BA F
E
DC
BA
G
FE
D C
BA
1
F E
D CB
A
(3) (4) (5) (6)
8.如图 5 所示,AB∥EF∥CD,EG∥BD,则图中与∠1 相等的角(∠1 除外)共有( )
A.6 个 B.5 个 C.4 个 D.3 个
9.如图 6 所示,如果 DE∥AB,那么∠A+______=180°,或∠B+_____=180°,根据是______;如果
∠CED=∠FDE,那么________∥_________.根据是________.
第 8 课时 5.3.2 命题、定理 导学案
AD E
B C
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
15
【学习目标】了解命题、定理的概念,能够区分命题的题设和结论.
【学习重点】能够区分命题的题设和结论.
【学习难点】能够区分命题的题设和结论.
【学习过程】
一、探索思考
探索:在日常生活中,我们会遇到许多类似的情况,需要对一些事情作出判断,例如:
⑴今天是晴天;⑵对顶角相等;⑶如果两条直线都与第三条直线平行,那么这两条直线也互相平行.像这样,判
断一件事情的语句,叫做命题.
每个命题都是由_______和______组成.每个命题都可以写成.“如果……,那么……”的形式,用“如果”
开始的部份是 ,用“那么”开始的部份是 .
像前面举例中的⑵⑶两个命题,都是正确的,这样的命题叫做真命题,即正确的命题叫做______.
例如:“如果一个数能被 2 整除,那么这个数能被 4 整除”,很明显是错误的命题,这样的命题叫做假命题,
即错误的命题叫做______.
我们把从长期的实践活动中总结出来的正确命题叫做公理;通过正确的推理得出的真命题叫做定理.
二、学以致用
1.下列语句是命题的个数为( )
①画∠AOB 的平分线; ②直角都相等; ③同旁内角互补吗? ④若│a│=3,则 a=3.
A.1 个 B.2 个 C.3 个 D.4 个
2.下列 5 个命题,其中真命题的个数为( )
①两个锐角之和一定是钝角; ②直角小于夹角; ③同位角相等,两直线平行;
④内错角互补,两直线平行; ⑤如果 a
0,则点 P 在( )
A.第一象限 B. 第二象限 C. 第三象限 D. 第一象限和第三象限
5.已知点 A(m,-2),点 B(3,m-1),且直线 AB∥x 轴,则 m 的值为( )
A.3 B.1 C.0 D.-1
6.平面内点的坐标是( )
A.一个点 B.一个图形 C.一个数 D.一个有序数对
7.在平面直角坐标系内,下列说法错误的是( )
A.原点 O 不在任何象限内 B.原点 O 的坐标是 0
C.原点 O 既在 X 轴上也在 Y 轴上 D.原点 O 在坐标平面内
8.X 轴上的点 P 到 Y 轴的距离为 2.5,则点P的坐标为( )
A.(2.5,0) B.(-2.5,0) C.(0,2.5) D.(2.5,0)或(-2.5,0)
9.三角形 ABC 三个顶点的坐标分别是 A(4,3)B(3,1)C(1,2),请你在平面直角坐标系中描出这个三角形,
然后先将其向左平移 4 个单位,再将其向下平移 2 个单位,画出平移后的图形并写出相应顶点的坐标。
10.如图,写出三角形 ABC 各顶点的坐标并且求出三角形的面积。
二次备课
课后反思
第 20 课时 第六章平面直角坐标系 单元测试
(x-a,y)
(x,y+b)
(x,y-b)
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
39
班级: 姓名: 学号: 得分:
【学习目标】
1.了解平面直角坐标系中的各象限及各象限的点的坐标的符号的特点。(坐标轴上的点不属于任何象限)
2.根据点的坐标,确定点的位置。
3.建立平面直角坐标系,确定图形的点的坐标。
4.认识平面直角坐标系,了解点的坐标的意义;
5.会用坐标表示点,能画出点的坐标位置.
6.掌握坐标变化与图形平移的关系,能利用点的平移规律将图形进行平移;
【学习重点】平面直角坐标系的概念和点的坐标的确定. 掌握坐标变化与图形平移的关系.
【学习难点】正确画平面直角坐标系,并能找到对应点. 利用坐标变化与图形平移的关系解决实际问题.
一、选择题(本大题共 10 题,每小题 3 分,共 30 分,每小题只有一个正确选项,把正确选项的代号填
在题后的括号里)
1.根据下列表述,能确定位置的是( )
A.红星电影院 2 排 B.北京市四环路 C.北偏东 30° D.东经 118°,北纬 40°
2.若点 A(m,n)在第三象限,则点 B(|m|,n)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3.若点 P 在 x 轴的下方,y 轴的左方,到每条坐标轴的距离都是 3,则点 P 的坐标为( )
A.(3,3) B.(−3,3) C.(−3,−3) D.(3,−3)
4.点 P(x,y),且 xy<0,则点 P 在( )
A.第一象限或第二象限 B.第一象限或第三象限
C.第一象限或第四象限 D.第二象限或第四象限
5.如图,与图(1)中的三角形相比,图(2)中的三角形发生的变化是( )
A.向左平移 3 个单位长度 B.向左平移 1 个单位长 度
C.向上平移 3 个单位长度 D.向下平移 1 个单位长度
6.如图所示,若在象棋盘上建立直角坐标系,使“将”位于点(1,−2),“象”位于点(3,−2),则“炮”
位于点( )
A.(1,−1) B.(−1,1)
C.(−1,2) D.(1,−2)
7.若点 M(x,y)的坐标满足 x+y=0,则点 M 位 于( )
A.第二象限 B.第一、三象限的夹角平分线上 C.第四象限 D.第二、四象限的夹角平分线上
8.将△ABC 的三个顶点的横坐标都加上−1,纵坐标不变,则所得图形与原图形的关系是( )
A.将原图形向 x 轴的正方向平移了 1 个单位 B.将原图形向 x 轴的负方向平移了 1 个单位
C.将原图形向 y 轴的正方向平移了 1 个单位 D.将原图形向 y 轴的负方向平移了 1 个单位
9.在坐标系中,已知 A(2,0),B(−3,−4),C(0,0),则△ABC 的面积为( )
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
40
A.4 B. 6 C.8 D.3
10.点 P(x−1,x+1)不可能在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
二、填空题(本大题共 6 小题,每小题 3 分,共 18 分)
11.已知点 A 在 x 轴上方,到 x 轴的距离是 3,到 y 轴的距离是 4,那么点 A 的坐标是______________.
12.已知点 A(−1,b+2)在坐标轴上,则 b=________.
13.如果点 M(a+b,ab)在第二象限,那么点 N(a,b)在第________象限.
14.已知点 P(x,y)在第四象限,且|x|=3,|y|=5,则点 P 的坐标是______.
15.已知点 A(−4,a),B(−2,b)都在第三象限的角平分线上,则 a+b+ab 的值等于________.
16.已知矩形 ABCD 在平面直角坐标系中的位置如图所示,将矩形 ABCD 沿 x 轴向左平移到使点 C 与坐标原点
重合后,再沿 y 轴向下平移到使点 D 与坐标原点重合,此时点 B 的坐标是________.
三、(本大题共 3 小题,每题 5 分,共 15 分)
17.如图,正方形 ABCD 的边长为 3,以顶点 A 为原点,且有一组邻边与坐标轴重合,求出正方形 ABCD 各个
顶点的坐标.
18.若点 P(x,y)的坐标 x,y 满足 xy=0,试判定点 P 在坐标平面上的位置.
19.已知,如图在平面直角坐标系中,S△ABC=24,OA=OB,BC=12,求△ABC 三个顶点的坐标.
四、(本大题共 3 小题,每题 6 分,共 18 分)
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
41
20.在平面直角坐标系中描出下列各点 A(5,1),B(5,0),C(2,1),D(2,3),并顺次连接,且
将所得图形向下平移 4 个单位,写出对应点 A'、B'、C'、D'的坐标.
21.已知三角形的三个顶点都在以下表格的交点上,其中 A(3,3),B(3,5),请在表格中确立 C 点的位
置,使 S△ABC=2,这样的点 C 有多少个,请分别表示出来.
22.如图,点 A 用(3,3)表示,点 B 用(7,5)表示,若用(3,3)→(5,3)→(5,4)→(7,4)→(7,
5)表示由 A 到 B 的一种走法,并规定从 A 到 B 只能向上或向右走,用上述表示法写出另两种走法,并判断这几
种走法的路程是否相等.
五、(本大题共 2 小题,第 23 题 8 分,第 24 题 11 分,共 19 分)
23.(8 分)如下图所示,在直角坐标系中,第一次将△OAB 变换成△OA1B1,第二次将△OA1B1 变换成△OA2B2,
第三次将△OA2B2 变换成△OA3B3,已知 A(1,3),A1(2,3), A2(4,3),A3(8,3),B(2,0),B1(4,0),B2(8,0),
B3(16,0).
(1)观察每次变换前后的三角形有何变化,找出规律,按此变换规律将△OA4B4 变换成△OA5B5,则 A5 的坐标是
_________,B5 的坐标是_________.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
42
(2)若按第(1)题的规律将△OAB 进行了 n 次变换,得到△OAnBn,比较每次变换中三角形顶点坐标有何变化,
找出规律,请推测 An 的坐标是_________,Bn 的坐标是_________.
24.如图,△ABC 在直角坐标系中,
(1)请写出△ABC 各点的坐标;
(2)求出 S△ABC ;
(3)若把△ABC 向上平移 2 个单位,再向右平移 2 个单位得△A′B′C′,在图中画出△ABC 变化位置,并写
出 A′、B′、C′的坐标.
二次备课
课后反思
第 21 课时:7.1.1 三角形的边导学案 班级 姓名
【学习目标】1.认识三角形,能用符号语言表示三角形,并把三角形分类.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
43
2.知道三角形三边不等的关系.
3.懂得判断三条线段能否构成一个三角形的方法,并能用于解决有关的问题
【学习重点】知道三角形三边不等关系.
【学习难点】 判断三条线段能否构成一个三角形的方法.
【学习过程】
一、学前准备
回忆你所学过或知道的三角形的有关知识。并写出来。
二、探索思考
知识点一:三角形概念及分类
1、学生自学课本 63-64 页探究之前内容,并完成下列问题:
(1)三角形概念:由不在同一直线上的三条线段___________________所组成的图形叫做三角形。
如图,线段____、______、______是三角形的边;点 A、B、C 是三角形的______; _____、 ______、_______
是相邻两边组成的角,叫做三角形的内角,简称三角形的角。图中三角形记作__________。
(2)三角形按角分类可分为_____________、______________、_________________。
(3)三角形按边分类可分为 _____________
三角形 _____________
——————— _____________
(4)如图 1,等腰三角形 ABC 中,AB=AC,腰是__________,
底是_________,顶角指_______,底角指_____________.
等边三角形 DEF 是特殊的_______三角形,DE=____=_____.
练习一: 图 1
1、如图 2.下列图形中是三角形的有_______________?
图 2
2、图 3 中有几个三角形?用符号表示这些三角形.
A
B C
D
E F
A
B C
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
44
知识点二:知道三角形三边的不等关系,并判断三条线段能否构成三角形
1、探究:请同学们画一个△ABC,分别量出 AB,BC,AC 的长,并比较下列各式的大小:
AB+BC_____AC AB+ AC _____ BC AC +BC _____ AB
从中你可以得出结论:__________________________________________。
练习二:
1、下列长度的三条线段能否组成三角形?为什么?
(1)3,4,8; (2)5,6,11; (3)5,6,10
2、有四根木条,长度分别是 12cm、10cm、8cm、4cm,选其中三根组成三角形,能组成三角形的个数是_______
个。
(3)如果三角形的两边长分别是 3 和 5,那么第三边长可能是( )
A、1 B、9 C、3 D、10
3、阅读课本 64 页例题,仿照例题解法完成下面这个问题:
一个三角形有两条边相等,周长为 20cm,三角形的一边长 6cm,求其他两边长。
三、当堂反馈
1、 课本 69 页 1、2 题
2、 一个等腰三角形的两边长分别是 2 和 5,则它的周长是( )
A、7 B、9 C、12 D、9 或 12
3、若三角形的周长是 60cm,且三条边的比为 3:4:5,则三边长分别为___________.
4、(选做)若△ABC 的三边长都是整数,周长为 11,且有一边长为 4,则这个三角形可能的最大边长是___________.
5、(选做)已知线段 3cm,5cm,xcm,x 为偶数,以 3,5,x 为边能组成______个三角形。
四、课堂小结:本节课你学到了那些知识?
五、课后反思
第 22 课时:7.1.2 三角形的高,中线,角平分线导学案 班级 姓名
【学习目标】1.认识并会画出三角形的高线,利用其解决相关问题;
2.认识并会画出三角形的中线,利用其解决相关问题;
3.认识并会画出三角形的角平分线,利用其解决相关问题;
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
45
【学习重点】 认识三角形的高线、中线与角平分线,并会画出图形
【学习难点】 画出三角形的高线、中线与角平分线.
【学习过程】
一、学前准备
1、三角形按边分可分为什么?按角分可分为什么?
2、下列长度的三个线段能否组成三角形?
(1)3,6,8 (2)1,2,3 (3)6,8,2
二、探索思考
知识点一:认识并会画三角形的高线,利用其解决相关问题
自学课本 65 页三角形的高并完成下列各题:
1、作出下列三角形三边上的高:
2、上面第 1 图中,AD 是△ABC 的边 BC 上的高,则∠ADC=∠ = °
3、由作图可得出如下结论:(1)三角形的三条高线所在的直线相交于 点;(2)锐角三角形的三条高相交于三
角形的 ;(3)钝角三角形的三条高所在直线相交于三角形的 ;(4)直角三角形的三条高相交三
角形的 ;(5)交点我们叫做三角形的垂心。
练习一:如图所示,画△ABC 的一边上的高,下列画法正确的是( ).
知识点二:认识并会画三角形的中线,利用其解决相关问题
自学课本 65 页三角形的中线并完成下列各题:
1、 作出下列三角形三边上的中线
2、AD 是△ABC 的边 BC 上的中线,则有 BD = =
2
1 ,
3、由作图可得出如下结论:(1)三角形的三条中线相交于 点;(2)锐角三 角 形 的 三
条中线相交于三角形的 ;(3)钝角三角形的三条中线相交于三角形 的 ;
(4)直角三角形的三条中线相交于三角形的 ;(5)交点我们叫做三角形 的重心。
练习二:如图,D、E 是边 AC 的三等分点,图中有 个三角形,BD 是三角 形
中 边上的中线,BE 是三角形 中________上的中线;
知识点三:认识并会画三角形的角平分线,利用其解决相关问题
自学课本 66 页三角形的角平分线并完成下列各题:
1、作出下列三角形三角的角平分线:
A
CB
A
CB
A
CB
A
CB
A
CB
A
CB
教师备课札记
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
46
2、AD 是△ABC 中∠BAC 的角平分线,则∠BAD=∠ =
3、由作图可得出如下结论:(1)三角形的三条角平分线相交于 点;(2)锐角三角形的三条角平分线相交三角
形的 ;(3)钝角三角形的三条角平分线相交三角形的 ;(4)直角三角形的三条角平分线相交三角形
的 ;(5)交点我们叫做三角形的内心。
练习三:如图,已知∠1=
2
1 ∠BAC,∠2 =∠3,则∠BAC 的平分线为 , ∠ ABC 的 平
分线为 .
总结:三角形的高、中线、角平分线都是一条线段。
三、当堂反馈
1.课本 69 页第 4 题。
2.三角形的角平分线是( ).
A.直线 B.射线 C.线段 D.以上都不对
3.下列说法:①三角形的角平分线、中线、高线都是线段;②直角三角形只有一条高线;③三角形的中线可能
在三角形的外部;④三角形的高线都在三角形的内部,并且相交于一点,其中说法正确的有( ).
A.1 个 B.2 个 C.3 个 D.4 个
4.如图,AD 是△ABC 的高,AE 是△ABC 的角平分线,AF 是△ABC 的中线,写出图中所有相等的角和相等的线段。
5.(选做)在△ABC 中,AB=AC,AC 边上的中线 BD 把三角形的周长
分为 12cm 和 15cm 两部分,求三角形各边的长.
6.(选做)课本 70 页第 8 题
四、课堂小结 本节课你学到了那些知识?
五、课后反思
第 23 课时:7.1.3 三角形的稳定性导学案 班级 姓名
【学习目标】1.认识三角形的稳定性,并会用其解决一些实际问题;
2、通过练习进一步巩固三角形的边和相关线段。
【学习重点】三角形的稳定性
【学习难点】三角形的稳定性的理解
【学习过程】
一、学前准备 找找生活中的引用三角形和四边形的例子,写出来。
二、探索思考
知识点一:三角形的稳定性
A
CB DEF
A
B C
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
47
自学课本 67-68 页内容,回答下列问题:
1、通过观察,你发现生活中哪些物体的结构是三角形?
二、做一做
1、用三根木条用钉子钉成一个三角形木架,然后扭动它,它的形状会改变吗?
2、用四根木条用钉子钉成一个四边形木架,然后扭动它,它的形状会改变吗?
3、在四边形的木架上再钉一根木条,将它的一对顶点连接起来,然后扭动它,它的形状会改变吗?
4、如图 4 所示,盖房子时,在窗框未安装好之前,木工师傅常常先在窗框上斜钉一根木条,为什么要这样做呢?
6、想一想:在实际生活中还有哪些地方利用了“三角形的稳定性”来为我们服务?“四边形易变形”是优点还
是缺点?生活中又有哪些应用?
练习
1. 如图,木工师傅做完门框后,为了防止变形,常常像图中所示那样钉上两条斜拉的木条,这样做的数学道理
是 ;
2.⑴ 下列图中哪些具有稳定性? 。
1 2 3 4 5 6
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
48
⑵ 对不具稳定性的图形,请适当地添加线段,使之具有稳定性。
3、造房子的屋顶常用三角结构,从数学角度来看,是应用了______________,而活动接架则应用了四边形的
_______________。
知识点二:通过练习进一步巩固三角形的边和相关线段
三、当堂反馈
1.如图:(1)在△ABC 中,BC 边上的高是________
(2)在△AEC 中,AE 边上的高是________
(3)在△FEC 中,EC 边上的高是_________
(4)若 AB=CD=2cm,AE=3cm,则 = _______,CE=_______。
2.以下列各组线段长为边,能组成三角形的是 ( )
A.1cm,2cm,4cm; B.8cm,6cm,4cm C.12cm,5cm,6cm; D.2cm,3cm,6cm
3.已知等腰三角形的两边长分别为 6cm 和 3cm,则该等腰三角形的周长是( )
A.9cm B. 12cm C. 12cm 或 15cm D. 15cm
4.如图,为估计池塘岸边 A、B 的距离,小方在池塘的一侧选取
一点 O,测得 OA=15 米,OB=10 米,A、B 间的距离
不可能是( )
A.20 米 B.15 米 C.10 米 D.5 米
5、如图,点 D 是 BC 边上的中点,如果 AB=3 厘米,AC=4 厘米,
则△ABD 和△ACD 的周长之差为________,面积之差为__________。
四、课堂小结 本节课你学到了那些知识?
五、课后反思
第 24 课时:与三角形有关的线段练习导学案 班级 姓名
【学习目标】通过练习进一步巩固三角形的边和相关线段。
【学习重点】巩固三角形的边和相关线段;
【学习难点】 三角形三边不等关系的运用
【学习过程】
一、学前准备
1、什么叫做三角形?
2、三角形按边可分为什么?按角可分为什么?
3、三角形三边不等关系是什么?
A
O
B
A
B D
C
AEC
s △
_F_A
_D
_C
_B
_E
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
49
4、三角形的高、中线、角平分线各有什么特征?
5、三角形具有_______性,四边形具有_________性。
二、达标检测:
1.如图 1,图中所有三角形的个数为 ,在△ABE 中,AE 所对的角是 ,∠ABC 所对的边是 ,在△ADE
中,AD 是∠ 的对边,在△ADC 中,AD 是∠ 的对边;
2.如图 2,已知∠1=
2
1 ∠BAC,∠2 =∠3,则∠BAC 的平分线为 ,∠ABC 的平分线为 ;
3.如图 3,D、E 是边 AC 的三等分点,图中有 个三角形,BD 是三角形 中 边上的中线,BE 是
三角形 中 边上的中线;
图 1 图 2 图 3
4.若等腰三角形的两边长分别为 7 和 8,则其周长为 ;若两边长分别为 4 和 8,则其周长为_____.
5. 如右图,木工师傅做完门框后,为了防止变形,常常像图中所示
那样钉上两条斜拉的木条(图中的 AB、CD),
这样做的数学道理是 ;
6. 一个三角形的三边之比为 2∶3∶4,周长为 36cm,则此三角形三边的长分别为_____________.
7.已知△ABC 中,AD 为 BC 边上的中线,AB=10cm,AC=6cm,则△ABD 与△ACD 的周长之差为________.
7.如右图,图中共有三角形 ( )
A、4 个 B、5 个 C、6 个 D、8 个
8.下列长度的三条线段中,能组成三角形的是 ( )
A、 3cm,5cm ,8cm B、8cm,8cm,18cm
C、0.1cm,0.1cm,0.1cm D、3cm,40cm,8cm
9.如果线段 a,b,c 能组成三角形,那么,它们的长度比可能是 ( )
A、1∶2∶4 B、1∶3∶4 C、3∶4∶7 D、2∶3∶4
10.如果三角形的两边分别为 7 和 2,且它的周长为偶数,那么第三边的长为 ( )
A、5 B、6 C、7 D、8
11.如图,分别画出三角形过顶点 A 的中线、角平分线和高。
A
BC C CB B
AA
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
50
12.已知:△ABC 的周长为 48cm,最大边与最小边之差为 14cm,另一边与最小边之和为 25cm,求:△ABC 的各边
的长。
13.⑴ 已知等腰三角形的一边等于 8cm,另一边等于 6cm,求此三角形的周长;
⑵ 已知等腰三角形的一边等于 5cm,另一边等于 2cm,求此三角形的周长。
14.在△ABC 中 AB=AC,AC 上的中线 BD 把三角形的周长分为 24cm 和 30cm 的两个部分,求三角形的三边长。
15.【探究】如图,在△ABC 中,若 AD 是 BC 边上的中线,则有 BD = =
2
1 ,若过 A 点作 BC 边上的高 AE,
利用三角形的面积公式可求得 S△ABD= =
2
1 S△ABC,
请你任意画一个三角形,将这个三角形的面积四等分。
三、课后反思
第 25 课时:7.2.1 三角形的内角导学案 班级 姓名
【学习目标】1.经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2.能应用三角形内角和定理解决一些简单的实际问题
【学习重点】三角形内角和定理
【学习难点】三角形内角和定理的推理的过程
【学习过程】
一、学前准备
每个学生准备好二个由硬纸片剪出的三角形
二、探索思考
知识点一:探究三角形的内角和定理
A
CB D E
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
51
1、自学课本 72-73 页内容,利用手中的硬纸片运用拼合法探究三角形的内角和。
(1)在所准备的三角形硬纸片上标出三个内角的编码
(2)叫几名同学到黑板运用不同的方法粘贴演示。
(3)由拼合过程你能想出证明三角形内角和等于 180°的方法吗?
2、证明三角形的内角和定理
(1)阅读课本 73 页证明过程。
(2)仿照课本证明过程选择下面的任意一个图形中辅助线的做法,完成证明。
图一 图二
3、 归纳:(1)三角形的内角和等于 180°。
(2)证明是由题设(已知)出发,经过一步步的推理,最后推出结论(求证)正确的过程。
知识点二:应用三角形内角和定理解决简单的实际问题
练习
1、填空: (1)在△ABC 中,∠A = 60°∠B = 30°,则∠C = ;
(2)三角形的三个内角之比为 1∶3∶5,那么这个三角形的最大内角为 ;
(3)在△ABC 中,∠A =∠B = 4∠C,则∠C = ;
(4)在△ABC 中,∠A = 40°,∠B =∠C,则∠B = ;
2、例:如图,C 岛在 A 岛的北偏东 50 方向,B 岛在 A 岛的北偏东 80 方向,C 岛在 B 岛的北偏西 40 方向,从
C 岛看 A、B 两岛的视角 ACB 是多少度?
A
B C D
E
A
B C
E
教
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
52
三、当堂反馈
1、判断:
(1) 三角形中最大的角是 70 ,那么这个三角形是锐角三角形( )
(2) 一个三角形中最多只有一个钝角或直角( )
(3)一个等腰三角形一定是锐角三角形( )
(4) 一个三角形最少有一个角不大于 60 ( )
2、课本 76 页习题 7.1 第 1、2 题
3、课本 74 页练习 1、2
四、课堂小结本节课你学到了什么?
五、课后反思
第 26 课时:7.2.2 三角形的外角导学案 班级 姓名
【学习目标】1.认识三角形的外角;
2.知道三角形的外角的两个性质;
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
53
3.能利用三角形的外角性质解决实际问题。
【学习重点】三角形外角的两个性质;
【学习难点】三角形的外角性质的证明
【学习过程】
一、学前准备
1. 三角形的内角和是多少?
2.△ABC 中,∠A=50°,∠B=60°,则∠C=________.
3.△ABC 中,∠A:∠B:∠C=1:2:2,则∠A=_____,∠B=______,∠C=_______.
二、探索思考
知识点一:三角形外角的定义
1、自学课本 74 页第一段理解三角形的外角的定义。
2、任意画一个三角形,并画出三角形的外角。像这样,三角形的一边与_______________组成的角,叫做三角形
的外角。
3、找出右图中的外角 。
4、一个三角形有几个外角? 。
知识点二:三角形外角的两个性质
1、探究外角的性质
(1)如图 9,△ABC 中,∠A=70°,∠B=60°.∠ACD 是△ABC 的一个外角.能由∠A,∠B 求出∠ACD 吗?如果
能,∠ACD 与∠A,∠B 有什么关系?
(2)你能进一步说明任意一个三角形的一个外角与它不相邻的两个内 角 有 什 么
关系呢?并说明理由?
结论:________________________________________
理由:
(3)外角与其中一个不相邻的内角之间的关系呢?
结论:_________________________________________
理由
练习
(1) 课本 75 页练习
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
54
(2)在△ABC 中,∠B=50°,∠C 的外角等于 100°,则∠A=_____.
(3) 如右图所示,则∠a=________.
3、自学课本 75 页例 2 从中你会发现什么结论?
结论:_____________________________________.
三、当堂反馈
1.若三角形的外角中有一个是锐角,则这个三角形是________三角形.
2.△ABC 中,若∠C-∠B=∠A,则△ABC 的外角中最小的角是______(填“锐角”、“直角”或“钝角”).
3.如图 1,x=______.
(1) (2) (3)
4.如图 2,△ABC 中,点 D 在 BC 的延长线上,点 F 是 AB 边上一点,延长 CA 到 E,连 EF,则∠1,∠2,∠3 的
大小关系是_________.
5.如图 3,在△ABC 中,AE 是角平分线,且∠B=52°,∠C=78°,求∠AEB 的度数
6.如图所示,AE∥BD,∠1=95°,∠2=28°,求∠C
四、课堂小结 通过本节课学习,你有什么收获?
五、课后反思
第 27 课时:7.3.1 多边形导学案 班级 姓名
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
55
【学习目标】
1.知道多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念.
2.能够解决与多边形的对角线有关的问题
【学习重点】多边形的相关概念;
【学习难点】多边形对角线
【学习过程】
一、学前准备
知识点一:多边形、多边形的内角、多边形的外角、多边形的对角线和正多边形的有关概念
二、探索思考
1、自学课本 79-----80 页,完成下列问题:
(1)在平面内,由一些线段________________相接组成的 ________叫
做多边形。图 1 中分别是什么多边形?
(2)多边形_________组成的角叫做多边形的内角。图 2 中 内角有
____________________。
(3)多边形的边与它的的邻边的__________组成的角叫做
多边形的外角。图 2 中外角有______________________。
(4)连接多边形_________的两个顶点的线段叫做多边形的对角线。
(5)_________都相等,_________都相等的多边形叫做正多边形。
2、对应练习(1)n 边形有_______条边,______个顶点,________个内角。
(2)图 3 是_________边形,它的边是___________________,顶点是_______________,内角是________________,
若图中多边形是正多边形,则_______________________________________。
(3)下列图形不是凸多边形的是( ).
知识点二:解决与多边形的对角线有关的问题
1 、 探究:画出下列多边形的对角
线.回答问题:
(1)从四边形的一个顶点出
发可以画_____条对角线,把四边形分成了 个三角形;四边形共有____条对角线.
(2)从五边形的一个顶点出发可以画_____条对角线,把五边形分成了 个三角形;五边形共有____条对角线.
(3)从六边形的一个顶点出发可以画_____条对角线,把六边形分成了 个三角形;六边形共有____条对角线.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
56
(4)猜想:①从 100 边形的一个顶点出发可以画_____条对角线,把 100 边形分成了 个三角形;
100 边形共有___条对角线.②从 n 边形的一个顶点出发可以画_____条对角线,把 n 分成了 个三角形;
n 边形共有_____条对角线.
练习:
(1)从 n 边形的一个顶点出发可作______条对角线,从 n边形 n个顶点出发可作_____条对角线,除去重复
作的对角线,则 n 边形的对角线的总数为_____条.
(2)过 m 边形的一个顶点有 7 条对角线,n 边形没有对角线,k 边形有 2 条对角线,则(m-k)=________.
(3)过十边形的一个顶点可作出几条对角线?把十边形分成了几个三角形?
(4)十二边形共有 条对角线,过一个顶点可作 条对角线,可把十二边形分成 个三角形。
三、当堂反馈
1、课本 81 页练习
2、下列图形中,是正多边形的是( )A.直角三角形 B.等腰三角形 C.长方形 D.正方形
3、九边形的对角线有( ) A.25 条 B.31 条 C.27 条 D.30 条
4、 过 n 边形的一个顶点的所有对角线,把多边形分成 8 个三角形,则这个多边形的边数是_______。
5、 一个多边形的对角线的条数等于它的边数的 4 倍,求这个多边形的边数 。
6、 6、1 如图, 3,2,1 是三角形 ABC 的不同三个外角,则 321
7、2 三角形的三个外角中最多有 锐角,最多有 个钝角,最多有 个直角
8、3 ABC 的两个内角的一平分线交于点 E, 52A ,则 BEC
9、4 已知 ABC 的 CB , 的外角平分线交于点 D, 40A ,那么 D =
10、5 如图, BDC 是 外角, BDC + , EFC 是 外角, EFC = + ,
BFC 是 外角, BFC = + , BFC > , BFC >
11、6 在 ABC 中 A 等于和它相邻的外角的四分之一,这个外角等于 B 的两倍,那么
A , B , C
四、课堂小结 通过本节课学习,你有什么收获?
五、课后反思
第 28 课时:7.3.2 多边形的内角和导学案 班级 姓名
【学习目标】 1.知道多边形的内角和与外角和定理;
2.运用多边形内角和与外角和定理进行有关的计算.
【学习重点】多边形的内角和与外角和定理;
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
57
【学习难点】内角和定理的推导
【学习过程】
一、学前准备
1.三角形的内角和是多少? 。
2.正方形、长方形的内角和是多少?
3.从 n 边形的一个顶点出发可以画_____条对角线,把 n 边形分成了 个三角形;
二、探索思考
知识点一:多边形的内角和定理
探究 1:任意画一个四边形,量出它的 4 个内角,计算它们的和.再画几个四边形,量一量、算一算.你能得
出什么结论? 能否利用三角形内角和等于 180°得出这个结论?
结论: 。
探究 2:从上面的问题,你能想出五边形和六边形的内角和 各 是 多 少
吗?观察图 3,请填空:
(1)从五边形的一个顶点出发,可以引_____条对角 线,它们将
五边形分为_____个三角形,五边形的内角和等于 180°× ______.
(2)从六边形的一个顶点出发,可以引_____条对角 线,它们将
六边形分为_____个三角形,六边形的内角和等于 180°×______.
探究 3:一般地,怎样求 n 边形的内角和呢?请填空:
从 n 边形的一个顶点出发,可以引____条对角线,它们将 n 边形分为____个三角形,n 边形的内角和等于 180°
×______.
结论:多边形的内角和与边数的关系是 。
练习一
1.十二边形的内角和是_________.
2.一个多边形的内角和等于 900°,求它的边数.
3.课本 83 页练习。
知识点二:多边形的外角和
探究 4:如图 8,在六边形的每个顶点处各取一个外角,这些外角的和叫做六边形的外角和.六边形的外角和等
于多少?
问题:如果将六边形换为 n 边形(n 是大于等于 3 的整数),结果还相同吗?
因此可得结论: .
练习二
1、 七边形的外角和是_________;十二边形的外角和是____________;三角形的外角和是_______。
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
58
2、 一个多边形的每一个外角都等于 36°则这个多边形是_______边形。
3、 在每个内角都相等的多边形中,若一个外角是它相邻内角的
2
1 ,则这个多边形是______边形。
三、当堂反馈
1、一个多边形的每一个外角都等于 40°,则它的边数是__________;一个多边形的每一个内角都等于 140°,
则它的边数是___________。
2、如果四边形有一个角是直角,另外三个角的度数之比为 2:3:4,那么这三个内角的度数分别为________。
3、若一个多边形的内角和为 1080°,则它的边数是___________。
4、当一个多边形的边数增加 1 时,它的内角和增加_________度。
3、 正十边形的一个外角为______.
4、_______边形的内角和与外角和相等.
5、已知一个多边形的内角和与外角和的差为 1080°,则这个多边形是_____边形.
6、若一个多边形的内角和与外角和的比为 7:2,求这个多边形的边数。
四、课堂小结 通过本节课学习,你有什么收获?
五、课后反思
第 29 课时:7.4 镶嵌导学案 班级 姓名
【学习目标】1.知道平面图形的镶嵌,弄清多边形镶嵌的条件.
2.通过探究多边形镶嵌的过程,发展学生的动手能力,合情推理能力,合作能力等.
【学习重点】平面图形的镶嵌
【学习难点】多边形镶嵌的条件
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
59
【学习过程】
一、学前准备
1、多边形的内角和怎样计算?2、多边形的外角和是多少度?
二、探索思考
知识点一:镶嵌定义
用形状、大小完全相同的一种或几种平面图形进行拼接,彼此之间不留空隙、不重叠地铺成一片,这就是平面图
形的密铺,又称平面图形的镶嵌
知识点二:一种正多边形的平面镶嵌
活动 1.问题:分别剪一些边长相同的正三角形、正方形、正五边形、正六边形,如果用其中一种正多边形镶嵌,
哪几种正多边形能镶嵌成一个平面图案?
结论:
问题 2:观察每个拼接点处有几个角?它们与正多边形的每个内角有什么关系?它们的和又有何特征?用简洁的
语言总结出规律:
练习:
1.用多边形把平面的一部分完全覆盖的意思是指既不留下______,又不_____,这与多边形的_______有关.
2.下列图形不能用来铺满地面的是( ).
A.钝角三角形 B.长方形 C.梯形 D.正五边形
3.下列说法正确的是( ).
A.只有正多边形可以平面镶嵌; B.最多能用两种正多边形进行平面镶嵌
C.一般的凸多边形也可以平面镶嵌; D.只有正五边形不可以平面镶嵌
4.我们已经知道,用一种正多边形铺地面时,只有______,_______,_______三种能铺满地面。
知识点三:两种正多边形的平面镶嵌
活动 2.问题: 用刚才剪出的边长相同的正三角形、正方形、正五边形、正六边形中的两种正多边形镶嵌,哪
两种正多边形能镶嵌成一个平面图案?
由此可得出结论:
练习:
1.有以下边长相等的三种图形:①正三角形;②正方形;③正八边形.选其中两种图形镶嵌成平面图形,请你
写出两种不同的选法:_______或________.(用序号表示图形)
2.当围绕一个顶点拼在一起的多边形中有_____个正三角形与______个正方形,这个组合能铺满平台;当围绕一
个顶点拼在一起的多边形中有______个正三角形与_______个正方形和______个正六边形,则这个组合也能平
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
60
面镶嵌.
3.不能铺满地面的正多边形的组合是( ).
A.正三角形和正五边形 B.正方形和正八边形
C.正三角形和正十二边形 D.正三角形,正方形和正六边形
知识点四:任意相同三角形或四边形的平面镶嵌
活动 3.问题:任意剪出一些形状、大小相同的三角形纸板,拼拼看,它们能否镶嵌成平面图案.
任意剪出一些形状、大小相同的四边形纸板,拼拼看,它们能否镶嵌成平面图案.
总结:用一些形状、大小相同的多边形,它们能够镶嵌成平面图案的条件是什么?
结论: .
三、当堂反馈
1.用多边形或其组合可以拼成许多漂亮的密铺图案.下面的图案是现实生活中大量存在的密铺图案的一部
分.欣赏这些图案,你能发现哪些多边形或其组合可以密铺?
2.同学们经常见到如图所示那样的地面,它们分别是全用正方形或全用正六边形材料铺成的,这样形状的材料能
铺成平整、无空隙的地面.现在,问:
(1)像上面那样铺地面,能否全用正五边形的材料?
(2)你能不能另外想出一个用一种多边形(不 一定是正多边
形)
的材料铺地的方案?把你想到的方案画成草图.
(3)请你再画一个用两种不同的正多边形材料铺地的草图.
四、课堂小结
五、课后反思
第 30 课时: 三角形复习题导学案 班级 姓名
【学习目标】通过做练习进一步巩固三角形的基本知识点
【学习重点】三角形的边角关系,特殊的三角形和多边形
【学习难点】所学知识的综合引用
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
61
A
B
CE A
B
C E
A
B
C
E
A
B
C
E
A B C D
1.如图 1 所示,共有_____个三角形,其中以 AB 为边的三角形有_____,以∠C为一个内角的三角形有______.
2.以下面各组线段为边,能组成三角形的是( ).
A.1cm,2cm,4cm B.8cm,6cm,4cm
C.12cm,5cm,6cm D.2cm,3cm,6cm
3.D 是△ABC 内一点,那么,在下列结论中错误的是( ).
A . BD+CD>BC B . ∠ BDC> ∠ A C . BD>CD D.AB+AC>BD+CD
4.等腰三角形的周长为 20cm,一边长为 6cm,则底边长为______.
5.下列图形中有稳定性的是( )
A.正方形 B.长方形 C.直角三角形 D.平行四边形
6.下列四组图形中,BE 是△ABC 的高线的图是( )
7.下列说法中正确的是 ( )
A.三角形的内角中至少有两个锐角 B.三角形的内角中至少有两个钝角
C.三角形的内角中至少有一个直角 D.三角形的内角中至少有一个钝角
8.已知在△ABC 中,∠A=40°,∠B-∠C=40°,则∠B=_____,∠C=______.
9.如图 2 所示,∠α=_______.
10.一个三角形的两个内角分别是 55°和 65°,这个三角形的外角不可能是( ).
A.115° B.120° C.125° D.130°
11.三角形的三个外角中,钝角的个数最多有______个,锐角最多_____个.
12.在△ABC 中,∠A =60°,∠C =2∠B,则∠C =__________.
13.正多边形的一个内角等于 144°,则该多边形是正( )边形.
A.8 B.9 C.10 D.11
14.若 n 边形的内角和是 1260°,则边数 n 为( ).
A.8 B.9 C.10 D.11
15.某人到瓷砖店去购买一种多边形形状的瓷砖,用来铺设无缝地板,他购买的瓷砖形状不可以是
( ). A.正三角形 B.矩形(长方形) C.正八边形 D.正六边形
16.如图,BD 平分∠ABC,DA⊥AB,∠1=60°,∠BDC=80°,求∠C 的度数.
17.如图:(1)画△ABC 的外角∠BCD,再画∠BCD 的平分线 CE.
(2)若∠A=∠B,请完成下面的证明:
已知:△ABC 中,∠A=∠B,CE 是外角∠BCD 的平分线.
求证:CE∥AB.
图 1
图 2
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
62
18.一个多边形的内角和是它的外角和的 4 倍,求这个多边形的边数.
19.一个零件的形状如图,按规定∠A= 90°,∠ABC 和∠ACB,应分别是 32°和 21°,检验工人量得∠BDC = 148°,
就断定这个零件不合格,运用三角形的有关知识说明零件不合格的理由
20.如图所示,有一块三角形 ABC 空地,要在这块空地上种植草皮来美化环境,已知这种草皮每平方米售价 230
元,AC=12m,BD=15m,购买这种草皮至少需要多少元?
21.如图所示,在△ABC 中:(1)画出 BC 边上的高 AD 和中线 AE.
(2)若∠B=30°,∠ACB=130°,求∠BAD 和∠CAD 的度数.
22.在△ABC 中,已知∠ABC = 66°∠ACB = 54°,BE 是 AC 上的高,CF 是 AB 上的高,H 是 BE 和 CF 的交点,求
∠BHC 的度数。
课后反思
第 31 课时:三角形单元测试导学案 班级 姓名
一、选择题(3 分×8=24 分)
1.一个三角形的三个内角中 ( )
A 、至少有一个钝角 B 、至少有一个直角
C 、至多有一个锐角 D、 至少有两个锐角
2. 下列长度的三条线段能组成三角形的是 ( )
A、 3,4,8 B、 5,6,11 C、 1,2,3 D、 5,6,10
3.关于三角形的边的叙述正确的是 ( )
A、 三边互不相等 B、 至少有两边相等
A
B
C
D
D A
B C
15m 12m
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
63
C、 任意两边之和一定大于第三边 D、 最多有两边相等
4.图中有三角形的个数为 ( )
A、 4 个 B、 6 个 C、 8 个 D、 10 个
5. 如图在△ABC 中,∠ACB=900,CD 是边 AB 上的高。那么图中与∠A 相等的角
是 ( )
A、 ∠B B、 ∠ACD C、 ∠BCD D、 ∠BDC
6.下列图形中具有稳定性有 ( )
A、 2 个 B、 3 个 C、 4 个 D、 5 个
7.一个多边形的内角和等于它的外角和,这个多边形是 ( )
A 、三角形 B、 四边形 C、 五边形 D、 六边形
8.一个多边形内角和是 10800,则这个多边形的边数为 ( )
A、 6 B、 7 C、 8 D、 9
二、填空题(4 分×9=36 分)
9.一个三角形有 条边, 个内角, 个顶点, 个外角
10.如图,图中有 个三角形,把它们用符号分别表示为
11.长为 11,8,6,4 的四根木条,选其中三根组成三角形有 种选法,它们分别是
12.如图,在△ABC 中,AE 是中线,AD 是角平分线,AF 是高,则根据图形填空:
⑴BE= =
2
1 ;
⑵∠BAD= =
2
1 ;
⑶∠AFB= =900;
13.在△ABC 中,若∠A=800,∠C=200,则∠B= 0, 若∠A=800,∠B=∠C,则∠C= 0
14.已知△ABC 的三个内角的度数之比∠A:∠B:∠C=1:3:5,则∠B= 0,
∠C= 0
15.如图,在△ABC 中,∠BAC=600,∠B=450,AD 是△ABC 的一条角平分线,
则∠DAC= 0,∠ADB= 0
16.十边形的外角和是 0;如果十边形的各个内角都相等,那么它的一个内角是_______0
17.如图,∠1=∠2=300,∠3=∠4,∠A=800,则 x 0, y 0.
三、解下列各题
18.对下面每个三角形,过顶点 A 画出中线,角平分线和高(4 分×3=12 分)
第(4)题
E
D
C
B
A
第(5)题
D
C
BA
(1) (2) (3) (4) (5) (6)
第(10)题
EDC
B
A
F
第(12)题
E
D CB
A
第(15)题
D CB
A 800
y
x
4
32
1
第(17)题
E
D
CB
A
(1)
CB
A
C B
A
(2)
CB
A
(3)
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
64
19.求出下列图中 x 的值:(4 分×3=12 分)
20.(8 分)一个多边形的外角和是内角和的
7
2 ,求这个多边形的边数
21.在△ABC 中,∠A=
2
1 ∠C=
2
1 ∠ABC, BD 是角平分线,求∠A 及∠BDC 的度数(8 分)
课后反思
多边形巩固练习题
一、判断题.
1.当多边形边数增加时,它的内角和也随着增加.( )
2.当多边形边数增加时.它的外角和也随着增加.( )
3.三角形的外角和与一多边形的外角和相等.( )
4.从 n 边形一个顶点出发,可以引出(n 一 2)条对角线,得到(n 一 2)个三角形.( )
5.四边形的四个内角至少有一个角不小于直角.( )
二、填空题.
1.一个多边形的每一个外角都等于 30°,则这个多边形为 边形.
2.一个多边形的每个内角都等于 135°,则这个多边形为 边形.
3.内角和等于外角和的多边形是 边形.
4.内角和为 1440°的多边形是 .
5.一个多边形的内角的度数从小到大排列时,恰好依次增加相同的度数,其中最小角为 100°,最大的是 140°,
那么这个多边形是 边形.
6.若多边形内角和等于外角和的 3 倍,则这个多边形是 边形.
7.五边形的对角线有 条,它们内角和为 .
8.一个多边形的内角和为 4320°,则它的边数为 .
(1)
x0 x0
(2)
30
xx0
(3)
4x3x
3x 2x
D
CB
A
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
65
9.多边形每个内角都相等,内角和为 720°,则它的每一个外角为 .
10.四边形的∠A、∠B、∠C、∠D 的外角之比为 1:2:3:4,那么∠A:∠B:∠C:∠D= .
11.四边形的四个内角中,直角最多有 个,钝角最多有 个, 锐角最多有 个.
12.如果一个多边形的边数增加一条,那么这个多边形的内角和增加 ,外角和增加 .
三、选择题.
1.多边形的每个外角与它相邻内角的关系是( )
A.互为余角 B.互为邻补角 C.两个角相等 D.外角大于内角
2.若 n 边形每个内角都等于 150°,那么这个 n 边形是( )
A.九边形 B.十边形 C.十一边形 D.十二边形
3.一个多边形的内角和为 720°,那么这个多边形的对角线条数为( )
A.6 条 B.7 条 C.8 条 D.9 条
4.随着多边形的边数 n 的增加,它的外角和( )
A.增加 B.减小 C.不变 D.不定
5.若多边形的外角和等于内角和的和,它的边数是( )
A.3 B.4 C.5 D.7
6.一个多边形的内角和是 1800°,那么这个多边形是( )
A.五边形 B.八边形 C.十边形 D.十二边形
7.一个多边形每个内角为 108°,则这个多边形( )
A.四边形 B,五边形 C.六边形 D.七边形
8,一个多边形每个外角都是 60°,这个多边形的外角和为( )
A.180° B.360° C.720° D.1080°
9.n 边形的 n 个内角中锐角最多有( )个.
A.1 个 B.2 个 C.3 个 D.4 个
10.多边形的内角和为它的外角和的 4 倍,这个多边形是( )
A.八边形 B.九边形 C.十边形 D,十一边形
四、解答题.
1.一个多边形少一个内角的度数和为 2300°.
(1)求它的边数; (2)求少的那个内角的度数.
2.一个八边形每一个顶点可以引几条对角线?它共有多少条对角线?n 边形呢?
3.已知多边形的内角和为其外角和的 5 倍,求这个多边形的边数.
4.若一个多边形每个外角都等于它相邻的内角的
2
1 ,求这个多边形的边数.
5.多边形的一个内角的外角与其余内角的和为 600°,求这个多边形的边数.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
66
6.n 边形的内角和与外角和互比为 13:2,求 n.
7.五边形 ABCDE 的各内角都相等,且 AE=DE,AD∥CB 吗?
8.将五边形砍去一个角,得到的是怎样的图形?
9.四边形 ABCD 中,∠A+∠B=210°,∠C=4∠D.求:∠C 或∠D 的度数.
10.在四边形 ABCD 中,AB=AC=AD,∠DAC=2∠BAC.
求证:∠DBC=2∠BDC.
课题:8.1 二元一次方程组(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1.理解二元一次方程、二元一次方程组及解的概念.
2.会检验一对数是不是某个二元一次方程组的解,会凑数求简单的二元一次方程组的解.
(二)学习重点和难点:
1. 重点:二元一次方程组及解的概念.
2.难点:二元一次方程组的解的概念.
二、问题导读单:阅读 P92—94 页回答下列问题:
1.回答 P93 页中“思考”和本页中“小彩云朵”问题
2.含有_____未知数,并且未知数的______是____,这样的方程叫做一元一次方程.
①5x+2=3x,②x+y=22,③2x+y=40 这三个方程中,___________是一元一次方程
这个方程是一元一次方程,“一元”说的是_________,“一次”说的是_____________
________,所以叫做一元一次方程. 另外两个方程(_______)我们把这样的方程叫做二元一次方程.
“二元”说的是这个方程含有___________即含有 x 和 y,“一次”说的是方程中含有_______的项
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
67
的______都是 1,所以叫做二元一次方程.
3.两个数的和为 18,两个数的差为 6,求这两个数.设这两个数为 x、y.
根据题意,列出两个二元一次方程:
______________=18
______________=6 我们要求的两个数 x 和 y 既要满足第一个方程,又要满足第二方程.因为
同时要满足两个方程,所以我们就把这两个方程合在一起
x+y=____ 像这样两个二元一次方程合在一起,就组成了一个二元一次
______=____ 方程组 交流说明于” ”的作用
4. 仔细研读 P94“探究”并填表.回答问题.说明二元一次方程的解:___________
_______________________________________________________________________
二元一次方程组的解:___________ ________________________________________
_____________________________________________
如方程组 x+y=22 的解是
2x+y=40
三、问题训练单:
5.下面三对数值: x 0,
y 2,
x 2,
y 3,
x 1,
y 5.
(1)满足方程 2x-y=7 的是_______________;(2)满足方程 x+2y=-4 的是______________;
(3)同时满足方程 2x-y=7,x+2y=-4 的是_____________.
6.下面三对数值: x 1,
y 1,
x 2,
y 1,
x 4,
y 5.
(1)是二元一次方程组 2x y 3
3x 4y 10
的解的是______;(2)是二元一次方程组 y 2x 3
4x 3y 1
的解的是___.
7.找一找,二元一次方程组 x y 6
x y 2
的解是______________.
8.下列各对数值中是二元一次方程 x+2y=2 的解是 ( )
A
0
2
y
x B
2
2
y
x C
1
0
y
x D
0
1
y
x
其中是二元一次方程组
22
22
yx
yx 解是 ( )
四、问题生成单:
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
68
五、谈本节课收获和体会:
课题:8.2 消元——二元一次方程组的解法(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 会用代入法解简单的二元一次方程组.(直接代入)
2.初步体会解二元一次方程组的基本思想——“消元”,渗透化归思想.
(二)学习重点和难点:
1. 重点:用代入法解简单的二元一次方程组.
2.难点:体会消元思想.
二、问题导读单:(阅读 P96—98 页回答下列问题)
1.回答 P96 页“思考”______________________________________________________
2.说明 y 为什么可以换成“20-x” ?________________________________________
说明我们在解方程组 x+y=20 时, 二元一次方程组中有____个未知数,如果消
2x+y=40 去其中一个未知数(___),将二元一次方程组转化为我们熟悉的一
元一次方程(只含_____),我们就可以先解出一个未知数( ),然后再设法求另一未知数( ).这种将未知数
的个数由___化___、逐一解决的想法,叫做消元思想.
归纳:上面的解法,是由二元一次方程组中一个方程,将一个未知数用____________
_____________表示出来,再______另一方程,实现______,进而求得这个二元一次方程组的解.
这种方法叫做_______法,简称代入法.
3.细心研读 P97 页例 1 回答“彩云 1”和“彩云 2”问题。(写在教材空白处)总结用代入法解方程
组的步骤为:_____________________________________________
___________________________________________________________________
三、问题训练单:
4.完成下面的解题过程并写出解题对应步骤:(注意解题思路与解题格式书写)
解方程组 ①
②
y 2x 3,
3x 2y 8.
解:把①代入②,得______________. _________________
解这个方程,得 x=______. _________________
把 x=______代入①,得 y=______. ___________________
所以这个方程组的解是 x ____,
y ____ .
_______________________
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
69
2.解方程组 ①
②
2x y 12,
y 3x 2 .
3.解方程组 ①
②
x 1 2y,
2x 3y 2.
4.解方程组
52
3
xy
xy 5.解方程组
13
02
yx
yx
四、问题生成单:
五、谈本节课收获和体会:
课题:8.2 消元——二元一次方程组的解法(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 会用代入法解较简单的二元一次方程组.(移项后代入)
(二)学习重点和难点:
1. 重点:用代入法解较简单的二元一次方程组.
2.难点:代入过程.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
70
(2): ①
②
2x y 5 ,
3x 4y 2.
解:由①,得 y=____________.③
把③代入_____,得_______________.
解这个方程,得 x=_____.
把 x=_____代入_____,得 y=_____.
所以这个方程组的解是 x ____,
y ____ .
①
②
2x y 5,
5x y 9.
(1)
二、问题导读单:(阅读 P96—98 页回答下列问题)
1. 填空:(1)由 y+2x=1,得 y=__________; (2)由 x+2y=1,得 x=__________;
(3)由 2x-y=1,得 y=__________; (4)由 2y-x=1,得 x=__________.
2.完成下面的解题过程:(用代入法解方程组)(结合 P97 页例 1,分析填空)
(1): 2x 3y 2, ①
x 1 2y. ②
解:把②代入①,得________.
解这个方程,得 y=____.
把 y=____代入②得 x=____.
所以这个方程组的解是 x ____ ,
y ____ .
比较两方程的解法,与同学交流说明(2)题中的方程③
是如何得到的?_________________,方程③的是做什么用的?_________________
分析例 1,回答小“彩云 1”问题:_________________________________________“彩云 2”问题:
_________________________________________________________
3.用代入法解下列方程(写出文字说明)
(1)
52
53
yx
yx (3)
1
52
yx
yx
三、问题训练单:
4. 把下列方程写成用含 x 的式子表示 y 的形式:
(1)2x-y=3 _______________ (2)3x+y-1=0 _______________________
5.用代入法解方程组
x-y=3 ① (2)
3x-8y=14 ②
(3)
14
329
mn
nm (4)
qp
qp
45
1332
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
71
(2) x 3y 2, ①
3x 4y 5 0. ②
解:由①,得 x=___________.③
把③代入②,得___________________.
解这个方程,得 y=_____
把 y=4 代入____,得 x=_____.
所以这个方程组的解是 x ____ ,
y ____ .
四、问题生成单:
五、谈本节课收获和体会:
课题:8.2 消元——二元一次方程组的解法(3) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 会用代入法解比较复杂的二元一次方程组.(变形、化简后代入)
(二)学习重点和难点:
1. 重点:用代入法解比较复杂的二元一次方程组.
2.难点:解方程组.
二、问题导读单:(阅读 P96—98 页回答下列问题)
1.填空:(1)由 3x+4y=1,得 y=_____________;(2)由 3x+4y=1,得 x=______________;
(3)由 5x-2y+12=0,得 y=______________;(4)由 5x-2y+12=0,得 x=____________.
2.完成下面的解题过程:用代入法解方程组
(1) x 3y 2, ①
3x 4y 5 0. ②
解:由①,得 x=____________.③
把③代入②,得____________.
解这个方程,得 y=_____.
把 y=_____代入_____,得 x=_____.
所以这个方程组的解是 x ____ ,
y ____ .
3.研读 P97 页例 2.分析回答:所列方程中的(1)x、y 是表示什么?________________
__________________.(2)5x 表示_______________;2y 表示______________
x-y-1=0
3x+y-5=0
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
72
500x 表示_____________________;250y 表示_______________________________
(3)方程①是根据____________________________________相等列出的方程
方程②是根据____________________________________相等列出的方程
(4)在解这个方程组时把方程____变形得到方程③,然后把方程③代入方程_____先消去未知数____
从而解出_____值.
4.分析 P98 页图表,与同学交流说明每个“ ”“ ”的目的和作用。
5.在练习薄上完成 P98 页第 2、3、4 题。
三、问题训练单:
6.将二元一次方程 5x+2y=3 化成用含有 x 的式子表示 y 的形式是 y= ;化成用含有 y 的式子表示 x 的
形式是 x= 。
7.完成下面的解题过程: 用代入法解方程组: ①
②
4x 9y 8,
2x 3y 1.
解法一:由①,得 x=____________.③
把③代入②,得_______________.
解这个方程,得 y=_____.
把 y=____代入,_____得 x=____.
所以这个方程组的解是 x ____ ,
y ____ .
8.用代入法解下列方程组.
(1)
523
32
ts
ts (2)
1187
1365
yx
yx
*(3)
yx
yx
32
153 *(4)
236
244
nm
nm
四、问题生成单:
五、谈本节课收获和体会:
解法二:由②,得 y=____________.③
把③代入①,得_______________________.
解这个方程,得 x=_____.
把 x=_____代入_____,得 y=_____.
所以这个方程组的解是 x ____ ,
y ____ .
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
73
课题:8.2 消元——二元一次方程组的解法(4) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. .会用加减法解简单的二元一次方程组.(直接加减)
2.进一步体会解二元一次方程组的基本思想——“消元”,渗透化归思想.
(二)学习重点和难点:
1. 重点:用加减法解简单的二元一次方程组.
2.难点:加减消元过程.
二、问题导读单:(阅读 P99—102 页回答下列问题)
1.研读 P99 页示例方程组,回答“思考 1”问题__________________________________
2.“小彩云”问题解答:____________________________________________________
3.写出“思考 2”中方程组的解题过程(练习薄上).
4. 加减消元法的概念 把两个二元一次方程的两边分别进行________,就可以消去___________,
得到一个一元一次方程。如果两个二元一次方程中同一未知数的系数______或______时,将两个方
程的两边分别______或______,就能消去这个未知数,得到一个一元一次方程,这种方法叫做加减
消元法,简称___________。
5. 完成下面的解题过程:(用加减法解方程组并与同学生说明为什么用“加”或“减”的)
(1) ①
②
3x 7y 9 ,
4x 7y 5.
解:①+②,得____________.
解这个方程,得 x=____.
把 x=____代入____,得_________,
y=_____.
所以这个方程组的解是 x ____ ,
y ____ .
三、问题训练单:
6.解方程组(直接快速写出方程组的解)
1
5
yx
yx
y
x ;
1
82
yx
yx
y
x ;
12
52
yx
yx
y
x ;
1
52
yx
yx
y
x 。
7.解下列方程组
(1)
924
523
nm
nm (2) (3)
(2) ①
②
3x 7y 9 ,
4x 7y 5.
解:②-①,得____________.
解这个方程,得 x=____.
把 x=____代入____,得_________,
y=_____.
所以这个方程组的解是 x ____ ,
y ____ .
x-y+1=0
3x+y+5=0
x-y=1
3x+y=5
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
74(2)
944
543
nm
nm
解:_______,得___________.
(4)
1523
625
yx
yx (5) ①
②
3x 7y 9 ,
4x 7y 5.
(6) ①
②
6x 7y 19 ,
6x 5y 17.
四、问题生成单:
五、谈本节课收获和体会:
课题:8.2 消元——二元一次方程组的解法(5) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
会用加减法解较简单的二元一次方程组.(乘后加减)
(二)学习重点和难点:
1. 重点:用加减法解较简单的二元一次方程组.
2.难点:用适当的数去乘方程的两边,加减消元.
二、问题导读单:(阅读 P99—101 页回答下列问题)
1.完成下面的解题过程:(用加减法解方程组)
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
75
①
②
(1) ①
②
3x 2y 4 ,
3x 3y 10.
解:①-②,得___________.
解这个方程,得 y=_____.
把 y=__代入__,得______,
x=_____.
所以这个方程组的解是 x ____ ,
y ____ .
分析说明两个方程组中先消去的未知数必需是两方程中同一未知数的___________,如果方程组中
不满足这个条件,你的做法是:__________________________________
2.分析 P100 页中例 3,(1)从“分析”部分我们知道,运用加减法时先使两方程中某同一个未知数的
______________________________________(这也是加减法的条件)
(2)说明方程③和④是为什么变形?各是怎样做的?根据什么?(说与同学) ,其中
①×3、②×2 和③+④三步骤,可以简写成“①×___+___×__” 从而先消去 y.
(3)回答 P100 页中“小彩云”问题并说明为什么?答:___________________________
______________________________________________________________________
3. 用加减法解方程组 ①
②
3x 4y 16 ,
5x 6y 33.
①
②
3x 4y 16 ,
5x 6y 33.
解:①×5,得 _______________. ③
②×3,得 _______________. ④
③-④,得 _______________.
解这个方程,得 y=_____.
把 y=___代入___,得____________,
x=______.
所以这个方程组的解是 x ____ ,
y ____ .
4.写出下列方程组利用加减法(a)消去 x 时方法(b)消去 y 时方法,进行填空.
(1)
944
523
yx
yx ①
②
3x 4y 16 ,
5x 6y 33.
(2)
923
535
yx
yx ①
②
3x 4y 16 ,
5x 6y 33.
(3)
1945
2578
yx
yx ①
②
3x 4y 16 ,
5x 6y 33.
(4)
10514
151213
yx
yx ①
②
3x 4y 16 ,
5x 6y 33.
(a)如: ①×2+② (a)_____________ (a)_____________ (a)_____________
(b)____________ (b)____________ (b)____________ (b)____________
三、问题训练单:
5.用加减法解下面方程组时,你认为先消去哪个未知数较简单,填写消元的方法.
(1) 3 2 15
5 4 23
x y
x y
,消元方法________. (2) 7 3 1
2 3 2
m n
n m
,消元方法_________.
6.用加减法解下列方程组:
(1) 4 2
4 3 6
x y
x y
(2) 3 2 1
4 7
x y
x y
(3) 3 2 5
4 3 1
x y
x y
(4) 4 9
4 10
x y
x y
比较此解法与教材例 3 与上题的解
题过程,你认为哪个更简单?原因
在哪里?
答:_______________________
__________________________
__________________________
__________________________
________
①
②
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
76
四、问题生成单:
五、谈本节课收获和体会:
课题: 8.2 消元——二元一次方程组的解法(6) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 会用加减法解较复杂的二元一次方程组.(先化简方程组)
2.会根据二元一次方程组的特点,选择解法——代入法或加减法.
(二)学习重点和难点:
1. 重点:用加减法解较复杂的二元一次方程组.
2. 难点:根据二元一次方程组的特点,选择解法.
二、问题导读单:(阅读 P101—102 页回答下列问题)
1.细心阅读 P101 页例 4,先填写出“分析”部分的空白处.分析说明:
(1) 列二元一次方程组解应用题的关键是什么?答: 找出两个_________________
(2).请你找出本题的等量关系:
2 台大收割机____小时的工作量+____台小收割机____小时的工作量=3.6
___台大收割机_______的工作量+______小收割机__________的工作量=___
(3)所列方程组进行求解过程中,为什么不先进行消元?先做了什么?这说明什么?
________________________________________________________________________
__________________________________________________ (4)小“纸鉴”的提醒我们做
什么?为什么提醒?
_______________________________________________________________________
2. P102 页的框图,说明什么? 与同学交流说明每个“ ”和“ ”的目的和作用。
3.化简下列方程组
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
77
(1) 3(x 1) y 5
5(y 1) 3(x 5)
得_________;(2)
x 3 y 2 03 4
x 3 y 3 1
4 3 12
得__________.
4. 阅读 P102 页练习框,下部分内容,说明(1)解二元一次方程组有哪几种方法?它们的实质是什
么?答:____________________________________________________
(2)两个方程组分别用什么方法解?与同学交流说明为什么?
三、问题训练单:
5.解答 P102 页练习题中第 2、3 题。
6. 你认为下面的二元一次方程组用哪种方法解比较简单?代入法还是加减法?
(1) y x 3 ,
7x 5y 9 ;
(2) 3x 2y 7 ,
6x 2y 11 ;
(3) 3x 4y 16 ,
5x 6y 33 ;
(4) 3x y 5 ,
5x 2y 15.
7.用加减法解方程组
(1)
x y 1 ,4 2 2
3(2x 5) 4(3y 4) 5.
(2)
x y 1,3 5
3(x y) 2(x 3y) 15.
四、问题生成单:
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
78
分析总结: 列二元一次方程组解
应用题的一般步骤分为:______
___________________________
___________________________
_____
五、谈本节课收获和体会:
课题:8.3 实际问题与二元一次方程组(1) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 经历用方程组解决实际问题的过程,体会方程组是刻画现实世界中含有多个未知数的问题的有
效数学模型;
2.能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列出方程组;
3.体会列方程组比列一元一次方程容易
4.进一步培养学生化实际问题为数学问题的能力和分析问题,解决问题的能力
(二)学习重点和难点:
1. 重点:能根据题意列二元一次方程组;根据题意找出等量关系;
2. 难点:正确发找出问题中的两个等量关系
二、问题导读单:(阅读 P105—106 页回答下列问题)
1.古老的“鸡兔同笼问题”“今有鸡兔同笼,上有三十五头,下有九十四足.问鸡、兔各几何?”
方案一:列一元一次方程解 方案二:列二元一次方程组
设有 x 只鸡,则有( )只兔. 设有 x 只鸡,y 只兔,
根据题意,得 依题意得
_______十__________=94.
比较两种列方程解应用题的方法,说明哪种方法更好列出方程?从中你得到什么启示?
___________________________________________________________________________
2.某校组织 198 名毕业学生到林卡玩,一部分学生坐在草地上唱歌,另一部分学生在河边散步,唱歌的学生是散
步学生的 2 倍还多 10 人.问唱歌、散步的学生各有多少人?
解:设唱歌的学生有 x 人,散步的学生有 y 人.
根据题意,得
____________________________.
3. 某班师生 56 人到某旅游景点参观,教师每张门票 8 元,学生每门票 5 元,共付 304 元.问教师学生各多少人?
解: 设教师 x 人,学生 y 人.根据题意,得
____________________________.
4.时间常用 t 表示,路程常用 s 表示 速度常用 v 表示,则 v= _____,s= ____. t= _____.
哥哥行走的速度是每秒 x 米,弟弟行走的速度是每秒 y 米,则:
(1)走了 16 秒,哥哥走了_____米,弟弟走了____米,哥哥和弟弟一共走了______________米;
(2)走了 2 分钟,哥哥走了____米,弟弟走了____米,哥哥比弟弟多走了_______________米.
5.细心研读 P105 页中“探究一”按要求进行分析和填空.
6.完成下面的解题过程: 某藏药厂生产的珍珠 70 丸有大小盒两种包装,2 大盒 5 小盒共装 50 粒,3 大盒 4 小盒
共装 54 粒.大盒与小盒每盒各装多少粒?
解:设大盒装 x 粒,小盒装 y 粒.
根据题意列方程组,得
_____________________.
解方程组,得____________.
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
79
答:大盒装______粒,小盒装______粒.
三、问题训练单:
7. (列方程组解应用题)篮球比赛中,每场比赛都要分出胜负,每队胜 1 场得 2 分,负 1 场得 1 分.某队为了争取
较好名次,想在全部 22 场比赛中得 40 分,那么这个队胜负场数分别是多少?
8.哥哥弟弟两人相距 48 米,两人同时出发相向而行,16 秒相遇;同时出发同向而行,哥哥 120 秒可追上弟弟.
两人的速度各是多少?设,哥哥走的速度是每秒 x 米,弟弟的速度为每秒 y 米.根据题意列方程组,得
9.运动场的跑道一圈长 400 米.甲练习骑自行车,乙练习跑步,两人从同一处同时出发,4 分钟后两人碰上了;
碰上后两人改为反向出发,40 秒后又碰上了.问两人的速度各是多少?设甲的速度为每分钟 x 米,乙的速度为
每分钟 y 米.根据题意列方程组,得
10. 把一些图书分给某班学生阅读,如果每人分 3 本,则剩余 20 本;如果每人分 4 本,则还缺 25 本.这个班有
多少学生?这些图书共有多少本?设这个班有 x 名学生,这些图书共有 y 本.根据题意列方程组,得
11.有一群鸽子和一些鸽笼,如果每个鸽笼住 6 只鸽子,则剩余 3 只鸽子无鸽笼可住;如果再飞来 5 只鸽子,连
同原来的鸽子,每个鸽笼刚好住 8 只鸽子.原来有多少只鸽子和多少个鸽笼?
设原来有 x 只鸽子和 y 个鸽笼,根据题意列方程组,得
四、问题生成单:
五、谈本节课收获和体会:
课题:8.3 实际问题与二元一次方程组(2) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标: 能够找出实际问题中的已知数和未知数,分析它们之间的数量关系,列
出二元一次方程组,解较简单的行程应用题.
(二)学习重点和难点:
1.重点:列二元一次方程组解较简单的行程应用题.
2.难点:找等量关系列方程组.
二、问题导读单:(阅读 P106 页回答下列问题)
1. 5 辆卡车和 4 辆拖拉机 2 次能运货 68 吨;3 辆卡车和 2 辆拖拉机 3 次能运货 60 吨.问一辆卡车和一辆拖拉机
一次各运货多少吨?设一辆卡车一次运 x 吨,一辆拖拉机一次运货 y 吨
根据题意列方程组,得
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
80
__________________________________
2. 学生在手工实践课中,遇到这样一个问题:要用 20 张白卡纸制作包装纸盒,每张白卡纸可以做盒身 2 个,或
者做盒底盖 3 个,如果 1 个盒身和 2 个盒底盖可以做成一个包装纸盒,那么能否将这些白卡纸分成两部分,一部
分做盒身,一部分做盒底盖,使做成的盒身和盒底盖正好配套?设白卡纸分成两部分,X 张做盒身,Y 张做盒底
盖,使做成的盒身和盒底盖正好配套。
根据题意列方程组,得
__________________________________
3. 12 支球队进行单循环比赛(每队共赛 11 场),规定胜一场得 3 分,平一场得 1 分,负一场得 0 分。若有一
支球队最终的积分为 18 分,那么这个球队平几场?设这支球队共胜 X 场,平 Y 场,则负_______场, 根据题意列
方程组,得
__________________________________
4. 乙组人数是甲组人数的一半,若将乙组人数的三分之一调入甲组,则甲组人数比乙组多 15 人。设甲组原有 x
人,乙组原有 y 人,则可得方程组为 。
5.细心研读 P106 页中“探究二”按要求进行分析和填空.
三、问题训练单:
6. 初一(6)班举办一次集邮展览,展出的邮票比平均每人 3 张多 32 张,比平均每人 4 张少 15 张,求这个班
的学生数及展出邮票的张数。
7*. 木工厂有 28 人,2 个工人一天可以加工 3 张桌子,3 个工人一天可加工 10 只椅子,现在如何安排劳动力,
使生产的一张桌子与 4 只椅子配套?
8*.一外圆凳由一个凳面和三条腿组成,如果 1 立方米木材可制作 300 条腿或制作凳面 50 个,现有 9 立方米的木
材,为充分利用材料,请你设计一下,用多少木材做凳面,用多少木材做凳腿,最多能生产多少张圆凳?
9*.某工厂第一车间比第二车间人数的
5
4 少 30 人,如果从第二车间调出 10 人到第一车间,则第一车间的人数是
第二车间的
4
3 ,问这两车间原有多少人?
解:设第一、第二车间原来分别有 x,y 人
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
81
四、问题生成单:
五、谈本节课收获和体会:
课题: 8.3 实际问题与二元一次方程组(3) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 会列二元一次方程组解百分数应用题.
(二)学习重点和难点:
1. 重点:列二元一次方程组解百分数应用题.
2. 难点:找等量关系列方程组.
二、问题导读单:
1.某市现在的城镇人口为 x 万,农村人口为 y 万.计划一年后城镇人口增加 0.8%,农村人口增加 1.1%,则:(1)
这个市现有总人口是________万;(2)计划一年后城镇人口增加__________万; (3)计划一年后农村人口增加
________万; (4)计划一年后全市人口增加________________万.
2.某市现有 42 万人口,计划一年后城镇人口增加 0.8%,农村人口增加 1.1%,这样全市人口将增加 1%.求这个市
现有的城镇人口与农村人口.
解:设这个市现在的城镇人口 x 万人,农村人口 y 万人.(注意未知数的单位)
根据题意列方程组,得
___________________________
3. 含糖为 10%饮料(我们假设此饮料中主要成分为糖和水,其余不考虑)如果有 100g,那么其中含纯糖为_____g,
含水为________; 含糖为 10%的饮料,如果有 x g, 那么其中含纯糖为_____g,含水为________;现在我们需要
1000 克这种饮料,需要水______克和糖______克.如果现在我们用 400 克水,要配制含糖为 10%的饮料需要纯糖
______克.
4.扎西把含糖为 6%和 12%的两种饮料倒在一起,配成了含糖 8%的混合饮料 240 克.问两种饮料各用了多少克?
解:设需要含糖为 6%的饮料 x 克, 含糖为 12%的饮料 y 克.根据题意列方程组,得
_____________________
5. 某厂 1 月份工业产值 90 万元,比 2 月份少 20%,2 月份工业值多少万元?
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
82
三、问题训练单:
6.书店运来一种儿童故事书,第一天卖了 30%,第二天卖的相当于第一天卖的 120%,比第一天多卖 30 本。书
店运来的这种故事书一共有多少本?
人教版七年级下册数学导学案 设计: 审核: 班级: 姓名:
83
7.某农场仓库运走化肥 162 吨,又运进 142 吨,
这时仓库里的化肥比原来少 5%,仓库里原来
有化肥多少吨?
8*.沙洲造纸厂第一季度,每月的新闻纸产量都
比前一个月增产 10%,已经知二月份产新闻纸
220 吨,求第一个月与第三个月份各产新闻纸
多少吨?
9*.红水乡修一条长 2400 米的水渠,第一周修
了全长的 37.5%,第二周又修了剩余的 11/20,
还要修多少米才能完成任务?
10*.师徒两人共同加工一批零件,完成任务时,
师傅加式了这批零件的 65%,徒北比师傅少加
工 24 件,师徒共加工多少个零件?
11*.小明看一本书,第一天看了全书的 40%,第
2 天看了全书的三分之一,第三天看了 80 页正
好看完.这本书共有多少页?
12*.,仓顶小学男学生的人数和女学生的人数
的 60%正好相等,已知这个学校有男生 480 人,
求这个学校共有学生多少人?
84
四、问题生成单:
五、谈本节课收获和体会:
课题:8.3 实际问题与二元一次方程组(4) 月 日 班级: 姓名:
一、教材分析:
(一)学习目标:
1. 进一步经历用方程组解决实际问题的过程,体会方程组是刻画现实世界的有效数学模
型;
2、会用列表的方式分析问题中所蕴涵的数量关系,列出二元一次方程组;
3、培养分析问题、解决问题的能力,进一步体会二元一次方程组的应用价值.
(二)学习重点和难点:
1. 重点:借助列表分问题中所蕴含的数量关系.
2. 难点:用列表的方式分析题目中的各个量的关系。
二、问题导读单:(阅读 P106--107 页回答下列问题)
1. 某农场 300 名职工耕种 51 公顷土地,计划种植
水稻、棉花、和蔬菜,已知种植植物每公顷所需的
劳动力人数及投入的设备奖金如下表:已知该农场
计划在设备投入 67 万元,应该怎样安排这三种作
物的种植面积,才能使所有职工都有工作,而且投
农作物
品种
每公顷需
劳动力
每公顷需
投入奖金
水稻 4 人 1 万元
棉花 8 人 1 万元
蔬菜 5 人 2 万元
85
入的资金正好够用?
问题:(1)题中有几个已知量?说明各量的具体含意
(与同学交流) (2) 题中求什么?________________________________
解 : 设
___________________________________________________________________________
根据题意列方程组得:
__________________________________
2. 小明去帮学校购买体育用品,足球每只 100 元,篮球每只 60 元, 共购买了 20 只球,用去
1680 元 . 你 能 求 出 足 球 、 篮 球 各 买 了 多 少 只 吗 ? 设
_______________________________________
根据题意列方程组得:
__________________________________
3. 某运输队送一批货物,计划 20 天完成,实际每天多运送 5 吨,结果不但提前 2 天完成
任务并多运了 10 吨,求这批货物有多少吨?原计划每天运输多少吨?
解: 设_______________________________________
根据题意列方程组得:
__________________________________
4.跃进村去年粮食总产量为 180 万千克,今年争取比去年增长一成半,今年粮食总产量可达
到多少万千克? 解: 设_______________________________________
根据题意列方程组得:
__________________________________
5.细心研读 P106 页中“探究三”按要求进行分析和填空.并说明解出方程组的解后还要考
虑 什 么 ?
_____________________________________________________________________
三、问题训练单:
6. 2 辆大卡车和 5 辆小卡车工作 2 小时可运送垃圾 36 吨,3 辆大卡车和 2 辆小卡车工
作 5 小时可运输垃圾 80 吨,那么 1 辆大卡车和 1 辆小卡车各运多少吨垃圾。
解: 设_______________________________________
根据题意列方程组得:
__________________________________
7. 甲乙两地相距 60 千米,A、B 两人骑自行车分别从甲乙两地相向而行,如果 A 比 B 先出
发半小时,B 每小时比 A 多行 2 千米,那么相遇时他们所行的路程正好相等。求 A、B 两人
骑自行车的速度。解: 设_______________________________________
根据题意列方程组得:
__________________________________
8.已知甲、乙两种商品的原价和为 200 元。因市场变化,甲商品降价 10%,乙商品提高 10%,
调价后甲、乙两种商品的单价和比原单价和提高了 5%。求甲、乙两种商品的原单价各是多
少元。
解: 设_______________________________________
86
根据题意列方程组得:
__________________________________
9.一批蔬菜要运往某批发市场,菜农准备租用
汽车公司的甲、乙两种货车.已知过去两次租
用这两种货车的记录如下表所示.
这批蔬菜需租用 5 辆甲种货车、2 辆乙种
货车刚好一次运完,如果每吨付 20 元运费,
问:菜农应付运费多少元?
四、问题生成单
五、谈本节课收获和体会:
课题:第八章二元一次方程组复习(1-2) 月 日 班级: 姓名:
一、学习目标:
1. 知道第八章二元一次方程组知识结构图.
2.通过基本训练,巩固第八章所学的基本内容.
3.通过典型例题和综合运用,加深理解第八章所学的基本内容,发展能力.
二、学习重点和难点:
1.重点:知识结构图和基本训练.
2.难点:典型例题和综合运用.
三、归纳总结,完善认知:(阅读 P117 页及全章内容回答下列问题)
1.在方框内填写相应的文字
甲种货车
(辆)
乙种货车
(辆)
总 量
(吨)
第 1 次 4 5 28.5
第 2 次 3 6 27
�
方程组方法
�
实际问题的答案
�
答
�
方程组的解
�
(消元)
�
加减法
�
代入法
�
解
�
方
�
程
�
组
�
二元一次方程组
�
审题、设未知数、列方程组
�
实际问题
87
此框图说明什么?____________________________________________________
四、基本训练,掌握双基
1.填空: (1)含有_____个未知数,并且含有未知数的项的次数都是_____,像这样的方
程叫做二元一次方程.
(2)把具有相同未知数的两个二元一次方程合在一起,就组成了一个_________.
(3)既满足第一个二元一次方程,又满足第二个二元一次方程的两个未知数的值,叫做
___________________.
(4)二元一次方程组中有两个未知数,如果消去其中一个未知数,那么就把二元一次方程组
转化为我们熟悉的_______________方程,我们可以先求出一个未知数,然后再求另一个未
知数.这种将未知数的个数由多化少、逐一解决的思想,叫做_________思想.
(5)把二元一次方程组中的一个方程的一个未知数用含另一个未知数的式子表示出来,再代入
另一个方程,实现消元,进而求得这个二元一次方程组的解.这种方法叫做______________
法,简称________法.
(6)两个二元一次方程中同一个未知数的系数相反或相等时,把这两个方程的两边分别相加或
相减,就能消去未知数,得到一个一元一次方程.这种方法叫做______________法,简称
________法.
(7)用二元一次方程组解应用题一般有五步:________、设未知数、__________、解方程
组、答.
2.在 x 2
y 2
与 x 1
y 1
两组值中,是二元一次方程组 x y 0
2x y 3
的解的是 =
y=_____.
x _____ ,
3.完成下面的解题过程: 4.用代入法解方程组 5x y 110,
9y x 110.
用代
入法解方程组 ①
②
x y 4,
4x 2y 1.
解:由①,得 x=____________.③
把③代入②,得_______________.
解这个方程,得 y=_____.
把 y=_____代入③,得 x=_____.
所以这个方程组的解是 x ____ ,
y ____ .
88
5.完成下面的解题过程: 6.用加减法解方程组 0.6x 0.4y 1.1,
0.2x 0.4y 2.3.
用加减法解方程组 ①
②
5x 2y 9,
2x 6y 7.
解:①×3,得_________________.③
②+③,得________________.
x=______.
把 x=______代入____,得__________,
y=______.
所以这个方程组的解是 x ____ ,
y ____ .
7.解方程组
2(x y) x y 1,3 4
6(x y) 4(2x y) 16.
五、综合运用,发展能力
8. 已知二元一次方程组 ax by 4
bx ay 2
的解是 x 1
y 2
,求 a、b 的值.
9. 2 台大收割机和 5 台小收割机都工作 2 小时共收割青稞 3.6 公顷,3 台大收割机和 2 台
小收割机都工作 5 小时共收割青稞 8 公顷.1 台大收割机和 1 台小收割机每小时各收割青
稞多少公顷?
89
10.填空:已知二元一次方程组 x my 4
nx 3y 2
的解是 x 1
y 3
,则 m=_____,n=_____.
11.填空:某班学生共 40 人,男生比女生少 3 人,问男女生各多少人?设男生 x 人,女生
y 人.根据题意列方程组,得 _________________ ,
_________________ .
12.填空:2 本练习本及 3 支铅笔的价格为 3.2 元,4 本练习本和 5 支铅笔的价格为 5.8 元.
问一本练习本和一支铅笔的价格各为多少?设一本练习本的价格为 x 元,一支铅笔的价
格为 y 元.根据题意列方程组,得 _________________ ,
_________________ .
13.填空:某班上数学课的时候,准备分组讨论.如果每组 7 人,则余下 3 人;如果每组 8
人,则又不足 5 人.问全班有多少人?要分几组?设全班有 x 人,要分 y 组.根据题意列
方程组,得 _________________ ,
_________________ .
14.填空:某家存入银行甲、乙两种不同性质的存款 20 万元,甲种存款的年利率为 2.4%,
乙种存款的年利率为4.6%,该家一年共得利息7800元.求甲、乙两种存款各是多少万元?
设 甲 、 乙 两 种 存 款 各 是 x 万 元 、 y 万 元 . 根 据 题 意 列 方 程 组 , 得
_______________________ ,
_______________________ .
15.列二元一次方程组解应用题:
(1) 根据市场调查,常觉大盒装(每盒 10 粒)和小盒装(每盒 6 粒)两种产品的销售
量(按盒计算)比为 2:5.某藏药厂每天生产常觉 7000 粒,问应分装大、小盒两种产品
各多少盒?
(2)*.某校六年级有三个班,甲班人数是乙数的 1 又 2/5 倍,乙班比丙少 20%,甲班有 56
人,六年级共有多少人?
90
(3)*. 某水库,有流入一定量的水不断地流进来,按现在的放水量,水库中的水可使用 80 天,
但最近日益增加,流入量减少 20%,按现在的放水量放水,只能使用 60 天,问现在的流入量和
放水量分别为多少? .设每天流入的水量为 X,放出的水量为 Y,水库的蓄水量为 a,
(4)*. 某校体操队和篮球队的人数是 5:6,排球队的人数比体操队的人数 2 倍少 5 人,
篮球队的人数与体操队的人数的 3 倍的和等于 42 人,求三种队各有多少人?
16.完成下面的探究过程:打折前,买 60 件 A 商品和 30 件 B 商品用了 1080 元,买 50 件 A
商品和 10 件 B 商品用了 840 元.打折后,买 500 件 A 商品和 500 件 B 商品用了 9600 元,
比不打折少花多少钱?设打折前买 1 件 A 商品需要 x 元,买 1 件 B 商品需要 y 元.根据题
意列方程组,得 ______________________ ,
______________________ .
解方程组,得 x ________ ,
y ________ .
这就是说,打折前,买 1 件 A 商品需要_____元,买 1 件 B 商品需要_____元.因此,打折前,
买 500 件 A 商品和 500 件 B 商品需要_____元.因此,买 500 件 A 商品和 500 件 B 商品,打
折后比打折前可以少花_____元.
91