北师大版七年级上册-第二章有理数及其运算
一、填空题
1.如果提高 10 分表示+10 分,那么下降 8
分表示_______,不升不降用_______表示.
2.如果向南走 5 km 记为-5 km,那么向北
走 10 km 记为_______.
3.如果收入 2 万元用+2 万元表示,那么支
出 3000 元,用_______表示.
4.某乒乓球比赛用+1 表示赢一局,那么输 2
局用_______表示,不输不赢用_______表
示.
5.某企业以 1996 年的利润为标准,2000 年
增加了 10%记为+10%,2001 年利润为-5%
表示的意义是_______.
6.节约用水,如果节约 5.6 吨水记作+5.6 吨,
那么浪费 3.8 吨水,记作_______.
二、选择题
1.下面是关于 0 的一些说法,其中正确说法
的个数是( )
①0 既不是正数也不是负数;②0 是最
小的自然数;③0 是最小的正数;④0 是最
小的非负数;⑤0 既不是奇数也不是偶数.
A.0 B.1 C.2 D.3
2.下列各数,正数一共有( )
-11,0,0.2,3,+
7
1 ,
3
2 ,1,-1
A.5 个 B.6 个 C.4 个 D.3 个
3.在 0,
2
1 ,-
5
1 ,-8,+10,+19,+3,
-3.4 中整数的个数是( )
A.6 B.5C.4 D.3
三、判断题
1.零上 5℃与零下 5℃意思一样,都是 5℃.
()
2.正整数集合与负整数集合并在一起是整
数集合.( )
3.若-a 是负数,则 a 是正数.( )
4.若+a 是正数,则-a 是负数.( )
5.收入-2000 元表示支出 2000 元.( )
四、能力拓展题
某地气象站测得某天的四个时刻气温分
别为:早晨 6 点为零下 3℃,中午 12 点为零
上 1℃,下午 4 点为 0℃,晚上 12 点为零下 9
℃.
1.用正数或负数表示这四个不同时刻
的温度.
2.早晨 6 点比晚上 12 点高多少度.
3.下午 4 点比中午 12 点低多少度.
五、下表是 2003 年 4 月 19 日《信息早报》
上刊登的几支股票的涨跌情况,请看
代码
股
票
名
称
昨收
盘 今收盘 涨跌
(%)
600828
成
商
集
团
8.83 9.71 +9.97
600829
天
鹅
股
份
10.43 10.65 +2.11
600830
大
红
鹰
11.14 11.30 +1.44
600831
广
电
网
络
21.88 21.58 -1.37
600832
东
方
明
珠
18.81 18.61 -1.06
600833
第
一
医
药
8.76 9.20 +5.02
600834
申
通 10.87 10.87 0.00
地
铁
600835
上
菱
电
器
13.47 13.31 -1.19
表中出现了比 0 还小的数,我们可以
用带有“-”号(读作负)的数来表示,
如-1.06;这说明该支股票当天收盘价与昨
天的收盘价相比下跌了 1.06%;前面带“+”
号的说明该支股票与昨天的收盘价比较涨
了百分之多少.0 表示不涨不跌.
你观察一下有哪些股票跌了_______.
思考:冰糕要保持不融化需要的温度
比 0℃高还是低?
答:________________.
一、填空题
1.大于-5.1 的所有负整数为_____.
2._____既不是正数,也不是负数.
3.分数有_____,_____.
4.珠穆朗玛峰高出海平面 8848 米,表示为
+8848 米.吐鲁番盆地低于海平面 155 米,表
示为____.
5.请写出 3 个大于-1 的负分数_____.
6.某旅游景点一天门票收入 5000 元,记作
+5000 元,则同一天支出水、电、维修等各
种费用 600 元,应记作_____.
7.某县外贸局一年出口总额人民币 1300 万
元,表示为+1300 万.进口某种原料 350 万
应表示为_____.
8.在“学雷锋活动月”活动中,甲乙两组同
学上街清扫街道,它们分别在街道的两端
同时相向开始打扫,街道总长 1200 米,两
组会合时甲组向南清扫了 500 米,记作+500
米,则乙组向北清扫了_____米,应记作
_____.
9.某下岗职工购进一批苹果,第一天盈利
17 元,记作+17 元,第二天亏损 6 元应记
作_____.
二、选择题
10.下列各数中,大于-
2
1 小于
2
1 的负数是
( )
A.-
3
2 B.-
3
1 C.
3
1 D.0
11.负数是指( )
A.把某个数的前边加上“-”号
B.不大于 0 的数
C.除去正数的其他数
D.小于 0 的数
12.关于零的叙述错误的是( )
A.零大于所有的负数 B.零小于所有的正
数
C.零是整数 D.零既是正数,也是负
数
13.非负数是( )
A.正数 B.零 C.正数和零 D.自然数
14.文具店、书店和玩具店依次座落在一条
东西走向的大街上,文具店在书店西边 20
米处,玩具店位于书店东边 100 米处,小
明从书店沿街向东走了 40 米,接着又向东
走了-60 米,此时小明的位置在( )
A.文具店 B.玩具店
C.文具店西 40 米处 D.玩具店西 60 米处
三、解答题
15.下面是具有相反意义的量,请用箭头标
出其对应关系
16.某天气预报显示,我国五个地区的最高
气温第二天比第一天下降了 12℃,这五个
地区第一天最高气温如图所示,请填写第
二天的最高气温
17.某人向东走了 4 千米记作+4 千米,那么
-2 千米表示什么?
18.某同学语、数、外三科的成绩,高出平
均分部分记作正数,低出部分记作负数,
如表所示
科目 语文 数学 外语
成绩 +15 -3 -6
请回答,该生成绩最好和最差的科目
分别是什么?
19.某公司今年第一季度收入与支出情况如
表所示(单位:万元)
月份 一月 二月 三月
收入 32 48 50
支出 12 13 10
请问:(1)该公司今年第一季度总收入
与总支出各多少万元?
(2)如果收入用正数表示,则总收入与
总支出应如何表示?
(3)该公司第一季度利润为多少万元?
同学们都会读温度计吧?
同温度计类似,可以在一条直线上画
出刻度标上数,用直线上的点表示有理数.
定义:画一条水平直线,在直线上取
一点,表示 0(叫做原点)选取某一长度为
单位长度,规定直线上向右的方向为正方
向,就得到一条数轴,画数轴的具体方法:
1.画直线(一般水平方向),标出一点为原
点 0.
2.规定从原点向右的方向为正方向,那么向
左方为负方向.
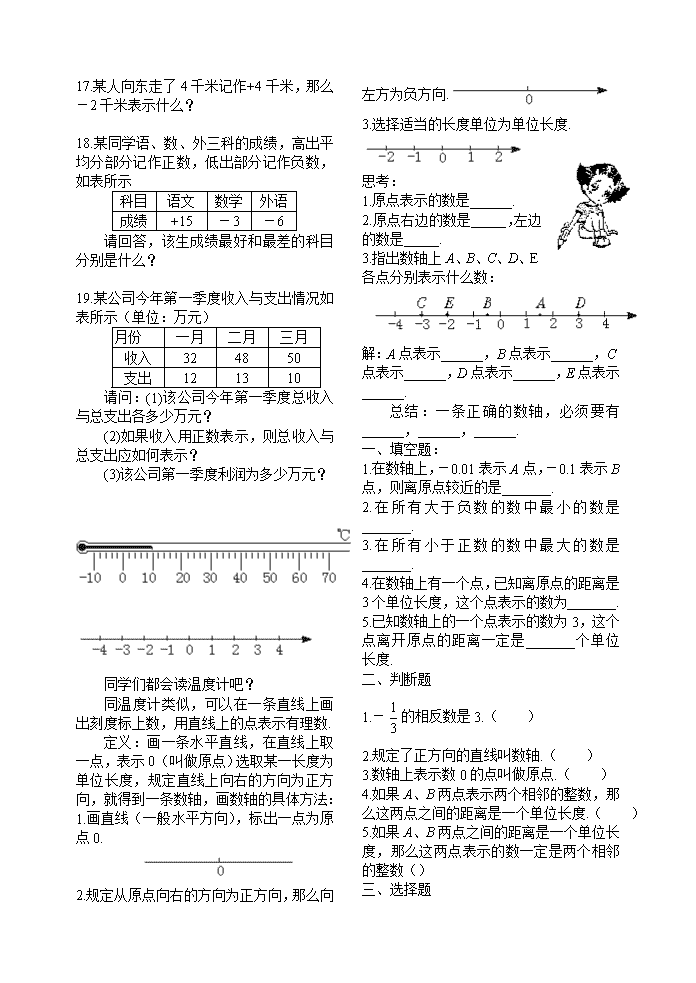
3.选择适当的长度单位为单位长度.
思考:
1.原点表示的数是______.
2.原点右边的数是_____,左边
的数是_____.
3.指出数轴上 A、B、C、D、E
各点分别表示什么数:
解:A 点表示______,B 点表示______,C
点表示______,D 点表示______,E 点表示
______.
总结:一条正确的数轴,必须要有
______,______,______.
一、填空题:
1.在数轴上,-0.01 表示 A 点,-0.1 表示
B 点,则离原点较近的是_______.
2. 在 所 有 大 于 负 数 的 数 中 最 小 的 数 是
_______.
3. 在 所 有 小 于 正 数 的 数 中 最 大 的 数 是
_______.
4.在数轴上有一个点,已知离原点的距离是
3 个单位长度,这个点表示的数为_______.
5.已知数轴上的一个点表示的数为 3,这个
点离开原点的距离一定是_______个单位
长度.
二、判断题
1.-
3
1 的相反数是 3.( )
2.规定了正方向的直线叫数轴.( )
3.数轴上表示数 0 的点叫做原点.( )
4.如果 A、B 两点表示两个相邻的整数,那
么这两点之间的距离是一个单位长度.
( )
5.如果 A、B 两点之间的距离是一个单位长
度,那么这两点表示的数一定是两个相邻
的整数()
三、选择题
1.每个有理数都可以用数轴上的以下哪项
来表示( )
A.一个点 B.线 C.单位 D.长度
2.下列图形中不是数轴的是( )
3.下列各式中正确的是( )
A.-3.14<-πB.-1
2
1 >-1
C.3.5>-3.4D.-
2
1 <-2
4.下列说法错误的是( )
A.零是最小的整数
B.有最大的负整数,没有最大的正整数
C.数轴上两点表示的数分别是-2
3
1 与-
2,那么-2 在右边
D.所有的有理数都可以用数轴上的点表示出来
四、下图是一个长方体纸盒的展开图,请
把-5,3,5,-1,-3,1 分别填入六个长方形,
使得按虚线折成长方体后,相对面上的两
数互为相反数.
一、填空题
1.若数轴规定了向右为正方向,则原点表示
的数为______,负数所对应的点在原点的
______,正数所表示的点在原点的______.
2.在数轴上 A 点表示-
3
1 ,B 点表示
2
1 ,则
离原点较近的点是_____.
3.两个负数较大的数所对应的点离原点较
____.
4.在数轴上距离原点为 2 的点所对应的数
为_____,它们互为_____.
5.数轴上 A、B、C 三点所对应的实数为-
3
2 ,-
4
3 ,
5
4 ,则此三点距原点由近及远
的顺序为_____.
6.数轴上-1 所对应的点为 A,将 A 点右移
4 个单位再向左平移 6 个单位,则此时 A 点
距原点的距离为_____.
7.一个数与它的相反数之和等于_____.
8.比较大于(填写“>”或“<”号)
(1)-2.1_____1 (2)-3.2_____-4.3
(3)-
2
1 _____-
3
1 (4)-
4
1 _____0
9.相反数是它本身的数为_____.
二、选择题
10.下面正确的是( )
A.数轴是一条规定了原点,正方向和长
度单位的射线
B.离原点近的点所对应的有理数较小
C.数轴可以表示任意有理数
D.原点在数轴的正中间
11.关于相反数的叙述错误的是( )
A.两数之和为 0,则这两个数为相反数
B.如果两数所对应的点到原点的距离相
等,这两个数互为相反数
C.符号相反的两个数,一定互为相反数
D.零的相反数为零
12.如果点 A、B、C、D 所对应的数为 a、b、
c、d,则 a、b、c、d 的大小关系为( )
A.a<c<d<bB.b<d<a<c
C.b<d<c<aD.d<b<c<a
13.下列表示数轴的图形中正确的是( )
14.若数轴上 A、B 两点所对应的有理数分
别为 a、b,且 B 在 A 的右边,则 a-b 一
定( )
A.大于零 B.小于零
C.等于零 D.无法确定
三、解答题
15.写出大于-4.1 小于 2.5 的所有整数,并
把它们在数轴上表示出来.
16.请指出下列各数的相反数,并把它们在
数轴上表示出来
3,
2
1 ,0,-2
2
1
17.已知 a 是最小的正整数,b 的相反数还
是它本身,c 比最大的负整数大 3,计算
(2a+3c)·b 的值.
在给出的数轴上,标出以下各数及它
们的相反数.-1,2,0,
2
5 ,-4
观察以上各数在数轴上的位置,回答:
距原点一个单位长度的数是________
距 原点 2 个 单位 长度 的数 是_______和
________距原 点
2
5 个单 位长 度._____ 和
______距原点 4 个单位长度距原点最近的
是________.
像 1,2,
2
5 ,4,0 分别是±1,±2,
±
2
5 ,±4,0 的绝对值.在数轴上,一个数
所对应的点与原点的距离叫该数的绝对值.
如:+2 的绝对值是 2,记作|+2|=2
-2 的绝对值是 2,记作|-2|=2
因此绝对值是 2 的数有_____个,它们
是_____,绝对值是
10
1 的数有_____个,它
们 是 _____ , 那 么 0 的 绝 对 值 记 作 |
|=_____,-100 的绝对值是_____,记作|
|=_____.
思考:一个数的绝对值能是负数吗?
一、填空题
1. 一 个 数 a 与 原 点 的 距 离 叫 做 该 数 的
_______.
2.-|-
7
6 |=_______,-(-
7
6 )=_______,
-|+
3
1 |=_______,-(+
3
1 )=_______,
+|-(
2
1 )| =_______,+(-
2
1 )=_______.
3.____的倒数是它本身,___的绝对值是它
本身.
4.a+b=0,则 a 与 b_______.
5.若|x|=
5
1 ,则 x 的相反数是_______.
6.若|m-1|=m-1,则 m___1.
若 |m - 1|>m - 1, 则 m___1. 若 |x|=| - 4|, 则
x=____.
若|-x|=|
2
1 |,则 x=______.
二、选择题
1.|x|=2,则这个数是( )
A.2 B.2 和-2 C.-2D.以上都错
2.|
2
1 a|=-
2
1 a,则 a 一定是( )
A.负数 B.正数 C.非正数 D.非负数
3.一个数在数轴上对应点到原点的距离为
m,则这个数为( )
A.-mB.m C.±mD.2m
4.如果一个数的绝对值等于这个数的相反
数,那么这个数是( )
A.正数 B.负数 C.正数、零 D.负数、零
5.下列说法中,正确的是( )
A.一个有理数的绝对值不小于它自身
B.若两个有理数的绝对值相等,则这两个数相等
C.若两个有理数的绝对值相等,则这两个数
互为相反数
D.-a 的绝对值等于 a
三、判断题
1.若两个数的绝对值相等,则这两个数也相等.( )
2.若两个数相等,则这两个数的绝对值也相等
( )
3.若 x
0,b<0,则 a+b>0.( )
2.若 a+b<0,则 a,b 两数可能有一个正数.
( )
3.若 x+y=0,则|x|=|y|.( )
4.有理数中所有的奇数之和大于 0.( )
5. 两 个 数 的和 一 定 大 于 其 中一 个 加 数.
( )
三、选择题
1.有理数 a,b 在数轴上对应位置如图所示,
则 a+b 的值为( )
A.大于 0B.小于 0
C.等于 0D.大于 a
2.下列结论不正确的是( )
A.若 a>0,b>0,则 a+b>0
B.若 a<0,b<0,则 a+b<0
C.若 a>0,b<0,则|a|>|b|,则 a+b>0
D.若 a<0,b>0,且|a|>|b|,则 a+b>0
3.一个数大于另一个数的绝对值,则这两个
数的和是( )
A.负数 B.正数 C.非负数 D.非正数
4.如果两个数的和为正数,那么( )
A.这两个加数都是正数 B.一个数为
正,另一个为 0
C.两个数一正一负,且正数绝对值大 D.
必属于上面三种之一
四、解答题
一辆货车从货场 A 出发,向东走了 2 千米
到达批发部 B,继续向东走 1.5 千米到达商
场 C,又向西走了 5.5 千米到达超市 D,最
后回到货场.
(1)用一个单位长度表示 1 千米,以东为
正方向,以货场为原点,画出数轴并在数
轴上标明货场 A,批发部 B,商场 C,超市
D 的位置.
(2)超市 D 距货场 A 多远?
(3)货车一共行驶了多少千米?
五、长江足球队近六年与黄河队比赛如下
表:
表 1 长江足球队成绩
其中用-x 表示净输 x 个球.用+x 表示
净赢 x 个球.用 0 表示平局.
请您帮忙计算一下以上六年合计分别是多
少?
1997 年 : ________ 1998 年 :
________
1999 年:________ 2000 年:________
2001 年:________ 2002 年:________
六年净胜球总计:_________.
思考:以上结果你是如何得出的?
(1)同号两数如何相加?
(2)异号两数如何相加?
(3)一个数与零相加和是多少?
参考例题
[例 1]仓库内原存粮食 4000 千克,一周
内存入和取出情况如下(存入为正,单位:
千克):
2000,-1500,-300,600,500,-1600,-200
问第 7 天末仓库内还存有粮食多少千克?
解 : 2000+( - 1500)+( -
300)+600+500+( - 1600)+( -
200)=2000+600+[(-1500)+(-1600)]+[(-
300)+500+( - 200) ] =2600+( - 3100)= -
500(千克)材
4000+(-500)=3500(千克)
答:第 7 天末仓库内还存有粮食 3500
千克.
[例 2]从一批货物中抽取 20 袋,称得它
们的重量如下:(单位:千克)
122,121,119,118,122,123,120,
118,124,122,119,121,124,117,119,
123,124,122,118,116.
计算这批货物的总重量和每袋的平均
重量.(答案:2412 千克 120.6 千克.)
一、填空题
1 、 1 - 0=_____,0 - 1=_____,0 - ( -
2)=_____.
2、a-_______=0,-b-_______=0.
3、( )-(-10)=20,-8-( )=-15.
4、比-6 小-3 的数是_______.
5.、-1
7
2 比 1
7
1 小_______.
6.两个正数之和为_____,两个负数之和为
_____,一个数同 0 相加得_____.
7.某地傍晚气温为-2℃,到夜晚下降了 5
℃,则夜晚的气温为_____,第二天中午上
升了 10℃,则此时温度为_____.
8.已知一个数是-2,另一个数比-2 的相
反数小 3,则这两个数和的绝对值为_____.
二、选择题
1.若 x-y=0,则( )
A.x=0B.y=0C.x=yD.x=-y
2.若|x|-|y|=0,则( )
A.x=yB.x=-yC.x=y=0D.x=y 或 x=-y
3.-(-
2
1 -
3
1 )的相反数是( )
A. -
2
1 -
3
1 B. -
2
1 +
3
1 C.
2
1 -
3
1
D.
2
1 +
3
1
4.下列结论不正确的是( )
年份 97 98 99 00 01 02
一场 +3 +2 -2 -1 +4 0
二场 +1 -3 +3 -4 0 -1
合计
A.两个正数之和必为正数
B.两数之和为正,则至少有一个数为正
C.两数之和不一定大于某个加数
D.两数之和为负,则这两个数均为负
数
5.下列计算用的加法运算律是( )
-
3
2 +3.2-
3
2 +7.8=-
3
1 +(-
3
2 )+3.2+7.8
=-(
3
1 +
3
2 )+3.2+7.8=-1+11=10
A.交换律 B.结合律
C.先用交换律,再用结合律
D.先用结合律,再用交换律
6.若两个数绝对值之差为 0,则这两个数
( )
A.相等 B.互为相反数
C.两数均为 0D.相等或互为相反数
7.-[0.5-
3
1 -(
6
1 +2.5-0.3)]等于( )
A.2.2B.-3.2C.-2.2D.3.2
三、判断题
1.1-a 一定小于 1.( )
2.若对于有理数 a,b,有 a+b=0,则 a=0,b=0
( )
3.两个数的和一定大于每一个加数.( )
4.a>0,b<0,则 a-b>a+b.( )
5.若|x|=|y|,则 x-y=0.( )
四、解答题
1.两个加数的和是-10,其中一个加数是-
10
2
1 ,则另一个加数是多少?
2.某地去年最高气温曾达到 36.5℃,而冬季
最低气温为-20.5℃,该地去年最高气温比
最低气温高多少度?
3.已知 a=-
8
3 ,b=-
4
1 ,c=
4
1 ,求代数式 a-b
-c 的值.
4.一个数的相反数的绝对值等于这个数的
绝对值的相反数,问这个数是多少?
5.弘文中学定于十一月份举行运动会,组委
会在整修百米跑道时,工作人员从 A 处开
工,约定向东为正,向西为负,从开工处
A 到收工处 B 所走的路线(单位:米),
分别为+10、-3、+4、-2、+13、-8、
-7、-5、-2,工作人员整修跑道共走了
多少路程?
一、计算题
1、+3-(-7)=_______.
2、(-32)-(+19)=_______.
3、-7-(-21)=_______.
4、(-38)-(-24)-(+65)=_______.
二、填空题
1、-4-_______=23.
2、36℃比 24℃高___℃,19℃比-5℃高
___℃.
3、A、B、C 三点相对于海平面分别是-
13 米、-7 米、-20 米,那么最高的地方
比最低的地方高_______米.
4、冬季的某一天,甲地最低温度是-15
℃,乙地最低温度是 15℃,甲地比乙地低
_______℃.
三、已知:a=-2,b=20,c=-3,且 a-(-b)+c
-d=10,求 d 的值.
四、有十箱梨,每箱质量如下:(单位:千
克)
51,53,46,49,52,45,47,50,53,
48
你能较快算出它们的总质量吗?列式计算.
五、某汽车厂计划半年内每月生产汽车 20
辆,由于另有任务,每月上班人数不一定
相等,实际每月生产量与计划量相比情况
如下表(增加为正,减少为负).
月份 一 二 三 四 五 六
增减(辆) +3 -2 -1 +4 +2 -5
1.生产量最多的一天比生产量最少的
一天多生产多少辆?
2.半年内总生产量是多少?比计划多
了还是少了,增或减多少?
六、计算:
(1)23-17-(-7)+(-16)(2)
3
2 +(-
5
1 )-1+
3
1
(3)(-26.54)+(-6.4)-18.54+6.4
(4)(-4
8
7 )-(-5
2
1 )+(-4
4
1 )-3
8
1
(5)0+1-[(-1)-(-
7
3 )-(+5)-(-
7
4 )]+|-4|
七、有一架直升飞机从海拔 1000 米的高原
上起飞,第一次上升了 1500 米,第二次上
升上-1200 米,第三次上升了 1100 米,第
四次上升了-1700 米,求此时这架飞机离
海平面多少米?
3.10 名学生体检测体重,以 50 千克为基准,
超过的数记为正,不足的数记为负,称得
结果如下(单位:千克):
2,3,-7.5,-3,5,-8,3.5,4.5,8,-1.5
这 10 名学生的总体重为多少?10 名学
生的平均体重为多少?
一、填空题
1.23-|-6|-(+23)=_______.
2.-7+4-(-2)=_______.
3.把(+2)+(-5)-(+3)-(-1)写
成省略括号的和的形式是_______.
4.-5 减去-3 的相反数得_______.
5.小明从家里出发向东行驶 2 千米,记作+2
千米,再向西行驶 3 千米,记作-3 千米,
实际结果是_______.
6.已知:a=11,b=-12,c=-5
计算:(1)a+b+c=_____(2)a-b+c=_____
(3)a-(b+c)=_____(4)b-(a-
c)=_____
7.某次考试初一年级数学平均分为 73 分,
其中最高分高出平均分 25 分,最低分比平
均分低 24 分,请问最高分比最低分高_____
分.
8.某地上午气温为 5℃,中午气温上升 7℃,
晚上 又下降了 16 ℃,则 晚上的气 温为
______.
二、选择题
1.若 m<0,则 m 与它的 5 倍的相反数的差为
()
A.4mB.-4mC.6mD.-6m
2.在有理数中,绝对值等于它本身的数有()
A.一个 B.无数个 C.三个 D.两个
3.|x|=1,则 x 与-3 的差为( )
A.4B.-2C.4 或 2D.2
4.与 a+b-c 的值相等的是( )
A.a-(-b)-(-c) B.a - ( - b) -
(+c)
C.a+(-b)-c D.a+(c-b)
5.如果一个整数加 4 为正,加 2 为负,那么
这个数与-2 的和为( )
A.-4 B.-5 C.5 D.4
6.下面等式错误的是( )
A.
2
1 -
3
1 -
5
1 =
2
1 -(
3
1 +
5
1 )
B.-5+2+4=4-(5+2)
C.(+3)-(-2)+(-1)=3+2-1
D.2-3-4=-(-2)-(+3)+(-4)
三、列式计算
1.负 50,正 13,正 12,负 11 的和是多少?
2.某水库正常水位是 15 米,二个月后水位
下降了 2 米,记作-2 米,第 3 个月时下了
一场大雨,使水位上升了 0.5 米,记作+0.5
米,求此时水位.
3.室内温度是 32℃,小明打开空调后,温度
下降了 6℃,记作-6℃,当关上空调后 1
小时,空气温度又回升了 2℃,记作+2℃,求
此时室内温度.
四、下表记录了初一(1)班一个组学生的
体重,平均体重是 50 kg.
姓名 小
明
小
丁
小
丽
小
文
小
天
小
乐
体重与标
准体重的
-
5 +3
-
7 +4 +6 0
差值
(1)谁最重?谁最轻?
(2)最重比最轻的重多少千克?
五、“学雷锋活动月”活动中,对某小组做
好事情况进行统计如下表
姓名 小
明
小
红
小
娟
小
青
好事件数 18 16
本人所做好事与人
均好事的差值 +3 0
-
4
(1)完成上表.
(2)谁做的好事最多,谁最少?
(3)最多的比最少的多多少?
一、填空题
1.0×(-m)=_______,m·0=_______.
2.( -
3
1 ) ×
7
3 =____,( -
16
3 ) × ( -
9
16 )=_____.
3.(-5)×(1+
5
1 )=_______,x·
x
1 =_______.
4.
8
7 ×(-
10
3 )×0×(
19
17 )=_______.
5.a>0,b<0,则 ab_______0.
6.|a+2|=1,则 a=_______.
7.几个不等于 0 的有理数相乘,它们的积的
符号如何确定_______.
8.(-2)×(-2)×(-2)×(-2)的积的符号是
__.
二、选择题
1.若 mn>0,则 m,n( )
A.都为正 B.都为负 C.同号 D.异号
2.已知 ab<|ab|,则有( )
A.ab<0B.a0,b<0D.a<00 C.mn≤0 D.mn
≥0
4.下列结论正确的是( )
A.-
3
1 ×3=1 B.| -
7
1 | ×
7
1 = -
49
1
C.-1 乘以一个数得到这个数的相反
数 D.几个有理数相乘,同号得正
三、在下图中填上适当的数
四、已知|a|=5,|b|=2,ab<0.
求:1.3a+2b 的值.
2.ab 的值.
解:1.∵|a|=5,∴a=_______
∵|b|=2,∴b=_______
∵ab<0,∴当 a=_______时,b=_______,
当 a=_______时,b=_______.
∴3a+2b=_______或 3a+2b=_______.
2.ab=_______
∴3a+2b 的值为_______,ab 的值为
_______.
五(1)(
24
13
4
3
6
7
12
11 )×(-48)
(2(-56)×(-32)+(-44)×32
六、在某地区,夏季高山上的温度从山脚
起每升高 100 米平均降低 0.8 ℃,已知山脚
的温度是 24 ℃,山顶的温度是 4 ℃,试求这
座山的高度.
七.上午 6 点水箱里的温度是 78℃,此后每
小时下降 4.5℃,求下午 2 点水箱内的温度.
2.1.1 参考答案
一、1.-8 0 2.10 km 3.-0.3 万元
4.-2 0 5.减少 5% 6.-3.8 吨
二、1.D 2.A 3.B
三、1.× 2.× 3.√ 4.√ 5.√
四、(1)早晨 6 点-3℃,中午 12 点 1℃,
下午4 点0℃,晚上12 点-9℃ (2)6° (3)1
°
五、广电网络 东方明珠 上菱电器
思考:比 0℃低
2.1.2 答案:
一、1.-1,-2,-3,-4,-5 2. 0
3.正分数 负分数 4.-155 米
5.-
2
1 ,-
3
2 ,-
4
3 6.-600 元
7.-350 万 8.700 -700 米
9.-6 元
二、10.B 11.D 12.D 13.C 14.A
三、15.略 16.略
17.向西走了 2 千米 18.分别是语文和外语
19.(1)总收入 130 万,总支出 35 万
(2)总收入+130 万,总支出-35 万
(3)95 万
2.2.1 参考答案
思考:1.0 2.正数 负数
3.1.5 -0.5 -3 3 -2
总结:原点 正方向 单位长度
一、填空 1.-0.01 2.0 3.0 4.±3 5.3
二、1.× 2.× 3.√ 4.√ 5.×
三、1.A 2.B 3.C 4.A
四、
2.2.2 答案
一、1. 0 左方 右方 2.A 点 3.近 4.
±2 相反数 5.A、B、C 6.3 7.0 8.<
> < < 9. 0
二、10.A 11.C 12.C 13.D 14.B
三、15.-4,-3,-2,-1,0,1,2 数
轴略 16.-3,-
2
1 ,0,2
2
1 数轴略 17.0
2.3.1 参考答案
±1;±2;
2
5 ;-
2
5 ;+4;-4;0;2;±
2;2;±
10
1 ;0;0;100;-100;100
思考:不可能
一、1.绝对值 2.-
7
6
7
6 -
3
1 -
3
1
2
1
-
2
1 3.±1 非负数 4.互为相反数
5.
5
1 或--
5
1 6.m≥1 m<1 x=±4
x=±
2
1
二、1.B 2.C 3.C 4.D 5.A
三、1.× 2.√ 3.×
四、1.(1)x=2y=-3 z=5
2、x>0 x<0
2.3.2 答案
一、1.相等 2.近 3.
3
2 4. 0 5.±5 相
反数 6.互为相反数 7.> 8.负数 9.-
7,-6,-5,-4,-310.-
3
2 ,0,
5
1 ,
|-
2
1 |,|-5.1| 11.0 12.0 0 0 13.<
> < < 14.-4 2.6 0 -8.3
二、15.D 16.B 17.C 18.B
三、19.不能.因为方向相反,“马很快,车
的质量很好,只能离目的地越来越远”.
20.甲同学分数最高,丁同学分数最低,
因为甲同学得分为正,且绝对值最大,所
以分数最高,最高分比最低分高 80 分.
21.-3.5,-1.5,|0|,|-2|,3
3
1 ,|-
3.5|
2.4 参考答案
一、1.m -m 0 2.8 -
6
5 3.0 4.7 或
35.-10℃+3℃
二、1.× 2.√ 3.√ 4.× 5.×
三、1.B 2.D 3.B 4.D
四、(1)
(2)2 km (3)11 km
五、表 1 第 3 行依次为:+4,-1,+1,-
5,+4,-1+4 -1 +1 -5 +4 -1
六年净胜球总计:2
思考:(1)符号不变,将绝对值相加.
(2)取绝对值较大的那个数的符号,
再将绝对值相减.
(3)还是它本身.
2.5 参考答案
一、1.1 -1 2 2.a (-b) 3.10 7 4.
-3 5.2
7
3 6.正数 负数 这个数
7、-7℃ +3℃ 8. 3
二、1.C 2.D 3.A 4、 D 5.D 6.D
7.A
三、1.× 2.× 3.× 4.√ 5.×
四、1、
2
1 2、57℃ 3、-
8
3 4.0 5、54
米
2.6 参考答案
一、1.10 2.-51 3.14 4.-79
二、1.-27 2.12 24 3.13 4.30
三、5
四、50×10+[1+3+(-4)+(-1)+2+(-5)+(-
3)+0+3+(-2)]=500+(-6)=494(千克)
五、1.+4-(-5)=9
2.20 × 6+ [ +3+( - 2)+( -
1)+(+4)+(+2)+(-5)]=120+(+1)=121
121>120 比计划多了 1 辆.
六、解:(1)原式=23-17+7-16
=23+7-17-16=30-33=-3
(2)原式=(
3
2 +
3
1 -1)+(-
5
1 )=-
5
1
(3) 原 式 =( - 26.54) - 18.54+ [ ( -
6.4)+6.4]=(-26.54)-18.54=-
45.08
(4)原式=(-4
8
7 )+5
2
1 +(-4
4
1 )-3
8
1
=(-4
8
7 -4
4
1 -3
8
1 )+5
2
1
=-12
4
1 +5
2
1 =-6
4
3
(5)原式=1-[(-1)+
7
3 -5+
7
4 ]+4
=1-[(-1+
7
4
7
3 )-5]+4
=1-(-5)+4=10
七 、 解 : 1000+1500+( - 1200)+1100+( -
1700)
=1000+1500-1200+1100-1700
=1000+1500+1100-1200-1700
=3600-2900=700(米)
因此,这时这架飞机离海平面 700 米.
八 、 解 : 2+3+( - 7.5)+( - 3)+5+( -
8)+3.5+4.5+8+( - 1.5)=2+3 - 7.5 - 3+5 -
8+3.5+4.5+8-1.5=2+5+3.5+4.5+3-3-8+8
-7.5-1.5=6.
因此,10 名学生的总体重为:
50×10+6=506(千克)
10 名学生的平均体重为:
506÷10=50.6(千克)
2.7 参考答案
一、1.-6 2.-1 3.2-5-3+1 4.-8 5.
-1 千米 6.(1)-6 (2)18 (3)28 (4)
-28 7.49 8.-4℃
二、1.C 2.B 3.C 4.B 5.B 6.B
三、1.-36 2.13.5(米) 3.28℃
四、(1)小天最重 小丽最轻 (2)13 kg
五.(1)小娟 15 小青 11 小红+1
(2)小明最多、小青最少
(3)7 件
2.8 参考答案
一、1.0 0 2.-
7
1
3
1 3.-6 1 4.0 5.
< 6.-1 或-3
7.当负数个数为偶数时,积为正数,当
负数个数为奇数时,积为负数. 8.正
二、1.C 2.A 3.C 4.C
三、
四、1.±5 ±2 5 -2 -5 2 11 -
112.±10 ±11 -10
五、略
六、解:根据题意,得这座山的高度为:
100 × [ (24 - 4) ÷ 0.8 ] =100 ×
25=2500(米)
七、解:下午 2 点即为 14 点
78-4.5×(14-6)=78-36=42(℃)
因此,下午 2 时水箱内的温度是 42℃.