旋转对称图形教案2

旋转对称图形教案2

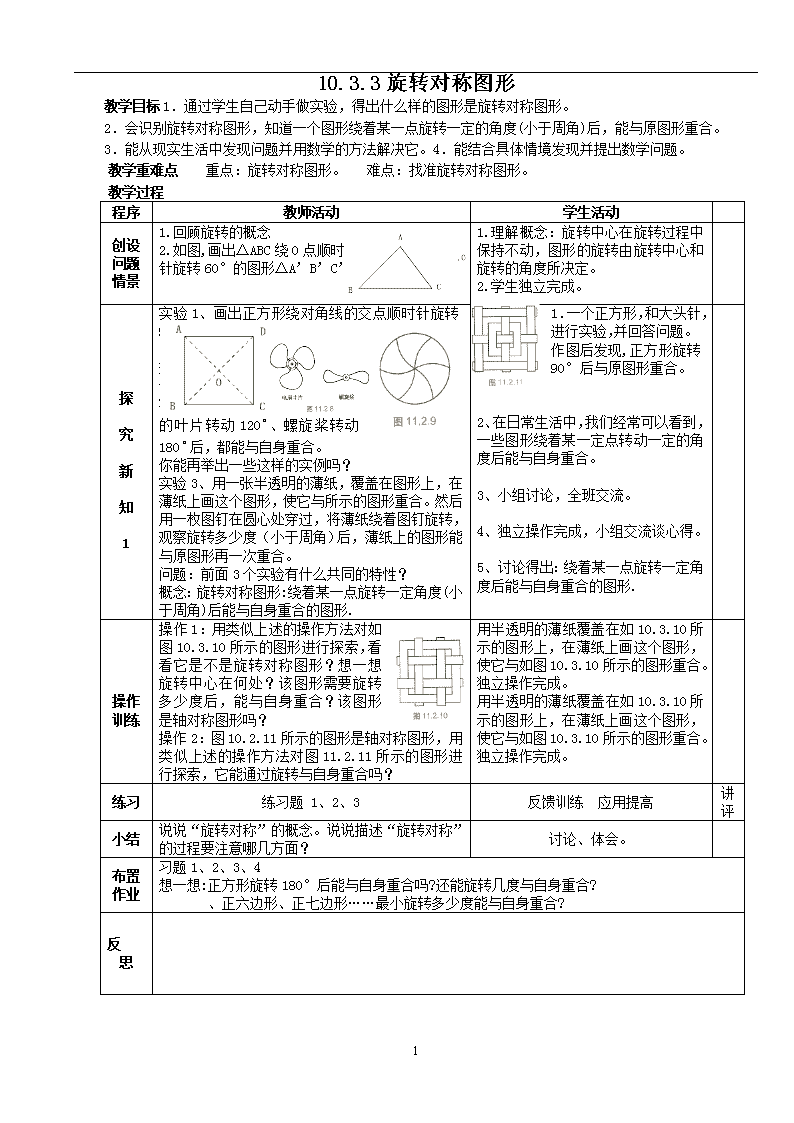
‎ ‎ ‎10.3.3旋转对称图形 ‎ 教学目标1．通过学生自己动手做实验，得出什么样的图形是旋转对称图形。‎ ‎ 2．会识别旋转对称图形，知道一个图形绕着某一点旋转一定的角度(小于周角)后，能与原图形重合。‎ ‎ 3．能从现实生活中发现问题并用数学的方法解决它。4．能结合具体情境发现并提出数学问题。‎ 教学重难点 重点：旋转对称图形。 难点：找准旋转对称图形。‎ 教学过程 程序 教师活动 学生活动 创设 问题 情景 ‎1.回顾旋转的概念 ‎2.如图,画出ΔABC绕O点顺时 针旋转60°的图形ΔA’B’C’. ‎ ‎1.理解概念：旋转中心在旋转过程中保持不动，图形的旋转由旋转中心和旋转的角度所决定。‎ ‎2.学生独立完成。‎ 探 究 新 知 ‎1‎ 实验1、画出正方形绕对角线的交点顺时针旋转90°的图形.‎ 观察旋转后的图形与原正方形有何关系?‎ 实验2．如图11.2.8所示，电扇的叶片转动120、螺旋桨转动180后，都能与自身重合。‎ 你能再举出一些这样的实例吗？‎ 实验3、用一张半透明的薄纸，覆盖在图形上，在薄纸上画这个图形，使它与所示的图形重合。然后用一枚图钉在圆心处穿过，将薄纸绕着图钉旋转，观察旋转多少度（小于周角）后，薄纸上的图形能与原图形再一次重合。‎ 问题：前面3个实验有什么共同的特性？‎ 概念：旋转对称图形:绕着某一点旋转一定角度(小于周角)后能与自身重合的图形.‎ ‎1．一个正方形，和大头针，进行实验，并回答问题。‎ 作图后发现,正方形旋转90°后与原图形重合。‎ ‎2、在日常生活中，我们经常可以看到，一些图形绕着某一定点转动一定的角度后能与自身重合。‎ ‎3、小组讨论，全班交流。‎ ‎4、独立操作完成，小组交流谈心得。‎ ‎5、讨论得出：绕着某一点旋转一定角度后能与自身重合的图形.‎ 操作 训练 操作1：用类似上述的操作方法对如图10.3.10所示的图形进行探索，看看它是不是旋转对称图形？想一想旋转中心在何处？该图形需要旋转多少度后，能与自身重合？该图形是轴对称图形吗？‎ 操作2：图10.2.11所示的图形是轴对称图形，用类似上述的操作方法对图11.2.11所示的图形进行探索，它能通过旋转与自身重合吗？‎ 用半透明的薄纸覆盖在如10.3.10所示的图形上，在薄纸上画这个图形，使它与如图10.3.10所示的图形重合。独立操作完成。‎ 用半透明的薄纸覆盖在如10.3.10所示的图形上，在薄纸上画这个图形，使它与如图10.3.10所示的图形重合。独立操作完成。‎ 练习 练习题 1、2、3‎ 反馈训练 应用提高 讲评 小结 说说“旋转对称”的概念。说说描述“旋转对称”的过程要注意哪几方面？‎ 讨论、体会。‎ 布置 作业 习题1、2、3、4‎ 想一想:正方形旋转180°后能与自身重合吗?还能旋转几度与自身重合?‎ ‎ 、正六边形、正七边形……最小旋转多少度能与自身重合?‎ 反 思 2‎ ‎ ‎ 2‎