沪科版七年级数学上册第五章测试题（含答案）

沪科版七年级数学上册第五章测试题（含答案）

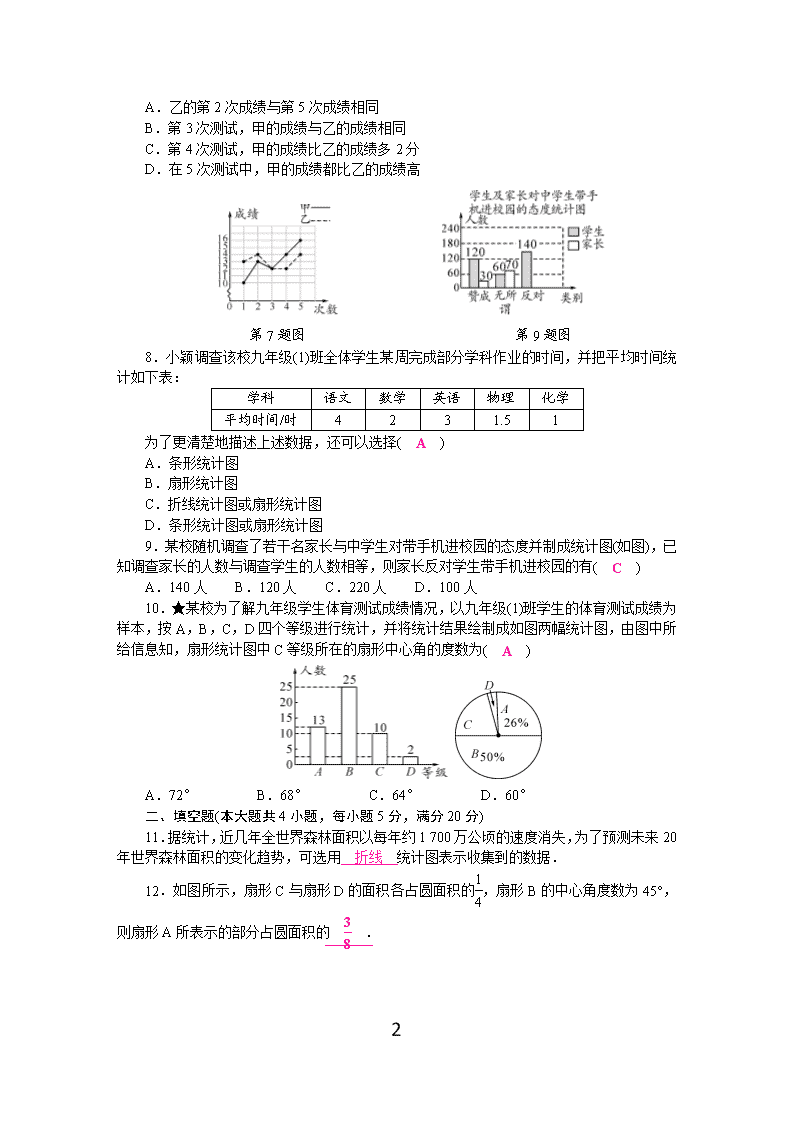
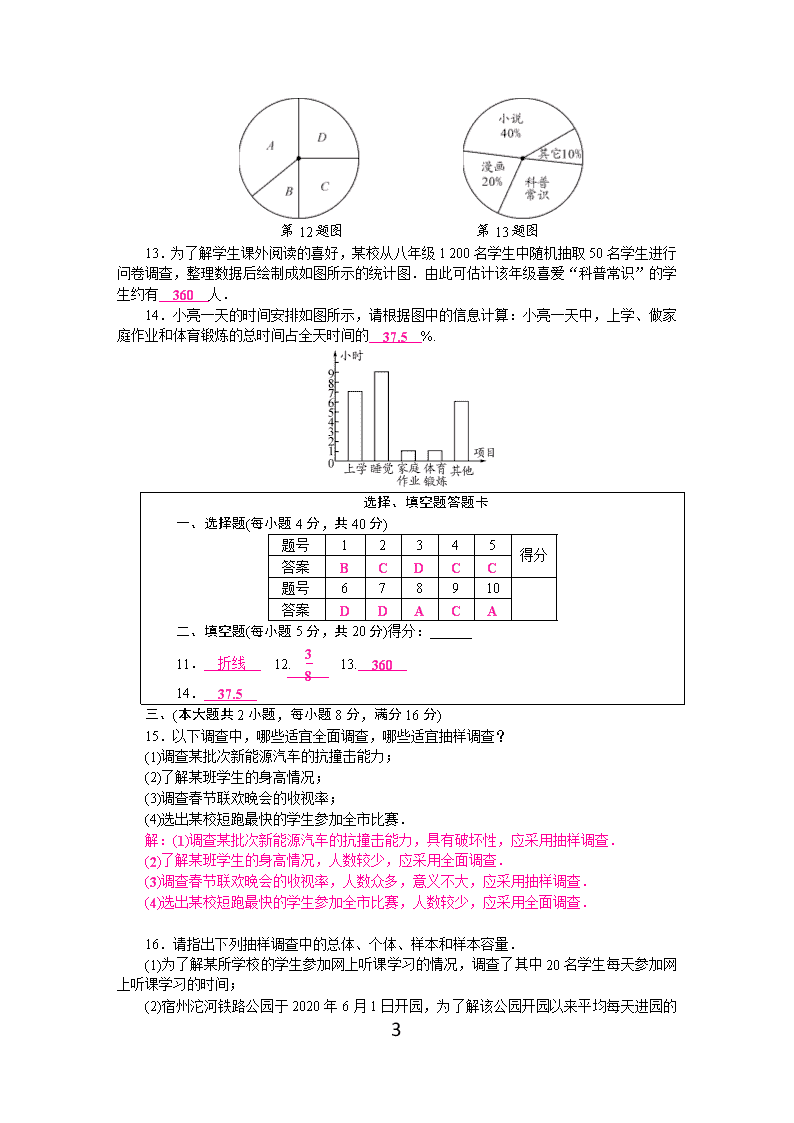
沪科版七年级数学上册第五章测试题（含答案）‎ ‎(考试时间：120分钟　　　满分：150分)‎ 分数：____________‎ 7‎ 一、选择题(本大题共10小题，每小题4分，满分40分)‎ 每小题都给出A、B、C、D四个选项，其中只有一个是正确的．‎ ‎1．下列调查统计中，适合采用普查方式的是(　B　)‎ A．华为手机的市场占有率 B．疫情防控期间，乘坐飞机的旅客体温是否正常 C．“国家宝藏”专栏电视节目的收视率 D．“现代”汽车每百公里的耗油量 ‎2．为了解一批电视机的使用寿命，从中抽取100台电视机进行试验，这个问题的样本是(　C　)‎ A．这批电视机 B．这批电视机的使用寿命 C．抽取的100台电视机的使用寿命 D．100台 ‎3．为了解2020年巢湖市九年级7 731名学生的实验操作考试成绩，如果按10%的比例进行抽样调查，在这个问题中，有下列说法：①这7 731名学生是总体；②每个学生是个体；③7 731名学生的实验操作考试成绩是总体的一个样本；④样本容量是10%.其中正确的有(　D　)‎ A．4个 B．3个 C．2个 D．1个 ‎4．谢老师对班上某次数学模拟考试成绩进行统计，绘制了如图所示的统计图，根据图中给出的信息，这次考试成绩达到A等级的人数占总人数的(　C　)‎ A．6% B．10% C．20% D．25%‎ ‎ ‎ 第4题图　 第5题图 ‎5．某校为调查1 000名学生对新闻、娱乐、动画、体育四类电视节目的喜爱情况，随机抽取了部分学生进行调查，并利用调查数据作出如图所示的扇形统计图．根据图中信息，可以估算出该校喜爱体育节目的学生共有(　C　)‎ A．300名 B．250名 C．200名 D．150名 ‎6．某课外兴趣小组为了解所在地区的老年人的健康状况，分别作了四种不同的抽样调查，你认为抽样较合理的是(　D　)‎ A．在公园调查了1 000名老年人的健康状况 B．在医院调查了1 000名老年人的健康状况 C．调查了100名小区内老年邻居的健康状况 D．利用派出所的户籍网随机调查了该地区10%的老年人的健康状况 ‎7．甲，乙两人参加某体育项目训练，为了便于研究，把最后5次的训练成绩分别用实线和虚线连接起来，如图，下面的结论中错误的是(　D　)‎ 7‎ A．乙的第2次成绩与第5次成绩相同 B．第3次测试，甲的成绩与乙的成绩相同 C．第4次测试，甲的成绩比乙的成绩多2分 D．在5次测试中，甲的成绩都比乙的成绩高 ‎ ‎ 第7题图 　第9题图 ‎8．小颖调查该校九年级(1)班全体学生某周完成部分学科作业的时间，并把平均时间统计如下表：‎ 学科 语文 数学 英语 物理 化学 平均时间/时 ‎4‎ ‎2‎ ‎3‎ ‎1.5‎ ‎1‎ 为了更清楚地描述上述数据，还可以选择(　A　)‎ A．条形统计图 B．扇形统计图 C．折线统计图或扇形统计图 D．条形统计图或扇形统计图 ‎9．某校随机调查了若干名家长与中学生对带手机进校园的态度并制成统计图(如图)，已知调查家长的人数与调查学生的人数相等，则家长反对学生带手机进校园的有(　C　)‎ A．140人 B．120人 C．220人 D．100人 ‎10．★某校为了解九年级学生体育测试成绩情况，以九年级(1)班学生的体育测试成绩为样本，按A，B，C，D四个等级进行统计，并将统计结果绘制成如图两幅统计图，由图中所给信息知，扇形统计图中C等级所在的扇形中心角的度数为(　A　)‎ ‎ ‎ A．72° B．68° C．64° D．60°‎ 二、填空题(本大题共4小题，每小题5分，满分20分)‎ ‎11．据统计，近几年全世界森林面积以每年约1 700万公顷的速度消失，为了预测未来20年世界森林面积的变化趋势，可选用 折线 统计图表示收集到的数据．‎ ‎12．如图所示，扇形C与扇形D的面积各占圆面积的，扇形B的中心角度数为45°，则扇形A所表示的部分占圆面积的 ．‎ 7‎ ‎ ‎ 第12题图　　 第13题图 ‎13．为了解学生课外阅读的喜好，某校从八年级1 200名学生中随机抽取50名学生进行问卷调查，整理数据后绘制成如图所示的统计图．由此可估计该年级喜爱“科普常识”的学生约有 360 人．‎ ‎14．小亮一天的时间安排如图所示，请根据图中的信息计算：小亮一天中，上学、做家庭作业和体育锻炼的总时间占全天时间的 37.5 %.‎ 选择、填空题答题卡 一、选择题(每小题4分，共40分)‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 得分 答案 B C D C C 题号 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ 答案 D D A C A 二、填空题(每小题5分，共20分)得分：______‎ ‎11． 折线 　12. 　13. 360 ‎ ‎14． 37.5 ‎ 三、(本大题共2小题，每小题8分，满分16分)‎ ‎15．以下调查中，哪些适宜全面调查，哪些适宜抽样调查？‎ ‎(1)调查某批次新能源汽车的抗撞击能力；‎ ‎(2)了解某班学生的身高情况；‎ ‎(3)调查春节联欢晚会的收视率；‎ ‎(4)选出某校短跑最快的学生参加全市比赛．‎ 解：(1)调查某批次新能源汽车的抗撞击能力，具有破坏性，应采用抽样调查．‎ ‎(2)了解某班学生的身高情况，人数较少，应采用全面调查．‎ ‎(3)调查春节联欢晚会的收视率，人数众多，意义不大，应采用抽样调查．‎ ‎(4)选出某校短跑最快的学生参加全市比赛，人数较少，应采用全面调查．‎ ‎16．请指出下列抽样调查中的总体、个体、样本和样本容量．‎ ‎(1)为了解某所学校的学生参加网上听课学习的情况，调查了其中20名学生每天参加网上听课学习的时间；‎ ‎(2)宿州沱河铁路公园于2020年6月1日开园，为 7‎ 了解该公园开园以来平均每天进园的人数，对其中30天进园的人数进行了统计．‎ 解：(1)总体是某所学校的学生参加网上听课学习的情况，个体是每名学生每天参加网上听课学习的时间；‎ 样本是抽查的20名学生每天参加网上听课学习的时间；样本容量是20.‎ ‎(2)总体是沱河铁路公园开园以来平均每天进园的人数，个体是沱河铁路公园开园以来每天进园的人数，样本是沱河铁路公园开园以来其中30天进园的人数，样本容量是30.‎ 四、(本大题共2小题，每小题8分，满分16分)‎ ‎17．小明家有一养鸡场，为了估计一下今年鸡的只数，从中捕获50只做上记号，放回后3天，又捕获100只，见到有记号的鸡3只，再放回后第3天，又捕获100只，见到有记号的鸡4只．请你估计一下小明家的鸡场有多少只鸡？‎ 解：设小明家有鸡x只，根据题意，得 ‎50 ∶x＝(3＋4) ∶(100＋100)，‎ 解得x＝1 428.57≈1 429，‎ ‎∴估计小明家的鸡场有1 429只鸡．‎ ‎18．植树节，杜老师带同学们去植树，第1行植了50棵，第2行植了42棵，第3行植了36棵，第4行植了30棵，第5行植了27棵，第6行植了25棵，用表格表示上面的数据，并从数据中看出植树的棵数是怎样随行的变化而变化的．‎ 解：植树统计表：‎ 行数 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 棵树 ‎50‎ ‎42‎ ‎36‎ ‎30‎ ‎27‎ ‎25‎ 从数据中看出植树的棵数随行数的增加而减少．‎ 五、(本大题共2小题，每小题10分，满分20分)‎ ‎19．某校计划成立学生社团，要求每一位学生都选择一个社团，为了解学生对不同社团的喜爱情况，学校随机抽取了部分学生进行“我最喜爱的一个学生社团”问卷调查，规定每人必须并且只能在“文学社团”、“科技社团”、“书画社团”、“体育社团”和“其他”五项中选择一项，并将统计结果绘制成了如下两个不完整的统计图表．‎ 社团名称 文学社团 科技社团 书画社团 体育社团 其他 人数 ‎18‎ a ‎45‎ ‎72‎ b 请解答下列问题：‎ ‎(1)a＝ 36 ，b＝ 9 ；‎ ‎(2)在扇形统计图中，“书画社团”所对应的扇形的中心角度数为 90° ；‎ ‎(3)若该校共有3 000名学生，试估计该校学生中选择“文学社团”的人数．‎ 解：估计该校学生中选择“文学社团”的人数是 7‎ ‎3 000×＝300(人).‎ ‎20．“校园安全”受到全社会的广泛关注，某校政教处对部分学生及家长就校园安全知识的了解程度进行了随机抽样调查，并绘制成如图所示的两幅统计图，请根据统计图中的信息，解答下列问题：‎ ‎(1)参与调查的学生及家长共有 400 人；‎ ‎(2)在扇形统计图中，“基本了解”所对应的圆心角的度数是 135 度；‎ ‎(3)在条形统计图中，“非常了解”所对应的学生人数是 83 人；‎ ‎(4)若全校有1 200名学生，请你估计对“校园安全”知识达到“非常了解”和“基本了解”的学生共有多少人？‎ ‎ ‎ 解：调查的学生的总人数是 ‎83＋77＋31＋4＝195(人).‎ 对“校园安全”知识达到“非常了解”和“基本了解”的学生是83＋77＝160(人)，‎ 则全校有1 200名学生中，达到“非常了解”和“基本了解”的学生是1 200×≈985(人).‎ 答：达到“非常了解”和“基本了解”的学生共有985人．‎ 六、(本题满分12分)‎ ‎21．某校有三个年级，各年级的人数分别为七年级600人，八年级540人，九年级565人，学校为了解学生生活习惯是否符合低碳观念，在全校进行了一次问卷调查，若学生生活习惯符合低碳观念，则称其为“低碳族”；否则称其为“非低碳族”，经过统计，将全校的低碳族人数按照年级绘制成如下两幅统计图：‎ ‎ ‎ ‎① ②‎ ‎(1)根据图①、图②，计算八年级“低碳族”人数，并补全上面两个统计图；‎ ‎(2)小丽依据图①、图②提供的信息通过计算认为，与其他两个年级相比，九年级的“低碳族”人数在本年级全体学生中所占的比例较大，你认为小丽的判断正确吗？说明理由．‎ 解：(1)由题意可知，全校“低碳族”人数为 ‎300÷25%＝1 200(人)，‎ 7‎ 八年级“低碳族”人数为1 200×37%＝444(人)，‎ 九年级“低碳族”人数占全校“低碳族”人数的百分比＝1－25%－37%＝38%．‎ 补全的统计图如图①、图②所示．‎ ‎(2)小丽的判断不正确，‎ 理由：‎ 七年级“低碳族”人数占该年级人数的百分比＝×100%＝50%，‎ 八年级“低碳族”人数占该年级人数的百分比＝＝×100%≈82.2%，‎ 九年级“低碳族”人数占该年级人数的百分比＝×100%≈80.7%，‎ ‎∵50%<80.7%<82.2%，‎ ‎∴小丽的判断不正确，八年级的学生中，“低碳族”人数比例较大．‎ 七、(本题满分12分)‎ ‎22．为了参加学校举行的传统文化知识竞赛，某班进行了四次模拟训练，将成绩优秀的人数和优秀率绘制成如下两幅不完整的统计图：‎ 请根据以下两图解答下列问题：‎ ‎ ‎ ‎(1)该班总人数是 40 ；‎ ‎(2)根据计算，请你补全两幅统计图；‎ ‎(3)观察补全后的统计图，写出一条你发现的结论.‎ 解：(2)由(1)得，第四次优秀的人数为 ‎40×85%＝34(人)；‎ 第三次优秀率为×100%＝80%；‎ 补全两幅统计图如图所示．‎ ‎(3)答案不唯一，如优秀人数逐渐增多，增大的幅度逐渐减小等．‎ 八、(本题满分14分)‎ ‎23．“你记得父母的生日吗？”这是某校在九年级学生中开展主题为“感恩”教育时设置的一个问题，有以下四个选项：A.父母生日都记得；B.只记得母亲生日；C.只记得父亲生日；D.父母生日都不记得．在随机调查了(1)班和(2)班各50名学生后，根据相关数据绘出如图所示的统计图．‎ ‎(1)补全频数分布直方图；‎ ‎(2)据此推算，九年级共900名学生中，“父母生日都不记得”的学生共多少名？‎ ‎(3)若两个班中“只记得母亲生日”的学生占22%，则(2)班“只记得母亲生日”‎ 7‎ 的学生所占百分比是多少？‎ ‎　‎ 解：(1)一班中A类的人数是 ‎50－9－3－20＝18(人).‎ 补全频数分布直方图如图所示．‎ ‎(2)×900＝351(名).‎ 即“父母生日都不记得”的学生共351名．‎ ‎(3)设(2)班“只记得母亲生日”的学生有x名，依题意，得 ×100%＝22%，‎ 解得x＝13，∴×100%＝26%，‎ 即(2)班“只记得母亲生日”的学生所占百分比是26%．‎ 7‎