- 2021-10-22 发布 |
- 37.5 KB |
- 28页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
七年级下册数学课件《探索直线平行的条件 利用内错角同旁内角判断两直线平行》 (2)_北师大版
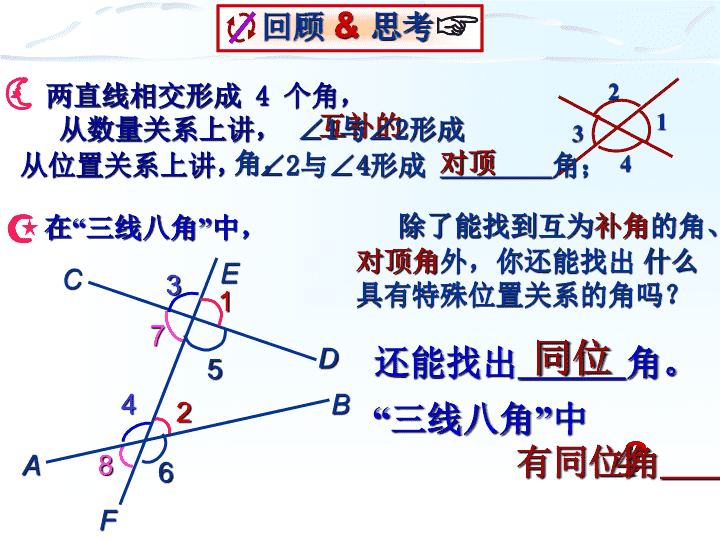
回顾与思考 A C B D E F 12 3 4 56 7 8 活动1 观察∠3与∠5的位置关系: ①在截线EF的两侧 ②在被截直线AB、CD的内部 3 5 ∠4和∠6图中的内错角还有哪些? 内错角 讲授新课 内错角、同旁内角的概念一 变式图形:图中的∠1与∠2都是内错角. 图形特征:在形如“Z”的图形中有内错角. 1 2 1 1 12 2 2 A C B D E F 12 3 4 56 7 8 活动2 观察∠4与∠5的位置关系 ①在截线EF的同旁 ②在被截直线AB、CD的内部 4 5 ∠3和∠6图中还有哪些同旁内角? 同旁内角 变式图形:图中的∠1与∠2都是同旁内角. 图形特征:在形如“U”的图形中有同旁内角. 1 1 1 1 2 2 2 2 例1 如图,直线DE截AB ,AC,构成8个角,指出所 有的同位角,内错角,同旁内角. 解:两条直线是AB,AC,截线是DE ,所以8个角中, 同位角:∠2与∠5,∠4与∠7, ∠1与∠8, ∠6和∠3; 内错角:∠4与∠5,∠1与∠6; 同旁内角:∠1与∠5,∠4与∠6. 变式:∠A与∠8是哪两条直线被第哪条直线所截的角 ?它们是什么关系的角?∠A与∠5呢?∠A与∠6呢? ED CB A 8 76 5 43 2 1 典例精析 例2 如图,直线DE,BC被直线AB所截. (1)∠1与∠2, ∠1和∠3,∠1和∠4各是什么角? 4 32 1 F ED CB A解:∠1与∠2是内错角, ∠1和∠3同旁内角, ∠1和∠4是同位角. 注意:解题之前要明确哪两条直线被哪条直线所截. 解:∵∠1=∠4,∠2=∠4, ∴∠1=∠2 ∵∠3和∠4互补 即∠4+∠3=180° 又∵∠1=∠4 ∴∠1+∠3=180° 即∠1与∠3互补 4 32 1 F ED CB A (2)如果∠1=∠4,那么∠1与∠2相等吗?∠1 与∠3互补吗?为什么? 问题1 两条直线被第三条直线所截,同时得到同位 角、内错角和同旁内角,由同位角相等可以判定两 直线平行,那么,能否利用内错角和同旁内角来判 定两直线平行呢? 如图,由3=2,可推出a//b吗?如何推出? 解: ∵ 1=3(对顶角相等), 3=2(已知), 1=2. a//b(同位角相等,两直线平行). 2 b a1 3 利用内错角、同旁内角判定两条直线平行二 判定方法2:两条直线被第三条直线所截 ,如果内 错角相等,那么这两条直线平行. 简单说成:内错角相等,两直线平行. 2 b a1 3 ∵∠3=∠2(已知) ∴a∥b(内错角相等,两直线平行) 应用格式: 总结归纳 问题2 如图,如果1+2=180° ,你能判定a//b吗? c 解:能, ∵1+2=180°(已知) 1+3=180°(邻补角定义) 2=3(同角的补角相等) a//b(同位角相等,两直线平行) 2 b a 1 3 判定方法3:两条直线被第三条直线所截 ,如果同 旁内角互补,那么这两条直线平行. 简单说成:同旁内角互补,两直线平行. 应用格式: 2 b a 1 3 ∵∠1+∠2=180°(已知) ∴a∥b(同旁内角互补,两直线平行) 总结归纳 1.如图,∠1=30°,∠2或∠3满足条件 ___________________,则a//b. 2 1 3 a b c ∠2=150°或∠3=30° 当堂练习 2.如图.(1)从∠1=∠4,可以推出 ∥ , 理由是 . (2)从∠ABC +∠ =180°,可以推出AB∥CD , 理由是 . A B C D 1 2 3 4 5 AB 内错角相等,两直线平行 CD BCD 同旁内角互补,两直线平行 3.如图,已知∠1= ∠3,AC平分∠DAB你能判断 那两条直线平行?请说明理由? 2 3 A B CD )) 1 (解: AB∥CD. 理由: ∵AC平分∠DAB(已知) ∴∠1=∠2(角平分线定义) 又∵∠1=∠3(已知) ∴∠2=∠3(等量代换) ∴AB∥CD( 内错角相等,两直线平行) 1.同位角、内错角、同旁内角的结构特征: 三线八角 同位角 “F”型 内错角 “Z”型 同旁内角 “U”型 2. 在图形中判断三线八角的方法:描图法: ①把两个 角在图中描画出来;②找到两个角的公共直线;③观 察所描的角,判断所属“字母”类型,同 位角为“F” 型,内错角为“Z”型,同旁内角为“U”型,注意图形 的变式(旋转、对称)也是符合的. 课堂小结 判定两条直线平行的方法 同位角 内错角 同旁内角 ∠1=∠2 ∠3=∠2 ∠2+∠4=180° a b c 1 2 43 文字叙述 符号语言 图形 相等 两直线平行 ∵ (已知) ∴a∥b ________相等 两直线平行 ∵ (已知) ∴a∥b _________互补 两直线平行 ∵ (已知) ∴a∥b 内错角相等,两直线平行. 同旁内角互补,两直线平行. 做一做做一做 随堂练习 作业查看更多