- 2021-10-22 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
华师大版七年级数学上册期末测试题(含答案)
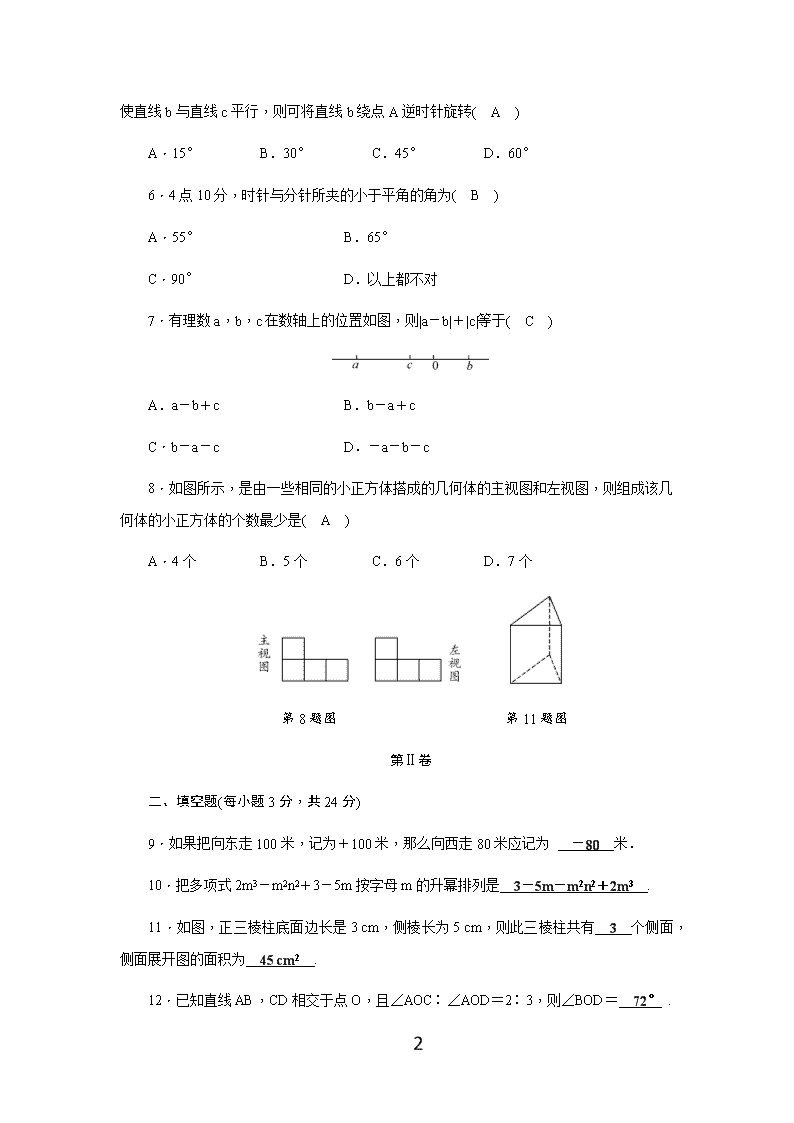
华师大版七年级数学上册期末测试题(含答案) (考试时间:120分钟 满分:120分) 第Ⅰ卷 一、选择题(每小题3分,共24分) 1.今年国庆黄金周期间,四川全省旅游总收入为52 471 000 000元.用科学记数法表示52 471 000 000为( A ) A.5.247 1×1010 B.5.247 1×109 C.52.471×109 D.0.524 71×1011 2.下列说法正确的是( C ) A.-5不是单项式 B.2a2+-5是二次三项式 C.x2-2x+3是二次三项式 D.-2a2b的系数是3 3.如图所示,下列结论中正确的是( B ) A.∠1和∠2是同位角 B.∠2和∠3是同旁内角 C.∠1和∠4是内错角 D.∠3和∠4是对顶角 第3题图 第5题图 4.下列各组数中,相等的是( C ) A.(-5)2和-52 B.|-5|2和-52 C.(-7)3与-73 D.|-7|3与-73 5.如图,直线a与直线b交于点A,与直线c交于点B,∠1=120°,∠2=45°, 7 若使直线b与直线c平行,则可将直线b绕点A逆时针旋转( A ) A.15° B.30° C.45° D.60° 6.4点10分,时针与分针所夹的小于平角的角为( B ) A.55° B.65° C.90° D.以上都不对 7.有理数a,b,c在数轴上的位置如图,则|a-b|+|c|等于( C ) A.a-b+c B.b-a+c C.b-a-c D.-a-b-c 8.如图所示,是由一些相同的小正方体搭成的几何体的主视图和左视图,则组成该几何体的小正方体的个数最少是( A ) A.4个 B.5个 C.6个 D.7个 第8题图 第11题图 第Ⅱ卷 二、填空题(每小题3分,共24分) 9.如果把向东走100米,记为+100米,那么向西走80米应记为 -80 米. 10.把多项式2m3-m2n2+3-5m按字母m的升幂排列是 3-5m-m2n2+2m3 . 11.如图,正三棱柱底面边长是3 cm,侧棱长为5 cm,则此三棱柱共有 3 个侧面,侧面展开图的面积为 45 cm2 . 12.已知直线AB,CD相交于点O,且∠AOC∶∠AOD=2∶3,则∠BOD= 72° . 7 13.两个角的度数之比为6∶4,它们的差为36°,则这两个角的关系是 互补 . 14.定义一种新运算“*”:x*y=2xy-x2,如3*4=2×3×4-32=15,则2*(-1*2)= -24 . 15.若a,b互为相反数,c,d互为倒数,m的绝对值是2,则2m-2 019(a+b)-cd的值是 3或-5 . 16.(十堰中考)当x=1时,ax+b+1的值为-2,则(a+b-1)(1-a-b)的值为 -16 . 三、解答题(要求写出必要的解题过程;共8题,17题-24题每题9分,共72分) 17.计算下列各式: (1)(-2)2×5-(-2)3÷4; 解:原式=4×5-(-8)÷4 =22. (2)-32×+×(-24). 解:原式=-9×-18-4-9 =-32. 18.化简: (1)3(a2b-ab2)-2(6a2b+ab2); 解:原式=3a2b-3ab2-12a2b-2ab2 =-9a2b-5ab2. (2)3x2-[8x-2(5x-4)-2x2]. 7 解:原式=3x2-(8x-10x+8-2x2)=3x2-(-2x+8-2x2)=3x2+x-4+x2=4x2+x-4. 19.先化简,再求值:5(3a2b-ab2-1)-(ab2+3a2b-5).其中a=-,b=. 解:原式=15a2b-5ab2-5-ab2-3a2b+5=12a2b-6ab2. 当a=-,b=时,原式=12××-6×·= . 20.如图,B,C两点把线段AD分成2∶4∶3的三部分,点M是AD的中点,CD=6,求线段MC的长. 解:设AB=2x,则BC=4x,CD=3x,所以AD=2x+4x+3x=9x,因为CD=6,即3x=6,所以x=2,所以AD=9x=18,又因为点M为AD的中点,所以MD=AD=×18=9,所以MC=MD-CD=9-6=3. 21.a表示十位上的数,b表示个位上的数. (1)用代数式表示这个两位数; (2)把这个两位数的十位上的数与个位上的数交换位置,计算所得的数与原数的和; (3)这个和能被11整除吗?若能,请说明理由;若不能,请举一个例子. 解:(1)10a+b. 7 (2)交换位置后所得的数为10b+a,所以(10a+b)+(10b+a)=11a+11b. (3)能,因为11a+11b=11(a+b)且11(a+b)÷11=a+b(a,b为正整数), 所以11a+11b被11整除. 22.某市某公交车从起点到终点共有六个站,一辆公交车由起点开往终点,在起点站始发时上了部分乘客,从第二站开始下车、上车的乘客数如表: 站次人数 二 三 四 五 六 下车(人) 3 6 10 7 19 上车(人) 12 10 9 4 0 (1)求本趟公交车在起点站上车的人数; (2)若公交车的收费标准是上车每人2元,计算此趟公交车从起点到终点的总收入. 解:(1)19-[(12-3)+(10-6)+(9-10)+(4-7)]=19-[9+4-1-3]=19-9=10 答:本趟公交车在起点站上车的人数是10人. (2)由(1)知起点上车10人, (10+12+10+9+4)×2=45×2=90(元). 答:此趟公交车从起点到终点的总收入是90元. 7 23.如图,已知∠HDC+∠ABC=180°,∠HFD=∠BEG,∠H=20°,求∠G的度数. 解:因为∠BEG=∠AEF,∠HFD=∠BEG,所以∠HFD=∠AEF.所以DC∥AB.所以∠HDC=∠DAB.因为∠HDC+∠ABC=180°,所以∠DAB+∠ABC=180°.所以AD∥BC.所以∠H=∠G.因为∠H=20°,所以∠G=20°. 24.如图,点O为直线AB上一点,过点O作射线OC,使∠BOC=110°.将一直角三角板的直角顶点放在点O处(∠OMN=30°),一边OM在射线OB上,另一边ON在直线AB的下方. (1)求图①中的三角板绕点O逆时针旋转至图②,使一边OM在∠BOC的内部,且恰好平分∠BOC,求∠BON的度数. (2)将图①中的三角板绕点O以每秒5°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为 11或47 .(直接写出结果). (3)将图①中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,请探究∠AOM与∠NOC的数量关系,并说明理由. 解:(1)如图②,因为OM平分∠BOC,所以∠MOC=∠MOB=∠BOC.又因为∠ 7 BOC=110°,所以∠MOB=55°, 因为∠MON=90°,所以∠BON=∠MON-∠MOB=35°; (2)分两种情况: ①如图②,因为∠BOC=110°,所以∠AOC=70°, 当直线ON恰好平分锐角∠AOC时,∠AOD=∠COD=35°, 所以∠BON=35°,∠BOM=55°, 即逆时针旋转的角度为55°, 由题意得5t=55°,解得t=11(s); ②如图③,当NO平分∠AOC时,∠NOA=35°,所以∠AOM=55°, 即逆时针旋转的角度为:180°+55°=235°, 由题意得5t=235°,解得t=47(s), 综上所述,t=11s或47s时,直线ON恰好平分锐角∠AOC; 故答案为:11或47; (3)∠AOM-∠NOC=20°.理由如下: 因为∠MON=90°,∠AOC=70°,所以∠AOM=90°-∠AON,∠NOC=70°-∠AON, 所以∠AOM-∠NOC=(90°-∠AON)-(70°-∠AON)=20°, 所以∠AOM与∠NOC的数量关系为∠AOM-∠NOC=20°. 7查看更多