七年级下数学课件10-5 角平分线_鲁教版

七年级下数学课件10-5 角平分线_鲁教版

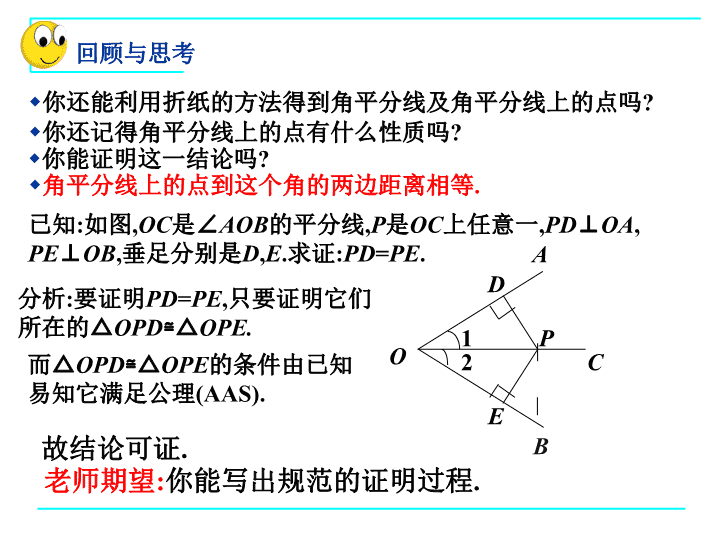
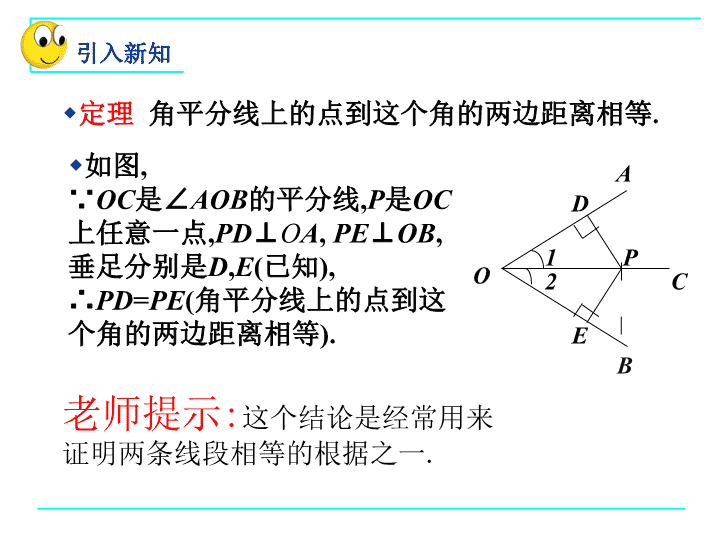
10.5角平分线（1） 你还能利用折纸的方法得到角平分线及角平分线上的点吗?已知:如图,OC是∠AOB的平分线,P是OC上任意一,PD⊥OA,PE⊥OB,垂足分别是D,E.求证:PD=PE.而△OPD≌△OPE的条件由已知易知它满足公理(AAS).故结论可证.老师期望:你能写出规范的证明过程.分析:要证明PD=PE,只要证明它们所在的△OPD≌△OPE.你还记得角平分线上的点有什么性质吗?角平分线上的点到这个角的两边距离相等.你能证明这一结论吗?OCB1A2PDE回顾与思考 定理角平分线上的点到这个角的两边距离相等.老师提示:这个结论是经常用来证明两条线段相等的根据之一.如图,∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴PD=PE(角平分线上的点到这个角的两边距离相等).OCB1A2PDE引入新知 你能写出“定理角平分线上的点到这个角的两边距离相等”的逆命题吗?逆命题在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.它是真命题吗?如果是.请你证明它.已知:如图,PD=PE,PD⊥OA,PE⊥OB,垂足分别是D,E.求证:点P在∠AOB的平分线上.分析:要证明点P在∠AOB的平分线上,可以先作出过点P的射线OC,然后证明∠1=∠2.老师期望:你能写出规范的证明过程.OCB1A2PDE引入新知 逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.如图,∵PA=PB,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).老师提示:这个结论又是经常用来证明点在直线上(或直线经过某一点)的根据之一.从这个结果出发,你还能联想到什么?OBAC12PDE动手练一练 已知:∠AOB,如图.求作:射线OC,使∠AOC=∠BOC.作法:用尺规作角的平分线.1.在OAT和OB上分别截取OD,OE,使OD=OE.2.分别以点D和E为圆心,以大于DE/2长为半径作弧,两弧在∠AOB内交于点C.3.作射线OC.请你说明OC为什么是∠AOB的平分线,并与同伴进行交流.老师提示:作角平分线是最基本的尺规作图,这种方法要确实掌握.ABOC则射线OC就是∠AOB的平分线.DE做一做 1.如图,AD,AE分别是△ABC中∠A的内角平分线和外角平分线,它们有什么关系?老师期望:你能说出结论并能证明它.EDABCF课内练习 2.如图,一目标在A区,到公路,铁路距离相等,离公路与铁路的交叉处500m.在图上标出它的位置(比例尺为1:20000).A区课内练习 定理角平分线上的点到这个角的两边距离相等.∵OC是∠AOB的平分线,P是OC上任意一点,PD⊥OA,PE⊥OB,垂足分别是D,E(已知)，∴PD=PE(角平分线上的点到这个角的两边距离相等).逆定理在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上.OCB1A2PDE∵PA=PB,PD⊥OA,PE⊥OB,垂足分别是D,E(已知),∴点P在∠AOB的平分线上.(在一个角的内部,且到角的两边距离相等的点,在这个角的平分线上).用尺规作角的平分线.邻补角的角平分线之间的关系.小结与拓展 独立作业