七年级下数学课件《证明》课件2_苏科版

七年级下数学课件《证明》课件2_苏科版

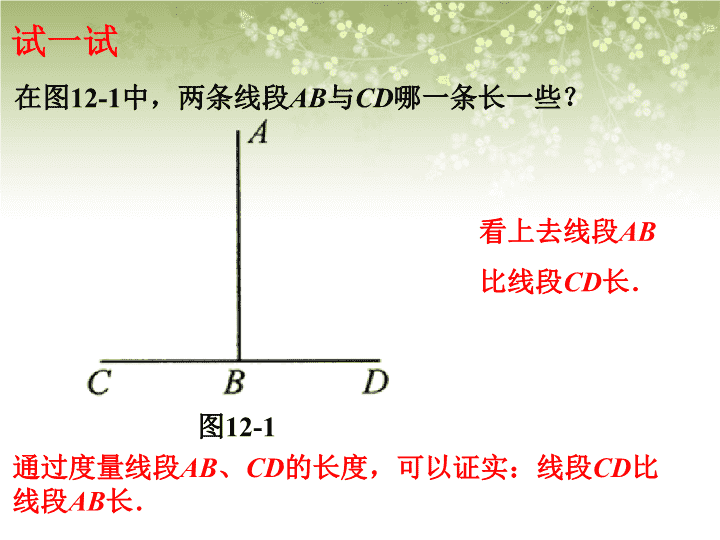
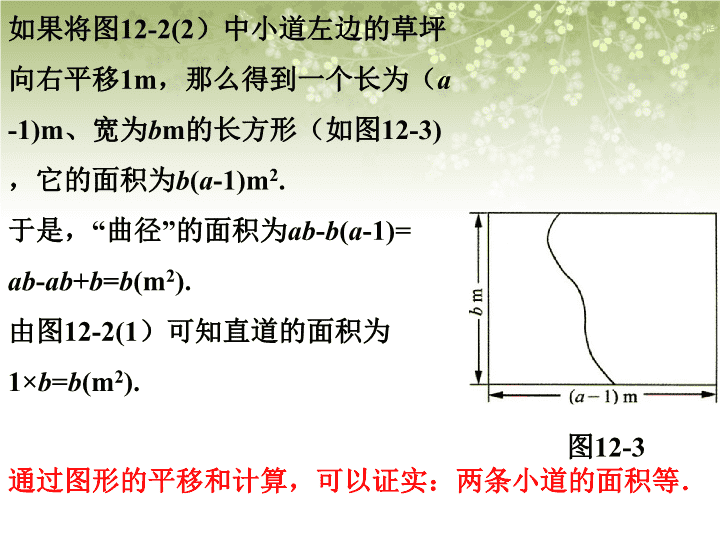
证明 在图12-1中，两条线段AB与CD哪一条长一些？图12-1看上去线段AB比线段CD长．通过度量线段AB、CD的长度，可以证实：线段CD比线段AB长．试一试 如果将图12-2(2）中小道左边的草坪向右平移1m，那么得到一个长为（a-1)m、宽为bm的长方形（如图12-3)，它的面积为b(a-1)m2.于是，“曲径”的面积为ab-b(a-1)=ab-ab+b=b(m2).由图12-2(1）可知直道的面积为1×b=b(m2).通过图形的平移和计算，可以证实：两条小道的面积等．图12-3 1．图12-4(l）是一张8×8的正方形纸片，把它剪成4块，按图12-4(2）重新拼合.这4块纸片恰好能拼成一个长为13、宽为5的长方形吗？图12-4 2．画∠AOB=90°，并画∠AOB的平分线OC.（1）把三角尺的直角顶点落在OC的任意一点P上，使三角尺的两条直角边分别与OA、OB相交于点E、F（如图12-5(1)）.度量PE、PF的长度，这两条线段相等吗？（2）把三角尺绕点P旋转（如图12-5(2)），PE与PF相等吗？在后续的学习中，可以证实：图12-4(2)不是长方形；图12-5中PE与PF相等．图12-5 命题，有真命题，也有假命题.要说明一个命题是假命题，只要举出反例即可.要说明一个命题是真命题，则要从命题的条件出发，根据已学过的基本事实、定义、性质、和定理等，进行有理有据的推理.这种推理的过程叫做证明(proof).经过证明的真命题称为定理（theorem). 例证明：平行于同一条直线的两条直线平行.已知：如图，直线a、b、c，a∥c，b∥c求证：a∥b.abc证明：如图，作直线d，分别与直线a、b、c相交.∵a∥c(已知）∴∠1=∠3(两直线平行，同位角相等)∵b∥c∴∠2=∠3(两直线平行，同位角相等.)∴∠1=∠3(等量代换)∴a∥b（同位角相等，两直线平行）即平行于同一条直线的两条直线平行.d123 第一步画出图形第二步写出已知、求证写出证明过程第三步根据题意根据条件、结论和图形分析、探索证明的步骤 已知:如图，直线AB和CD相交于点O.求证:∠1=∠2.1ABDC2(平角的定义)(平角的定义)(等量代换)(等式的性质)对顶角相等证明: 同角（或等角）的余角相等已知：求证：证明:（）（）（）（）（） 平行线的性质定理一　两条平行线被第三条直线所截，内错角相等．1.指出定理的条件和结论，并画出图形，结合图形写出已知、求证．2.说说你的证明思路，试着写出证明过程.一起探究 例1已知：如图12-7，直线AB、CD被直线EF所截，AB∥CD，MG平分∠EMB，NH平分∠END.求证：MG∥NH.证明：∵AB∥CD（已知），∴∠EMB=∠END（两直线平行，同位角相等）.∵MG平分∠EMB，NH平分∠END（已知），∴∠EMG=∠EMB，∠ENH=∠END（角平分线的定义）.∴∠EMG=∠ENH（等量代换）.∴MG∥NH（同位角相等，两直线平行）. 例.已知：如图，直线AB、CD与直线EF相交，且∠1=∠2.求证：AB∥CDFABDCE321证明：∵∠1=∠2(已知)又∵∠1=∠3(对顶角相等)∴∠2=∠3(等量代换)∴AB∥CD(同位角相等，两直线平行)一起探究 例2已知：如图12-9，AC、BD相交于点O.求证：∠A+∠B=∠C+∠D.证明：在△AOB中，∠A+∠B+∠AOB=180°（三角形三个内角的和等于180°）.∴∠A+∠B=180°-∠AOB（等式性质）.在△COD中，同理可得∠C+∠D=180°-∠COD.∵∠AOB=∠COD（对顶角相等）.∴∠A+∠B=∠C+∠D（等量代换）. 例.已知：如图，∠AOB=∠BOC=180°，OE平分∠AOB，OF平分∠BOC求证：OE⊥OF ∵OE平分∠AOB，OF平分∠BOC，(已知)∴∠1=∠AOB，∠2=∠BOC．(角平分线的定义)又∵∠AOB=∠BOC=180°，(已知)∴∠1+∠2=(∠AOB+∠BOC)=90°．(等式性质)∴OE⊥OF(垂直的定义) 补充完成下列各题的证明，并填上推理的依据.1.已知：如图，AB∥CD，AD∥BC.求证：∠A=∠C.证明：∵AB∥CD，()∴∠A＋∠D=180°.()∵AD∥BC，()∴∠C＋∠D=180°.()∴∠A＋∠D=∠C＋∠D()∴∠A=∠C.()已知条件两直线平行，同旁内角相等.已知条件两直线平行，同旁内角互补.角的性质与相同角互补的角相等 证明：∵DC∥AB，()∴∠ABD=∠CDB()∵DF平分∠CDB，BE平分∠ABD.()∴∠1=∠CDB，()∴∠2=∠ABD.()∴∠1=∠2.()2.已知：如图，DC∥AB，DF平分∠CDB，BE平分∠ABD.求证：∠1=∠2.两直线平行，内错角角相等.已知条件角平分线性质.已知条件角平分线性质.角的性质 三角形三个内角的和等于已知：△ABC.求证：∠A+∠B+∠C=180°180°命题的正确性还要严密的推理证明想一想：如何证明呢？三角形内角和定理： 21EDCBA则CE∥BA(同位角相等，两直线平行).∴∠1=∠A(两直线平行，内错角相等).∵B，C，D在同一直线上∴∠1+∠2+∠ACB=∠A+∠B+∠ACB=180°延长BC到D，在△ABC的外部，以CA为一边，CE为另一边作∠2=∠B， 在这里，为了证明的需要，在原来的图形上添画的线叫做辅助线.在平面几何里，辅助线通常画成虚线.为了证明三个角的和为1800，可以转化为一个平角，这种转化思想是数学中的常用方法. 问题如图，把△ABC的一边BC延长，得到∠ACD．这个角还是三角形的内角吗？概念：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．ABCD 问题如图，把△ABC的一边BC延长，得到∠ACD．这个角还是三角形的内角吗？概念：三角形的一边与另一边的延长线组成的角，叫做三角形的外角．ABCD ∠ACD（外角）+∠ACB（相邻的内角）=180°．ABCD问题如图，∠ACD与∠ACB的位置是怎样的？∠ACD与∠ACB有什么数量关系？ 如图，∵　∠ACD+∠ACB=180°，∠A+∠B+∠ACB=180°，∴∠ACD=∠A+∠B．ABCD问题如图，∠ACD与∠A，∠B的位置是怎样的？∠ACD与∠A，∠B的大小有什么关系？你能证明你的结论吗？ 三角形内角和定理的推论：三角形的一个外角等于与它不相邻的两个内角的和．三角形的外角大于与它不相邻的任何一个内角．推论是由定理直接推出的结论，和定理一样，推论可以作为进一步推理的依据． 1.根据题意，画出图形;2.分清命题的条件和结论，结合图形，在“已知”中写出条件，在“求证”中写出结论.3.在“证明”中写出推理过程.且每一步推理都要有依据证明几何命题的一般格式：课堂小结