七年级下数学课件《三角形的内角和外角》课件4第二课时_冀教版

七年级下数学课件《三角形的内角和外角》课件4第二课时_冀教版

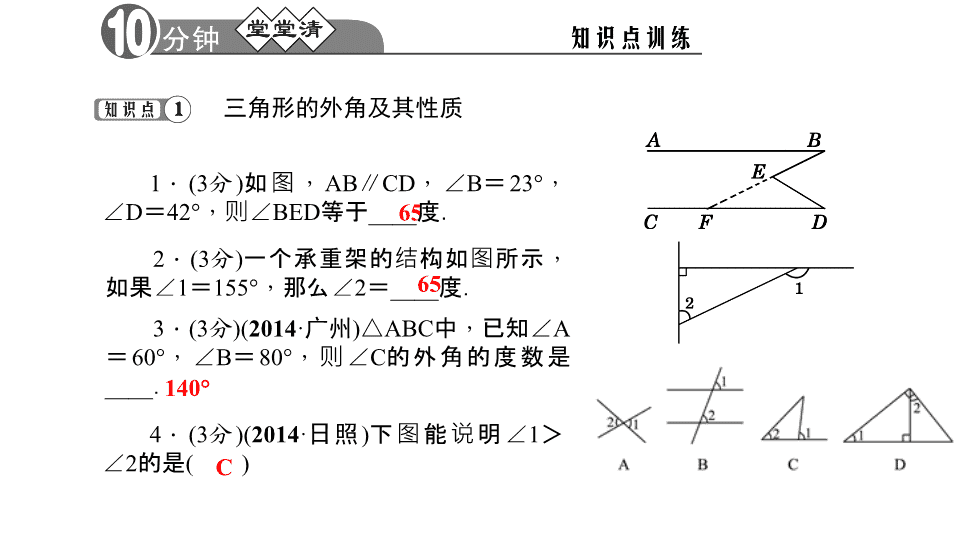
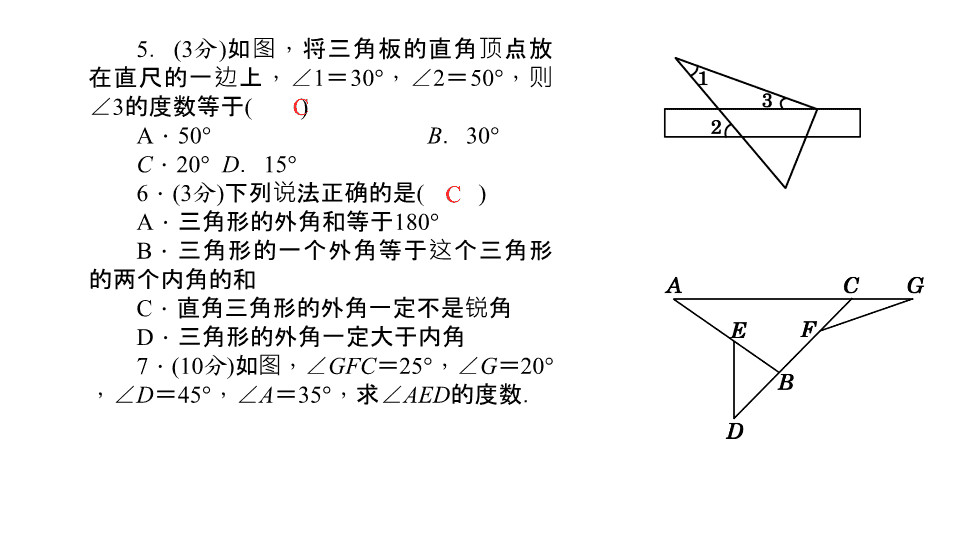
第2课时　三角形的外角得分________卷后分________评价________外角大于内角之和1．三角形的一边与另一边的延长线组成的角，叫做三角形的____．2．三角形的一个外角等于与它不相邻的两个___．3．三角形的一个外角____与它不相邻的任意一个内角．4．三个内角都是锐角的三角形叫做____，有一个内角是直角的三角形叫做____，有一个内角是钝角的三角形叫做____．锐角三角形直角三角形钝角三角形 6565140°三角形的外角及其性质2．(3分)一个承重架的结构如图所示，如果∠1＝155°，那么∠2＝____度．3．(3分)(2014·广州)△ABC中，已知∠A＝60°，∠B＝80°，则∠C的外角的度数是____．1．(3分)如图，AB∥CD，∠B＝23°，∠D＝42°，则∠BED等于____度．4．(3分)(2014·日照)下图能说明∠1＞∠2的是()C 5．(3分)如图，将三角板的直角顶点放在直尺的一边上，∠1＝30°，∠2＝50°，则∠3的度数等于()A．50°B．30°C．20°D．15°6．(3分)下列说法正确的是()A．三角形的外角和等于180°B．三角形的一个外角等于这个三角形的两个内角的和C．直角三角形的外角一定不是锐角D．三角形的外角一定大于内角7．(10分)如图，∠GFC＝25°，∠G＝20°，∠D＝45°，∠A＝35°，求∠AED的度数．CC 解：在△CGF中，∠G＝20°，∠GFC＝25°，∴∠ACB＝∠G＋∠GFC＝45°.在△ABC中，∠A＝35°，∠ACB＝45°，∴∠ABD＝∠A＋∠ACB＝80°.在△BDE中，∠ABD＝80°，∠D＝45°，∴∠AED＝∠D＋∠ABD＝125°三角形的分类8．(3分)已知△ABC的一个外角为50°，则△ABC一定是()A．锐角三角形B．直角三角形C．钝角三角形D．钝角或锐角三角形9．(3分)一个三角形三个内角的度数之比为2∶3∶4，这个三角形一定是()A．直角三角形B．锐角三角形C．等腰三角形D．钝角三角形10．(3分)如果等腰三角形两边长是6cm和3cm，那么它的周长是()A．9cmB．12cmC．15cm或12cmD．15cmCBD 11．(3分)下列叙述：①三角形三边互不相等；②三角形三边至少有两边相等；③三角形任意两边之和一定大于第三边；④三角形包括不等边三角形、等腰三角形和等边三角形；⑤三角形最多有两条边相等．正确的有____．(填序号)12．已知△ABC中，∠A，∠B，∠C的外角度数之比为2∶3∶4，则这个三角形是()A．直角三角形B．等边三角形C．钝角三角形D．等腰三角形13．如图，将三角尺的直角顶点放在直线a上，a∥b，∠1＝50°，∠2＝60°，则∠3的度数为()A．50°B．60°C．70°D．80°③CC 14．如图所示，下列结论正确的是()A．∠1＞∠2＞∠AB．∠1＞∠A＞∠2C．∠A＞∠2＞∠1D．∠2＞∠1＞∠A15．(2014·泰安)如图，把一直尺放置在一个三角形纸片上，则下列结论正确的是()二、填空题(每小题4分，共16分)16．一个三角形最多有____个直角，最多有____个钝角，最少有___个锐角．17．如图，∠A＝40°，∠B＝30°，∠D＝40°，则∠BED＝____度．D112110A 18．如图，∠BAC＝46°，∠B＝27°，∠C＝30°，则∠BDC＝____．19．根据下列图形填空：(1)如图①，在△ABC中，∠A＝45°，∠B＝60°，则外角∠ACD＝____度；(2)如图②，已知AC⊥BC，∠CBD＝148°，则∠A＝____；(3)如图③，x＝____．三、解答题(共28分)20．(8分)如图，AB∥CD，∠DAB＝37°，∠AEC＝85°，求∠BCD的度数．103°10558°60解：∠BCD＝48° 21．(10分)判断适合下列条件的△ABC是锐角三角形，直角三角形，还是钝角三角形．(1)∠A－∠B＝30°，∠B－∠C＝36°；(2)∠A∶∠B∶∠C＝1∶2∶3.解：(1)设∠B＝x°，则∠A＝(30＋x)°，∠C＝(x－36)°，所以x＋(30＋x)＋(x－36)＝180，解得x＝62，所以最大角∠A＝30°＋62°＝92°，所以△ABC是钝角三角形(2)设∠A＝x°，则∠B＝2x°，∠C＝3x°，所以x＋2x＋3x＝180，解得x＝30，所以最大角∠C＝3x°＝90°，所以△ABC是直角三角形 【综合运用】22．(10分)如图，D是AB上一点，E是AC上一点，BE，CD相交于点F，∠A＝62°，∠ACD＝35°，∠ABE＝20°，求：(1)∠BDC的度数；(2)∠BFC的度数．解：(1)在△ACD中，∵∠A＝62°，∠ACD＝35°，∴∠BDC＝∠A＋∠ACD＝62°＋35°＝97°(2)在△BDF中，∠BDC＝97°，∠ABE＝20°，∴∠BFC＝∠BDC＋∠ABE＝117°