七年级下数学课件《解二元一次方程组》 (6)_苏科版

七年级下数学课件《解二元一次方程组》 (6)_苏科版

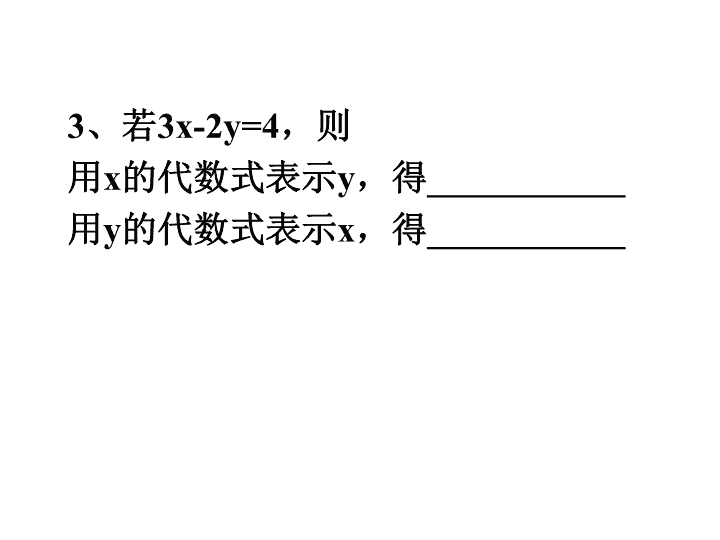
初中数学七年级下册 （苏科版） 1.二元一次方程组概念; 2.二元一次方程组的解. 3、若3x-2y=4，则 用x的代数式表示y，得___________ 用y的代数式表示x，得___________ 根据篮球比赛规则:赢一场得2分， 输一场得1分。在某次中学生篮 球联赛中，某球队赛了12场，赢 了x场，输了y场，积20分。请根 据题意列出方程组。 x+y=12 2x+y=20 如何解这个方程组呢？ x+y=12 2x+y=20 ① ②如何解 由① ，得y=12－x． ③ 由于方程组中相同的字母表示同一个未知数， 所以方程②中的y也等于12－x，可以用12－x代替 方程②中的y．这样就有2x+12－x=20．这个方程 不含y，是一元一次方程了． ①式中的y等于12－x 解方程组例1 x+y=12 2x+y=20 解： 把③代入②，得： 2x+12-x=20 解这个方程得：x=8 把x=8代入③得：y=4 所以原方程组的解是 x=8 y=4 代入，让“二元”化成 “一元” 解一元一次方 程，求出x的值。 再代入，求出y的值。 总结，写出 方程组的解。 ① ② 由①得，y=12-x ③ 变形，用含x的 代数表示y 一变，二代，三消，四解，五再代，六总结 你能通过消去x的方法解这个方程组 吗？ 解方程组      .1223 113 yx yx 将方程组的一个方程中的某个未知数 用含有另一个未知数的代数式表示，并 代入另一个方程，从而消去一个未知数， 把解二元一次方程组转化为解一元一次 方程，这种解方程组的方法称为代入消 元法，简称代入法． 代入消元法： 用代入法解二元一次方程组主要步骤： （1）用一个未知数表示另一个未知数； （2）代入消元； （3）解一元一次方程； （4）求方程组的解． 1．用代入法解方程组 ① ② 较为简便的方法是 ( ) A．先把①变形 B．先把②变形 C．可先把①变形，也可先把②变形 D．把①、②同时变形 2．用代入法解二元一次方程组 　　 ① ② 可直接把方程①代入方程②， 消去未知数 _______，得一元一次方程_______，解得y＝_______； 再把y＝_______代入方程①，解得x＝，所以方程组的解是_______． 用代入法解下列方程组： （1） （2）      154xy xy      5 3 yx yx （3）      132 42 yx yx （4）      089 07 yx yx 用代入法解下列方程组      .723 ,432 yx yx 用代入法解下列方程组： （1） （2）      1023 1263 yx yx      624 132 yx yx 1.用代入法解下列方程组： （1） （2）      1153 1173 xy yx      132 4 1 3 2 yx yx 先阅读材料，再解方程组． 解方程组 时，可由①得x－y＝1 ③， 然后再将③代入②，得4×1－y＝5，解得y＝－1， 从而可得 这种方法称为“整体代入”法． 请用上面的方法解方程组 (2)已知方程4x－y=10中，x与y互为相反数， 求x，y． （3）已知 是方程组 的解，求 的值．      1 2 y x      2 5 aybx byax a b 将方程组的一个方程中的某个未知数用含有另一个未知 数的代数式表示，并代入另一个方程，从而消去一个未 知数，把解二元一次方程组转化为解一元一次方程。这 种解方程组的方法称为代入消元法，简称为代入法。 1.代入消元法 2.代入法的基本思想：消元. 3.代入法解二元一次方程组主要步骤： （1）用一个未知数表示另一个未知数； （2）代入消元； （3）解一元一次方程； （4）求方程组的解．