初中数学7年级教案：第8讲 相交线与平行线综合

初中数学7年级教案：第8讲 相交线与平行线综合

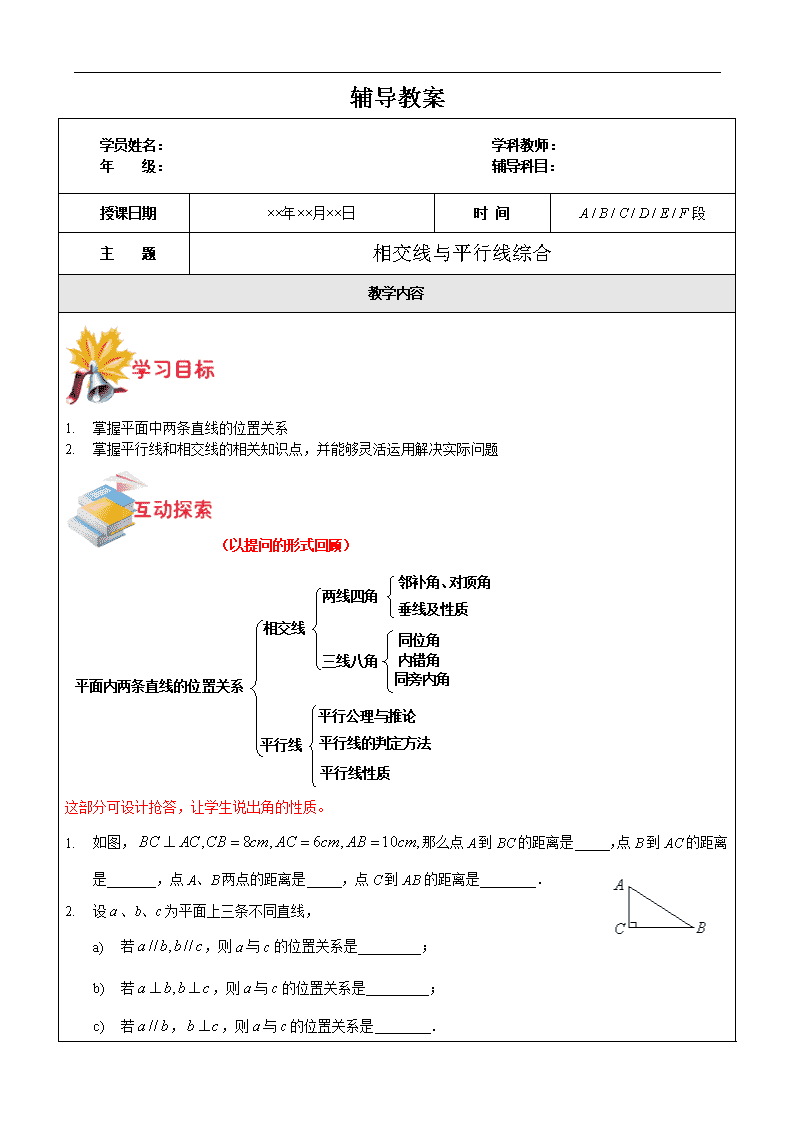
辅导教案 学员姓名： 学科教师：‎ 年 级： 辅导科目： ‎ 授课日期 ‎××年××月××日 ‎ 时 间 A / B / C / D / E / F段 主 题 相交线与平行线综合 教学内容 1. 掌握平面中两条直线的位置关系 2. 掌握平行线和相交线的相关知识点，并能够灵活运用解决实际问题 ‎（以提问的形式回顾）‎ 平面内两条直线的位置关系 相交线 平行线 平行线性质 平行线的判定方法 平行公理与推论 两线四角 邻补角、对顶角 垂线及性质 同位角 内错角 三线八角 同旁内角 这部分可设计抢答，让学生说出角的性质。‎ 1. 如图，那么点A到BC的距离是_____，点B到AC的距离是_______，点A、B两点的距离是_____，点C到AB的距离是________．‎ 2. 设、b、c为平面上三条不同直线，‎ a) 若，则a与c的位置关系是_________；‎ b) 若，则a与c的位置关系是_________；‎ c) 若，，则a与c的位置关系是________．‎ ‎1. 6cm 8cm 10cm 4.8cm.　2. 平行　平行　垂直　‎ ‎（采用教师引导，学生轮流回答的形式）‎ 例1. 下列说法正确的是（ ）‎ A、两条直线相交所构成的四个角中，如果有两个角相等，则这两条直线垂直 B、两条直线相交成直角，那么这两条直线垂直 C、垂直是两条直线在同一平面内的第三种位置关系 D、点到直线的距离是点到直线的垂线的长度 点拨：选项A中，两个角相等不能判断两直线垂直，∴A是错误的 选项C中，垂直是两直线相交的特殊情况∴C是错误的 选项D中，距离是垂线段的长度∴D是错误的 ‎∴选B 例2. 下列判断：①∠A与∠1是同位角；②∠A与∠B是同旁内角；③∠4与∠1是内错角；④∠1与∠3是同位角．其中正确的是（　 ）‎ 答案：①②③‎ 试一试：如图，图中∠1与∠2是同位角的是( ) ‎ ‎1‎ ‎2‎ ‎2‎ ‎1‎ ‎1‎ ‎2‎ ‎1‎ ‎2‎ ‎ ⑴ ⑵ ⑶ ⑷‎ ‎ （A）⑵ ⑶ （B）⑵ ⑶ ⑷ （C）⑴ ⑵ ⑷ （D）⑶ ⑷‎ 答案：B 例3. 已知：如图，D是BC上的一点．DE∥AC，DF∥AB．求证：∠A＋∠B＋∠C＝180°．‎ 证明：∵DE∥AC，‎ ‎∴∠=∠，∠+∠=180°‎ ‎∵DF∥AB ‎∴∠=∠，∠+∠=180°‎ ‎∴∠=∠‎ ‎∵∠+∠+∠=180°‎ ‎∴∠A＋∠B＋∠C＝180°‎ ‎（学生统一完成，互相批改，教师针对重难点详细讲解）‎ 一、选择题：‎ ‎1．下列说法中：①对顶角相等；②垂直于同一条直线的两直线平行；③相等的角是对顶角；④ 同位角相等。 ‎ 其中错误的有（ ）‎ A. 1个　　　 B. 2个　　 　C. 3个　　 　D. 4个 ‎2．如图，直线AB、CD相交于点O，OE⊥AB于O，∠DOE＝55°，则∠AOC的度数为（ ）‎ A. 40°　 　B. 45°　 C. 30°　　　 D. 35°‎ 3． 如图两条非平行的直线AB，CD被第三条直线EF所截，交点为PQ，那么这条直线将所在平面分成（ ）‎ A、5个部分 B、6个部分 C、7个部分 D、8个部分 ‎ （第2题） （第3题） （第4题）‎ ‎4．如图AB∥CD，AC⊥BC，图中与∠CAB互余的角有（ ）‎ A. 1个　　　 B. 2个　　 　C. 3个　　 　D. 4个 ‎5．图下列条件中，不能判断直线的是（ ）‎ A. ∠1=∠3 B. ∠2=∠3 ‎ C. ∠4=∠5 D. ∠2+∠4＝180°　‎ ‎6．如图已知∠1=∠2，∠BAD=∠BCD，则下列结论（1）AB∥CD， （2）AD∥BC， （3）∠B=∠D， ‎ ‎（4）∠D=∠ACB正确的有（ ）‎ A. 1个　　　 B. 2个　　 　C. 3个　　 　D. 4个 ‎（第5题） （第6题） （第8题）‎ 7． 如果两条直线被第三条直线所截，那么一组内错角的平分线（ ）‎ A. 互相垂直 B. 互相平行 C. 互相重合 D. 以上均不正确 8． 如图已知∠1+∠3=180°，则图中与∠1互补的角还有（ ）‎ A. 1个　　　 B. 2个　　 　C. 3个　　 　D. 4个 二、填空题 9． 如图点O是直线AB上的一点，OC⊥OD，∠AOC-∠BOD＝20°,则∠AOC＝ 。‎ ‎10．如图，直线a∥b，∠1=42°，则∠2＝ 0‎ ‎（第9题） （第10题） （第11题）‎ ‎11. 如图，直线a∥b，∠1＝70°，∠2＝35°，则∠3＝ , ∠4＝ 。‎ ‎12. 两个角的两边互相平行，其中一个角是另一个角的3倍，则这两个角的度数分别是 和 。‎ ‎ ‎ ‎13. 两条相交直线所形成的一个角为，则它们的夹角是__________.‎ ‎14. 如图，a∥b，点A1,、A2在直线a上，B、C在直线b上，则三角形A1BC面积与三角形__________‎ 的面积相等. ‎ ‎ ‎ 15. 如图，∠BAC=90°，AD⊥BC，垂足为D，则点A到BC的距离是线段__________的长度；线段CA的长度是__________点到直线__________的距离. ‎ ‎ ‎ ‎16. 如图，由a∥b可推得∠1=∠2，理由是 .‎ 由∠2=∠3可推得c∥d ，理由是 .‎ ‎（第14题） （第15题） （第16题）‎ 17. 由a∥b且b∥c，可推得a∥c，理由是________________________.‎ 18. 如图，在∠1、∠2、∠3、∠4、∠5、∠B、∠D、∠ACE中，与∠D是同位角的是 ；与∠2是内错角的是 .‎ ‎ ‎ 19. 如图，AEFC是折线，直线AB∥CD，试写出∠1、∠2、∠3、∠4的大小所满足的关系式____________________.‎ ‎ ‎ ‎（第18题） （第19题） ‎ ‎20.一辆汽车在公路上行驶，两次拐弯后仍在原来的方向上平行前进，如果第一次向右拐 ‎60°，则第二次向_____拐_______。‎ ‎21、如图，已知AB∥CD，证明：∠B +∠F +∠D =∠E +∠G ‎22、如图，已知∠ABE +∠DEB = 180°，∠1 =∠2，求证：∠F = ∠G 答案：1、B；2、D；3、C；4、C；5、B；6、C；7、D；8、C；9、145°；10、138°；11、105°，75°；12、45°，135°；13、30°；14、A2BC；15、AD，B，AC；16、两直线平行，同位角相等；同位角相等，两直线平行；17、平行的传递性；18、∠1、∠4、∠5、∠ACE；∠4、∠ACE；19、∠3>∠2>∠4>∠1；20、左，60°21、过E、G、F作平行线，22略 ‎ ‎ 本节课主要知识点：相交线与平行线的基本概念，平行线的判定与性质 ‎ ‎【巩固练习】‎ ‎1. 若一个角的两边与另一个角的两边互相平行，这个角的度数是30°，则另一个角的度数是＿＿＿＿＿‎ 答案：30°或150°‎ ‎2. 如图，△ABC中，D是BC中点，E是AD的中点，则_________；‎ 答案：‎ ‎3. 如图，AB∥ED，CM平分∠BCE，CN⊥CM，∠B＝60°，则∠DCN为= 答案：30°‎ ‎ ‎ ‎4. 如图，EF∥AD,∠1=∠2,∠BAC=70°，将求∠AGD的过程填写完整；‎ 解： 因为EF∥AD，‎ ‎ 所以∠2=____ (_________________________________)‎ ‎ 又因为∠1=∠2‎ ‎ 所以∠1=∠3 (__________________)‎ ‎ 所以AB∥_____ (___________________________________)‎ ‎ 所以∠BAC+______=180°(___________________________)‎ ‎ 因为∠BAC=70°‎ ‎ 所以∠AGD=_______°；‎ ‎【预习思考】‎ 复习实数和相交线平行线章节，下节课期中复习