新课标2020高考物理二轮复习专题五科学思维篇1活用“三大观点”解析力学综合问题讲义含解析

新课标2020高考物理二轮复习专题五科学思维篇1活用“三大观点”解析力学综合问题讲义含解析

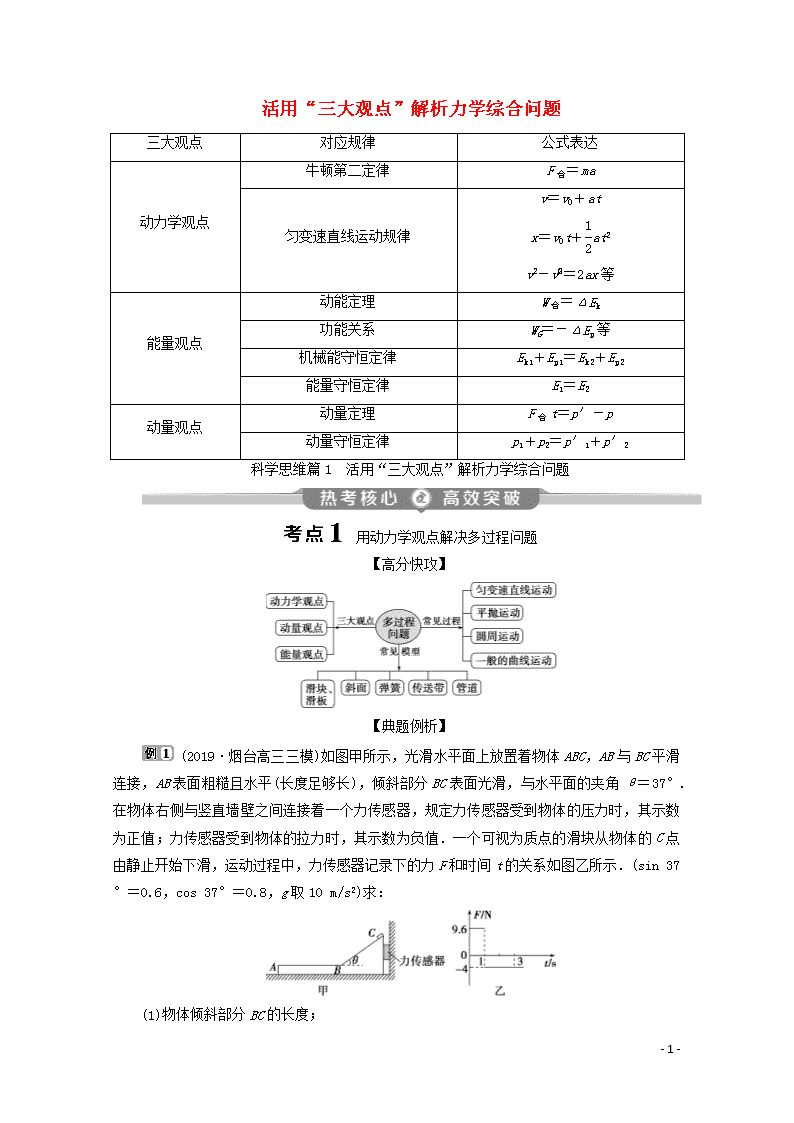
活用“三大观点”解析力学综合问题 三大观点 对应规律 公式表达 动力学观点 牛顿第二定律 F合＝ma 匀变速直线运动规律 v＝v0＋at x＝v0t＋at2‎ v2－v＝2ax等 能量观点 动能定理 W合＝ΔEk 功能关系 WG＝－ΔEp等 机械能守恒定律 Ek1＋Ep1＝Ek2＋Ep2‎ 能量守恒定律 E1＝E2‎ 动量观点 动量定理 F合t＝p′－p 动量守恒定律 p1＋p2＝p′1＋p′2‎ 科学思维篇1　活用“三大观点”解析力学综合问题 ‎　用动力学观点解决多过程问题 ‎【高分快攻】‎ ‎【典题例析】‎ ‎ (2019·烟台高三三模)如图甲所示，光滑水平面上放置着物体ABC，AB与BC平滑连接，AB表面粗糙且水平(长度足够长)，倾斜部分BC表面光滑，与水平面的夹角θ＝37°.在物体右侧与竖直墙壁之间连接着一个力传感器，规定力传感器受到物体的压力时，其示数为正值；力传感器受到物体的拉力时，其示数为负值．一个可视为质点的滑块从物体的C点由静止开始下滑，运动过程中，力传感器记录下的力F和时间t的关系如图乙所示．(sin 37°＝0.6，cos 37°＝0.8，g取10 m/s2)求：‎ ‎(1)物体倾斜部分BC的长度；‎ - 16 -‎ ‎(2)滑块的质量；‎ ‎(3)运动过程中滑块克服摩擦力做的功．‎ ‎[解析]　(1)对滑块在倾斜部分BC上的运动，由牛顿第二定律有mgsin θ＝ma1‎ 解得a1＝6 m/s2‎ 斜面BC长x1＝a1t＝3 m.‎ ‎(2)物体对传感器的压力为F1＝mgcos θsin θ，由题图乙可知F1＝9.6 N 解得m＝2 kg.‎ ‎(3)设1 s后物体ABC受到的摩擦力大小为f，对物体由平衡条件有f＝F2 ＝4 N 对滑块由牛顿第二定律有f＝ma2‎ 解得a2＝2 m/s2‎ 滑块在AB表面上滑行的距离x2＝ 而滑块到达B点处的速度v＝a1t1＝6 m/s2×1 s＝6 m/s 联立解得x2＝9 m 滑块克服摩擦力做的功为Wf＝fx2＝36 J.‎ ‎[答案]　(1)3 m　(2)2 kg　(3)36 J ‎【题组突破】‎ ‎1．(2017·高考全国卷Ⅱ)为提高冰球运动员的加速能力，教练员在冰面上与起跑线距离s0和s1(s1mgsin 37°＋μmgcos 37°＝0.8mg，故物体沿斜面向上运动，则物体在第4 s内的受力情况是受到平行斜面向下的摩擦力f′，竖直向下的重力G，垂直斜面向上的支持力N，平行斜面向上的力F(同学们可以自己画出受力分析图)．‎ 答案：(1)10 m/s2　(2)5 m/s2　(3)50 J　(4)见解析 ‎ ‎(1)动力学观点常用于求解恒力作用下的单体多过程直线运动或多体多过程直线运动．‎ ‎(2)牛顿运动定律是动力学的基础，也是高考命题的重点和热点．牛顿运动定律与匀变速直线运动规律相结合，常用于解决斜面问题、滑块木板问题、传送带问题等．‎ ‎(3)物体的受力情况往往与运动情况相联系，因此，应结合实际情况，将物体运动过程分为多个阶段，再分析每个阶段物体的运动规律和受力情况，同时注意各阶段间的速度关系和位移关系．　 ‎ ‎　用能量观点解决力学综合问题 ‎【高分快攻】‎ ‎1．若过程只有动能和势能的相互转化，应首先考虑应用机械能守恒定律．‎ ‎2．若过程涉及摩擦力做功，一般应考虑应用动能定理或能量守恒定律．‎ ‎3．若过程涉及电势能和机械能之间的转化，应考虑应用能量守恒定律．‎ ‎4．复杂问题的分析一般需选择能量的观点、运动与力的观点综合解题．‎ ‎【典题例析】‎ ‎ 轻质弹簧原长为2l，将弹簧竖直放置在地面上，在其顶端将一质量为5m的物体由静止释放，当弹簧被压缩到最短时，弹簧长度为l.现将该弹簧水平放置，一端固定在A点，另一端与物块P接触但不连接．AB是长度为5l的水平轨道，B端与半径为l的光滑半圆轨道BCD相切，半圆的直径BD竖直，如图所示．物块P与AB间的动摩擦因数μ＝0.5.用外力推动物块P，将弹簧压缩至长度l，然后放开，P开始沿轨道运动．重力加速度大小为g.‎ ‎(1)若P的质量为m，求P到达B点时速度的大小，以及它离开圆轨道后落回到AB上的位置与B点之间的距离；‎ ‎(2)若P能滑上圆轨道，且仍能沿圆轨道滑下，求P的质量的取值范围．‎ ‎[解析]　(1)依题意，当弹簧竖直放置，长度被压缩至l时，质量为5m的物体的动能为零，其重力势能转化为弹簧的弹性势能．由机械能守恒定律，弹簧长度为l时的弹性势能 Ep＝5mgl ①‎ 设P的质量为M，到达B点时的速度大小为vB，由能量守恒定律得Ep＝Mv＋μMg·4l②‎ - 16 -‎ 联立①②式，取M＝m并代入题给数据得vB＝ ③‎ 若P能沿圆轨道运动到D点，其到达D点时的向心力不能小于重力，即P此时的速度大小v应满足 －mg≥0 ④‎ 设P滑到D点时的速度为vD，由机械能守恒定律得 mv＝mv＋mg·2l ⑤‎ 联立③⑤式得vD＝ ⑥‎ vD满足④式要求，故P能运动到D点，并从D点以速度vD水平射出．设P落回到轨道AB所需的时间为t，由运动学公式得2l＝gt2 ⑦‎ P落回到轨道AB上的位置与B点之间的距离为 s＝vDt ⑧‎ 联立⑥⑦⑧式得s＝2l. ⑨‎ ‎(2)为使P能滑上圆轨道，它到达B点时的速度不能小于零．由①②式可知5mgl>μMg·4l⑩‎ 要使P仍能沿圆轨道滑回，P在圆轨道上的上升高度不能超过半圆轨道的中点C.由机械能守恒定律有 Mv≤Mgl ⑪‎ 联立①②⑩⑪式得m≤M

查看更多