高一数学必修3课件-2用样本的数字特征 估计总体的数字特征

高一数学必修3课件-2用样本的数字特征 估计总体的数字特征

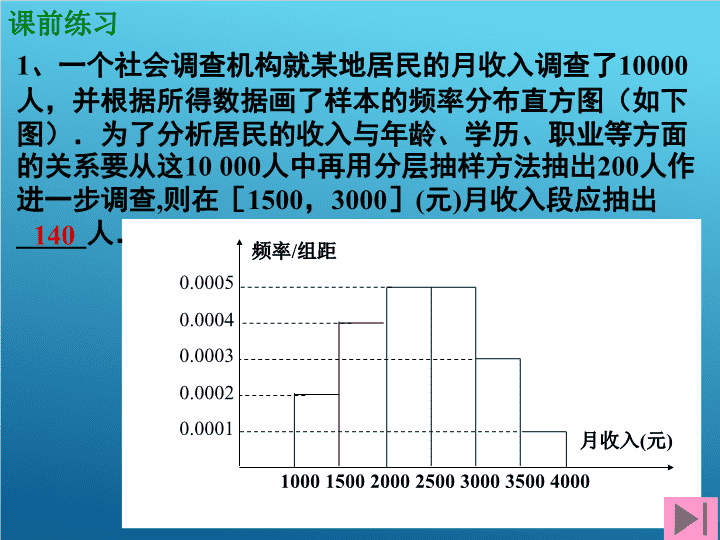
0.0001 0.0002 0.0003 0.0004 0.0005 1000 1500 2000 2500 3000 3500 4000 月收入(元) 频率/组距 1、一个社会调查机构就某地居民的月收入调查了10000 人，并根据所得数据画了样本的频率分布直方图（如下 图）．为了分析居民的收入与年龄、学历、职业等方面 的关系要从这10 000人中再用分层抽样方法抽出200人作 进一步调查,则在［1500，3000］(元)月收入段应抽出 _____人．140 课前练习 2、一个容量为40的样本数据分组后组数与频数如下： ［25，25.3）,6;［25.3，25.6）,4;［25.6，25.9）,10; ［25.9，26.2）,8;［26.2，26.5）,8;［26.5，26.8）,4； 则样本在［25，25.9）上的频率为（　　） 3 1 1 1 20 10 2 4A B C D、 　　 、 　　 、 　　 、 C 课前练习 ⑵中位数：将一组数据按大小依次排列，把处在最中 间位置的一个数据（或最中间两个数据的平均数）叫 做这组数据的中位数． ⑴众数：在一组数据中，出现次数最多的数据叫做这 组数据的众数． 众数、中位数、平均数都是描述一组数据的集中 趋势的特征数，只是描述的角度不同，其中以平均数 的应用最为广泛. ⑶平均数：一组数据的算术平均数，即 1 2 1 ( )nx x x xn      一、基础知识讲解 （一）基本概念 （二）众数、中位数、平均数与频率分布直方图的关系 1、众数在样本数据的频率分布直方图中，就是最 高矩形的中点的横坐标。 频率 组距 0.1 0.2 0.3 0.4 0.5 O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 例如，在上一节调查的100位居民的 月均用水量的问题中，从这些样本数 据的频率分布直方图可以看出，月均 用水量的众数是2.25t. 如图所示： 2、在样本中，有50％的个体小于或等于中位数，也有 50％的个体大于或等于中位数，因此，在频率分布直方 图中，中位数左边和右边的直方图的面积应该相等，由 此可以估计中位数的值。 频率 组距 0.1 0.2 0.3 0.4 0.5 O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) 下图中虚线代表居民月均用水量的中位 数的估计值，此数据值为2.02t. 说明: 2.02这个中位数的估计值，与样本的 中位数值2.0不一样，这是因为样本数据的 频率分布直方图，只是直观地表明分布的 形状，但是从直方图本身得不出原始的数 据内容，所以由频率分布直方图得到的中 位数估计值往往与样本的实际中位数值不 一致。 3、可以从频率分布直方图中估计平均数。平均数是 频率分布直方图的“重心”等于频率分布直方图中每 个小矩形的面积乘以小矩形底边中点的横坐标之和。 频率 组距 0.1 0.2 0.3 0.4 0.5 O 0.5 1 1.5 2 2.5 3 3.5 4 4.5 月平均用水量(t) (三)三种数字特征的优缺点 ⑴众数体现了样本数据的最大集中点，但它对其它数 据信息的忽视使得无法客观地反映总体特征。如上例 中众数是2.25t，它告诉我们，月均用水量为2.25t的居 民数比月均用水量为其它数值的居民数多，但它并没 有告诉我们多多少。 ⑵中位数是样本数据所占频率的等分线，它不受少数 几个极端值的影响，这在某些情况下是优点，但它对 极端值的不敏感有时也会成为缺点。如上例中假设有 某一用户月均用水量为10t，那么它所占频率为0.01,几 乎不影响中位数,但显然这一极端值是不能忽视的。 ⑶由于平均数与每一个样本的数据有关，所以任何一 个样本数据的改变都会引起平均数的改变，这是众数、 中位数都不具有的性质。也正因如此 ，与众数、中位 数比较起来，平均数可以反映出更多的关于样本数据 全体的信息，但平均数受数据中的极端值的影响较大， 使平均数在估计时可靠性降低。 例1、某工厂人员及工资构成如下： 人员 经理 管理人员 高级技工 工人 学徒 合计 周工资 2200 250 220 200 100 人数 1 6 5 10 1 23 合计 2200 1500 1100 2000 100 6900 （1）指出这个问题中周工资的众数、中位数、平均数。 （2）这个问题中，工资的平均数能客观地反映该厂的 工资水平吗？为什么？ 二、应用举例 分析：众数为200，中位数为220，平均数为300。 因平均数为300，由表格中所列出的数据可见，只有 经理在平均数以上，其余的人都在平均数以下，故用 平均数不能客观真实地反映该工厂的工资水平。 有两位射击运动员在一次射击测试中各射靶10次，每次命 中的环数如下： 甲：7 8 7 9 5 4 9 10 7 4 乙：9 5 7 8 7 6 8 6 7 7 问题：如果你是教练，你应当如何对这次射击作出评价? 如果看两人本次射击的平均成绩，由于 7 7x x    甲 乙， 两人射击的平均成绩是一样的。那么两个人的水 平就没有什么差异吗? 平均数向我们提供了样本数据的重要信息，但是平均数有时 也会使我们作出对总体的片面判断。因为这个平均数掩盖了一些 极端的情况，而这些极端情况显然是不能忽略的。因此，只有平 均数还难以概括样本数据的实际状态。 （四）标准差 4 5 6 7 8 9 10 环数 频率 0.1 0.2 0.3 (甲) 4 5 6 7 8 9 10 0.1 0.2 0.3 0.4 环数 频率 (乙) 直观上看，还是有差异的。如：甲成绩比较分散，乙成 绩相对集中(如图示)。 即甲、乙的成绩相对于他们的平均成绩的离散程度不同。 在数学中，刻画数据相对于平均数的离散程度，经常 用标准差或方差 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn          1 2, ,... ,nx x x x假设样本数据是 表示这组数据的平均数,则 表示这组数据的标准差 2s  标准差的平方 方差 2 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn             直观上看，还是有差异的。如：甲成绩比较分散，乙成 绩相对集中(如图示)。因此，我们还需要从另外的角度 来考察这两组。例如：在作统计图、表时提到过的极差。 甲的环数极差=10-4=6 乙的环数极差=9-5=4. 考察样本数据的分散程度的大小,最常用的统计量是标准 差.标准差是样本平均数的一种平均距离,一般用s表示． 所谓“平均距离”，其含义可作如下理解： 1 2, ,... , ,n ix x x x x x  假设样本数据是 表示这组数据的平均数 到 的距离是 ( 1,2, , )ix x i n   1 2 nx x x x x x S n        由于上式含有绝对值，运算不太方便，因此，通 常改用如下公式来计算标准差 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn          1 2, ,... , ,n ix x x x x x  假设样本数据是 表示这组数据的平均数 到 的距离是 （四）标准差 由 可以知道,甲的成绩离散程度大,乙的成绩 离散程度小.由此可以估计,乙比甲的射击成绩稳定. 1 2 2 x x 显然，标准差越大，则a越大，数据的离散程度越 大；标准差越小，数据的离散程度越小。 用计算器可得 s s甲 乙 2 1 095s s  甲 乙， 上面两组数据的离散程度与标准差之间的关系可 用图直观地表示出来. 4 5 6 7 8 9 10 s甲 s乙 1x 2x a 1 2 2 1 2 1 , .2 2 x x x x x xa    其样本的标准差为 ，记 一个样本中的个体与平均数之间的距离关系可用下图表示: 考虑一个容量为2的样本: 例2、画出下列四组样本数据的条形图,说明它们的异同点. (1) 5，5，5，5，5，5，5，5，5； (2) 4，4，4，5，5，5，6，6，6； (3) 3，3，4，4，5，6，6，7，7； (4) 2，2，2，2，5，8，8，8，8； 解：四组样本数据的条形图是: 二、应用举例 5x   S=0.00 频率 o 1 2 3 4 5 6 7 8 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 (1) 5x   S=0.82 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 (2) 频率 o 1 2 3 4 5 6 7 8 5x   S=1.49 5x   S=2.83 四组数据的平均数都是5.0，标准差分别是0.00， 0.82，1.49，2.83。 虽然它们有相同的平均数，但是它们有不同的标 准差，说明数据的分散程度是不一样的。 1 2 3 4 5 6 7 8 频率 o 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 (3) 频率 o 1 2 3 4 5 6 7 8 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 (4) 标准差还可以用于对样本数据的另外一种解释。例 如，在关于居民月均用水量的例子中，平均数： 1.973x  标准差s=0.868 ，所以 2.841, 2 3.709 1.105, 2 0.237. x s x s x s x s             100 ,这 个数据中  [ 2 , 2 ] 0.237,3.709 4x s x s     在区间 外的只有 个 2 , 2 ]x s x s    也就是说[ 几乎包含了所有样本数据 2, : s  标准差的平方 方从数学的角度考虑 人们有时用 来代替标准差，作为测量样本数据分散程度的工具 差 2 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn             例2、甲乙两人同时生产内径为25.40mm的一种零件.为 了对两人的生产质量进行评比,从他们生产的零件中各抽 出20件,量得其内径尺寸如下(单位:mm) 甲 25.46, 25.32, 25.45, 25.39, 25.36 25.34, 25.42, 25.45, 25.38, 25.42 25.39, 25.43, 25.39, 25.40, 25.44 25.40, 25.42, 25.35, 25.41, 25.39 乙 25.40, 25.43, 25.44, 25.48, 25.48 25.47, 25.49, 25.49, 25.36, 25.34 25.33, 25.43, 25.43, 25.32, 25.47 25.31, 25.32, 25.32, 25.32, 25.48 从生产的零件内径的尺寸看,谁生产的质量较高? 解:用计算器计算可得: 25.401 25,406; 0.037 0.068 x x s s     甲 乙 甲 乙 ， ， . s s甲 乙，因此甲生产的零件内径比乙的稳定 程度高得多，于是可以作出判断，甲生产的零件 的质量比乙的高一些 从样本平均数看,甲生产的零件内径比乙生产的更 接近内径标准(25.40mm),但是差异很小;从样本标准 差看,由于： 例3、求下列数据的标准差和方差 （1）5，7，7，8，10，11 （2）10，14，14，16，20，22 （3）7，9，9，10，12，13   1 2 1 2 1 , ,...... , ,...... ( ) 2 n m x x x h y y y k h k nh mk mh nk h kA B C Dm n m n m n        、已知两组样本数据 的平均数为 ， 的平均数为 ，则把两组数据合并成 一组以后，这组样本的平均数为 、 、 、 、 B 四、针对性练习 2、已知一组数据为-1, 0, 4, x , 6, 15, 且这组数据的中位 数为5, 那么这组数据的众数为( ) A、4 B、5 C、6 D、15 C 3、如果一组数中每个数加上同一个非零常数，则这 一组数的( )． A、平均数不变，标准差不变 B、平均数改变，标准差改变 C、平均数不变，标准差改变 D、平均数改变，标准差不变 D 四、针对性练习 2 ( ) 1 2 42 s A s B s C s D s 4、一组数据的标准差是 ，将这组数据中的每个数据 都乘以 ，得到的一组新数据的标准差是 、 、 、 、 C 1 2 8 1 2 8 5 , , , 6 2 2 6,2 6, ,2 6 x x x x x x     、数据 的平均数为 ，标准差为 ，则数据 的平均数为 ，方差为 166 四、针对性练习 9 10 11 50, 20x y x y      即 2 21 1 ( 10) ( 10) 10x y      2 2 2 20( ) 192, ( ) 2 20( ) 192, 96 x y x y x y xy x y xy           96 6 9 10 11 10 2 ___ . x y xy  、已知样本 ， ， ， ， 的平均数是 ， 标准差是 ，则 27 40 56 2 _____, ______ . 、若 个数据的平方和是 ，平均数是 ，则 这组数据的方差是 标准差是 9 10 3 10 10 四、针对性练习 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn          2 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn             2.标准差计算公式 3.方差计算公式 1.学会从频率分布直方图中估计众数、中位数、平均数 五、课时小结