天津高三数学理科试题精选分类汇编13:导数
最新2013届天津高三数学理科试题精选分类汇编13:导数
一、选择题
.(天津市蓟县二中2013届高三第六次月考数学(理)试题)函数 的图象与x轴所围成的封闭图形的面积为( )
( )
A. B.1 C.2 D.
.(天津市耀华中学2013届高三第一次月考理科数学试题)已知函数,则的大小关系是 ( )
A. B.
C. D.
.(天津市天津一中2013届高三上学期一月考理科数学).定义在R上的可导函数f(x),且f(x)图像连续,当x≠0时, ,则函数的零点的个数为 ( )
A.1 B.2 C.0 D.0或2
.(天津市新华中学2012届高三上学期第二次月考理科数学)已知函数满足,且的导函数,则的解集为 ( )
A. B. C. D.
二、填空题
.(天津市六校2013届高三第二次联考数学理试题(WORD版))若f(x)在R上可导,f(x)=x2+2f’(2)+3,则 .
.(天津南开中学2013届高三第四次月考数学理试卷)若不等式对任意都成立,则实数a取值范围是________.
.(天津市耀华中学2013届高三第一次月考理科数学试题)计算= ;
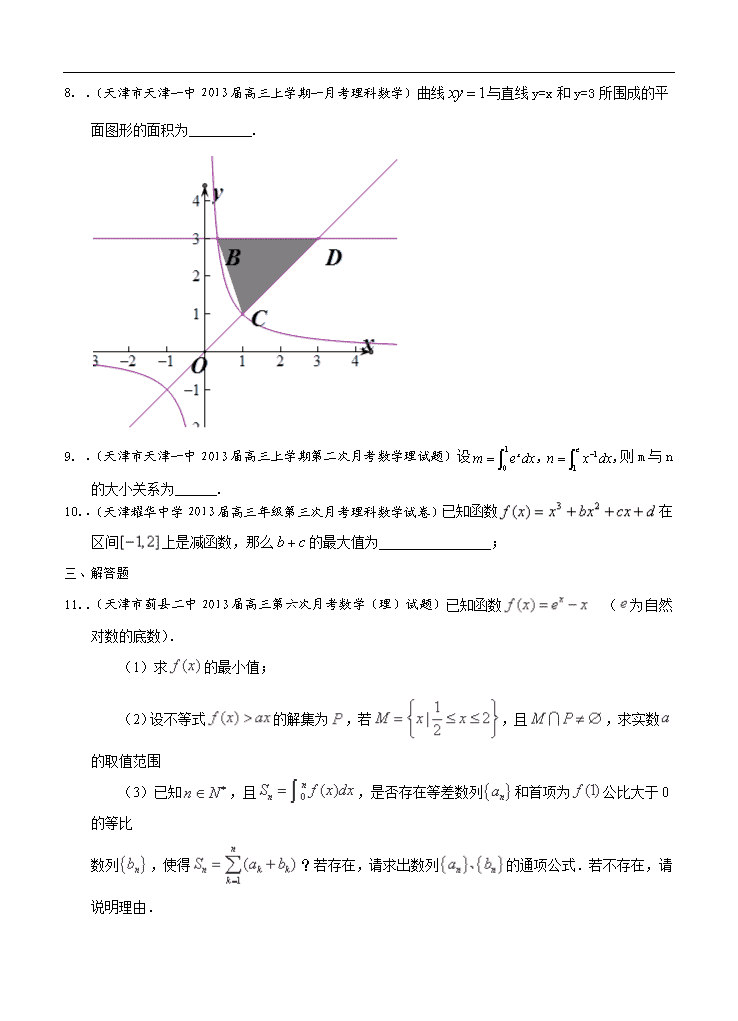
.(天津市天津一中2013届高三上学期一月考理科数学)曲线与直线y=x和y=3所围成的平面图形的面积为_________.
.(天津市天津一中2013届高三上学期第二次月考数学理试题)设,,则m与n的大小关系为______.
.(天津耀华中学2013届高三年级第三次月考理科数学试卷)已知函数在区间上是减函数,那么的最大值为________________;
三、解答题
.(天津市蓟县二中2013届高三第六次月考数学(理)试题)已知函数 (为自然对数的底数).
(1)求的最小值;
(2)设不等式的解集为,若,且,求实数的取值范围
(3)已知,且,是否存在等差数列和首项为公比大于0的等比
数列,使得?若存在,请求出数列的通项公式.若不存在,请说明理由.
.(天津市蓟县二中2013届高三第六次月考数学(理)试题) 已知函数().
(1)若,试确定函数的单调区间;
(2)若函数在其图象上任意一点处切线的斜率都小于,求实数的取值范围.
(3)若,求的取值范围.
.(天津市十二区县重点中学2013届高三毕业班联考(一)数学(理)试题)已知函数
(Ⅰ)若为的极值点,求实数的值;
(Ⅱ)若在上为增函数,求实数的取值范围;
(Ⅲ)当时,方程有实根,求实数的最大值.
2013年天津市十二区县重点学校高三毕业班联考(一
.(天津市六校2013届高三第二次联考数学理试题(WORD版))已知函数f(x)=2lnx+ax2-1(a∈R)
(1)求函数f(x)的单调区间;
(2)若a=1,分别解答下面两题,
(i)若不等式f(1+x)+f(1-x)
2.
.(天津南开中学2013届高三第四次月考数学理试卷)已知函数的最小值为0,其中.
(1)求a的值
(2)若对任意的,有成立,求实数k的最小值
(3)证明
.(2012-2013-2天津一中高三年级数学第四次月考检测试卷(理))已知函数在处取得极值.
(1)求实数的值;
(2)若关于的方程在区间上恰有两个不同的实数根,求实数的取值范围;
(3)证明:对任意的正整数,不等式都成立.
.(天津市耀华中学2013届高三第一次月考理科数学试题)(本小题满分14分)设函数,其中b≠0。
(1)当b>时,判断函数在定义域上的单调性;
(2)求函数的极值点;
(3)证明对任意的正整数n,不等式都成立。
.(天津市耀华中学2013届高三第一次月考理科数学试题)(本小题满分14分)设函数
(1)当a=1时,求曲线在点处的切线方程;
(2)若函数在其定义域内为增函数,求实数a的取值范围;
(3)设函数,若在[l,e]上至少存在一点使成立,求实数a的取值范围。
.(天津市天津一中2013届高三上学期一月考理科数学)已知函数f(x)=aln(ex+1)-(a+1)x,g(x)=x2-(a-1)x-f(lnx), a∈R,且g(x)在x=1处取得极值.
(1)求a的值;
(2)若对0≤x≤3, 不等式g(x)≤|m-1|成立,求m的取值范围;
(3)已知∆ABC的三个顶点A,B,C都在函数f(x)的图像上,且横坐标依次成等差数列,讨
论∆ABC是否为钝角三角形,是否为等腰三角形.并证明你的结论.
.(天津市天津一中2013届高三上学期一月考理科数学)已知函数f(x)=(x2+ax-2a2+3a)ex(x∈R),其中A∈R.
(1)当a=0时,求曲线y=f(x)在点(1,f(1))处的切线的斜率;
(2)当a≠2/3时,求函数f(x)的单调区间与极值.
.(天津市新华中学2012届高三上学期第二次月考理科数学)已知函数f(x)=ax-(2a+1)x+2lnx(a∈R).
(1)若曲线y=f(x)在x=1和x=3处的切线互相平行,求a的值;
(2)求f(x)的单调区间;
(3)设g(x)=x-2x,若对任意x∈(0,2],均存在x∈(0,2],使得f(x)0.(1)求f(x)的单调区间;(2)当x>0时,证明不等式:0, 递增区间是,递减区间是
(Ⅱ)(ⅰ)
设,
化简得:, ,
,在上恒成立,在上单调递减,
所以,,即的取值范围是
(ⅱ),在上单调递增,
①若,则则与已知
矛盾,
②若,则则与已知矛盾,
③若,则,又,得与矛盾,
④不妨设,则由(Ⅱ)知当时,,
令,则,
又在上单调递增,即
证2;
,
设,则t>0,,,
令,得,在(0,1)单调递减,在单调递增,
,又因为时,,不成立.
,
解:(1)的定义域为
,由,得,
当x变化时,的变化情况如下表:
x
-
0
+
↘
极小值
↗
因此,在处取得最小值,故由题意,所以.
(Ⅱ)解:当时,取,有,故不合题意.
当时,令,即.
,令,得
-1.
(1)当时,在上恒成立,因此在上单调递减,从而对于任意的,总有,即在上恒成立.
故符合题意.
(2)当时,,对于,,故在内单调递增,因此当取时,,即不成立.
故不合题意,
综上,k的最小值为.
(Ⅲ)证明:当n=1时,不等式左边=右边,所以不等式成立.
当时,
.
在(Ⅱ)中取,得,从而
,
所以有
.
综上,.
解:(1) …………1分
时,取得极值, …………2分
故解得经检验符合题意. …………3分
(2)由知 由,得
令则在区间上恰有两个不同的实数根等价于在区间上恰有两个不同的实数根.
当时,,于是在上单调递增;
当时,,于是在上单调递减.…………6分
依题意有,
解得, …………9分
(3) 的定义域为,由(1)知,
令得,或(舍去), 当时, ,单调递增;
当时, ,单调递减. 为在上的最大值. …11分
,故(当且仅当时,等号成立)
对任意正整数,取得, …………12分
故. …………14分
(方法二)数学归纳法证明:
当时,左边,右边,显然,不等式成立.
假设时,成立,
则时,有.做差比较:
构建函数,则,
单调递减,.
取,
即,亦即,
故时,有,不等式成立.
综上可知,对任意的正整数,不等式都成立.
解:(1),,
依题设,有,所以a=8.
(2)
,由,得或
函数增区间(0,1),减区间(1,3)
函数在x=3处取得极小值,g(x)min=g(3);函数g(x)在x=1处取得极大值g(x)max=g(1),
不等式|m-1|≥g(x),对0≤x≤3成立,等价于|m-1|≥g(x)max成立
即m-1≥g(x)max=g(1)orm-1≤-g(x)max=-g(1), m≤1-g(1) or m≥1+g(1)
(3)设,.,且,,
则,
∴,,
∴.
所以B为钝角,ABC是钝角三角形.
,
=
=
∵∴
∴ ∴
∴,故f(x)是R上的凹函数.
恒成立∴在上单调递减.
若ABC是等腰三角形,则只能是.
即
∵∴.
∴,
这与f(x)是R上的凹函数矛盾,故ABC是钝角三角形,但不可能是等腰三角形.
(1)解:
(2)
以下分两种情况讨论。
(1)>,则<.当变化时,的变化情况如下表:
+
0
—
0
+
↗
极大值
↘
极小值
↗
(2)<,则>,当变化时,的变化情况如下表:
+
0
—
0
+
↗
极大值
↘
极小值
↗
(1)f′(x)=ax-(2a+1)+ f′(1)=f′(3)
∴a-2a-1+2=3a-2a-1+
∴-a+1=a- a=
(2)注x>0!
f′(x)=
∵x>0 ∴令f′(x)>0得ax-(2a+1)x+2>0
<1>a=0时,得x<2 ∴f(x)在(0,2)在(2,+)
a0时,f′(x)>0得(x-2)(ax-1)>0
<2>a<0时,f′(x)>0得(x-2)(x-)<0
∴f(x)在(0,2)在(2,+)
<3>a>0时f′(x)>0得(x-2)(x-)>0
①=2 即a=时,f(x)在(0,+)
②>2 即0时,f(x)在(0,)在(2, +)在(,2)
(3)f(x)ln2-1
∴ln2-1时,f(x)在(0,)在(,2)
∴f(x)=f()=·-(2a+1)·+2ln
=-2--2lna
=2-2lna-
=-2(1+lna)-
∵a> ∴lna>ln>ln=-1 ∴f()<0 ∴a>
经上 a>ln2-1
【解】(Ⅰ),,
①,函数在上单调递增
②,,函数的单调递增区间为
,函数的单调递减区间为
(Ⅱ)存在,使得成立
等价于:,
考察, ,
递减
极(最)小值
递增
由上表可知:,
,
所以满足条件的最大整数;
(Ⅲ)当时,恒成立
等价于恒成立,
记,所以
, .
记,,
即函数在区间上递增,
记,,
即函数在区间上递减,
取到极大值也是最大值
所以
另解,,
由于,,
所以在上递减,
当时,,时,,
即函数在区间上递增,
在区间上递减,
所以,所以
解:(1)f’(x)=(x>-1,a>0)
令f’(x)=0
f(x)在(-1,)为减,在(,+)为增 f(x)min=f()=1-(a+1)ln(+1)
(2)设F(x)=ln(x+1)-
F’(x)=F(x)在(0,+)为增函数
F(x)>F(0)=0 F(x)>0即
G(x)=x-ln(x+1)(x>0)
G’(x)=1- G(x)在(0,+)为增函数
G(x)>G(0)=0 G(x)>0即ln(x+1)0,
则当,即时,在x>0上恒成立,故当时,在上单调递增;
③若p<0,的图像的对称轴为,,则在x>0上恒成立,故当p<0时,在上单调递减.
综上所述,
(3)令,则原问题等价于是否存在x0>0使得成立,故只需满足即可.
因为
而,故,
故当时,,则在上单调递减;当时,,则在上单调递增.
易知与上述要求的相矛盾,故不存在使得成立.