【数学】2020届一轮复习（理）通用版7-2二元一次不等式(组)与简单的线性规划问题学案

【数学】2020届一轮复习（理）通用版7-2二元一次不等式(组)与简单的线性规划问题学案

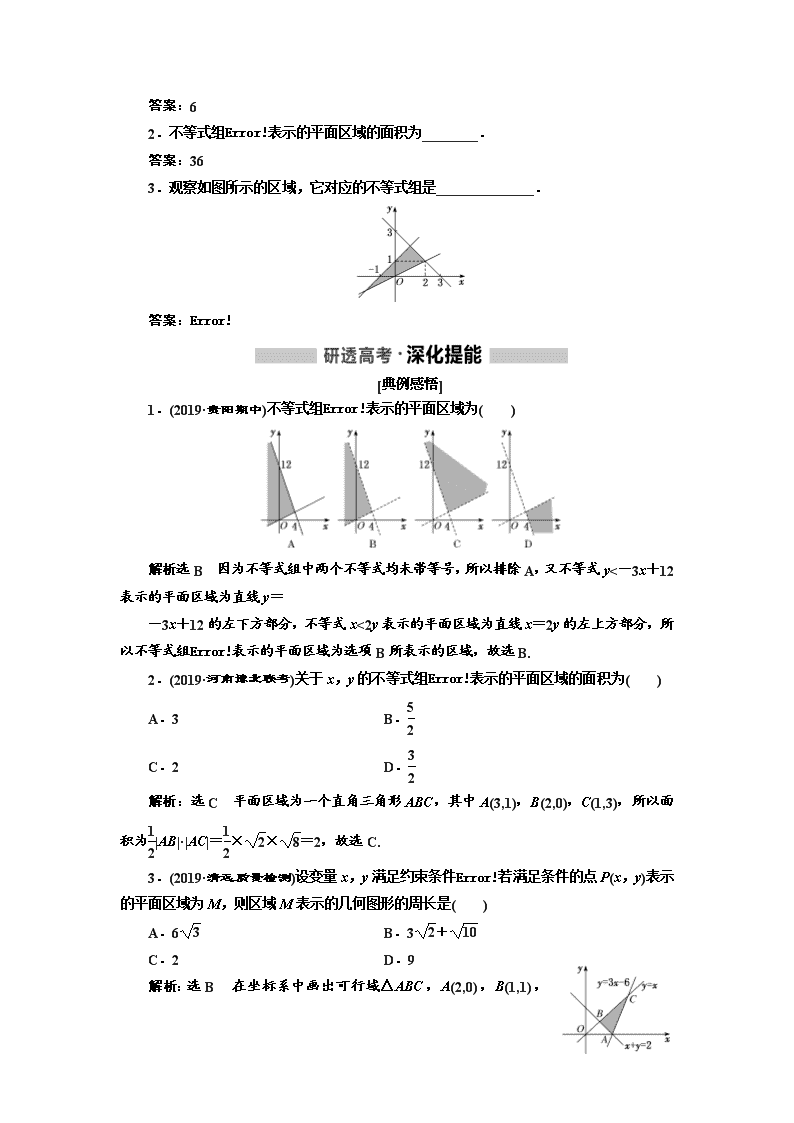
第二节 二元一次不等式(组) 与简单的线性 规划问题 1.会从实际情境中抽象出二元一次不等式组． 2.了解二元一次不等式的几何意义，能用平面 区域表示二元一次不等式组． 3.会从实际情境中抽象出一些简单的二元线 性规划问题，并能加以解决． 突破点一 二元一次不等式(组)表示的平面区域 [基本知识] 1．二元一次不等式(组)表示的平面区域 不等式 表示区域 Ax＋By＋C＞0 直线 Ax＋By＋C＝0 某一侧的所 有点组成的平面区域 不包括边界直线 Ax＋By＋C≥0 包括边界直线 不等式组 各个不等式所表示平面区域的公共部分 2.确定二元一次不等式(组)表示平面区域的步骤 以上简称为“直线定界，特殊点定域”． [基本能力] 一、判断题(对的打“√”，错的打“×”) (1)不等式 Ax＋By＋C>0 表示的平面区域一定在直线 Ax＋By＋C＝0 的上方．( ) (2)不等式 x2－y2<0 表示的平面区域是一、三象限角的平分线和二、四象限角的平分线 围成的含有 y 轴的两块区域．( ) 答案：(1)× (2)√ 二、填空题 1．在平面直角坐标系 xOy 中，若点 P(m,1)到直线 4x－3y－1＝0 的距离为 4，且点 P(m,1) 在不等式 2x＋y≥3 表示的平面区域内，则 m＝________. 答案：6 2．不等式组 x－y＋6≥0， x＋y≥0， x≤3 表示的平面区域的面积为________． 答案：36 3．观察如图所示的区域，它对应的不等式组是______________． 答案： x－y＋1≥0， x－2y≤0， x＋y－3≤0 [典例感悟] 1．(2019·贵阳期中)不等式组 y<－3x＋12， x<2y 表示的平面区域为( ) 解析：选 B 因为不等式组中两个不等式均未带等号，所以排除 A，又不等式 y<－3x ＋12 表示的平面区域为直线 y＝ －3x＋12 的左下方部分，不等式 x<2y 表示的平面区域为直线 x＝2y 的左上方部分，所 以不等式组 y<－3x＋12， x<2y 表示的平面区域为选项 B 所表示的区域，故选 B. 2．(2019·河南豫北联考)关于 x，y 的不等式组 3x＋y－6≥0， x－y－2≤0， x＋y－4≤0 表示的平面区域的面 积为( ) A．3 B．5 2 C．2 D．3 2 解析：选 C 平面区域为一个直角三角形 ABC，其中 A(3,1)，B(2,0)，C(1,3)，所以面 积为1 2|AB|·|AC|＝1 2 × 2× 8＝2，故选 C. 3．(2019·清远质量检测)设变量 x，y 满足约束条件 y≤x， x＋y≥2， y≥3x－6， 若满足条件的点 P(x， y)表示的平面区域为 M，则区域 M 表示的几何图形的周长是( ) A．6 3 B．3 2＋ 10 C．2 D．9 解析：选 B 在坐标系中画出可行域△ABC，A(2,0)，B(1,1)，C(3,3)， 用两点间距离公式可求得 AB＝ 2，AC＝ 10，BC＝2 2，则周长为 3 2 ＋ 10，故选 B. [方法技巧] 解决求平面区域面积问题的方法步骤 (1)画出不等式组表示的平面区域； (2)判断平面区域的形状，并求得直线的交点坐标、图形的边长、相关线段的长(三角形 的高、四边形的高)等，若为规则图形则利用图形的面积公式求解；若为不规则图形则利用 割补法求解． [提醒] 求面积时应考虑圆、平行四边形等图形的对称性． 突破点二 简单的线性规划问题 [基本知识] 1．线性规划中的基本概念 名称 意义 约束条件 由变量 x，y 组成的不等式(组) 线性约束 条件 由 x，y 的一次不等式(或方程)组成的不等式(组) 目标函数 关于 x，y 的函数解析式，如 z＝2x＋3y 等 线性目标 函数 关于 x，y 的一次函数解析式 可行解 满足线性约束条件的解(x，y) 可行域 所有可行解组成的集合 最优解 使目标函数取得最大值或最小值的可行解 线性规划 问题 在线性约束条件下求线性目标函数的最大值或最小值问题 2.简单线性规划问题的图解法 在确定线性约束条件和线性目标函数的前提下，用图解法求最优解的步骤概括为“画、 移、求、答”．即 [提醒] 求线性目标函数最值应注意的问题 求二元一次函数 z＝ax＋by(ab≠0)的最值，将函数 z＝ax＋by 转化为直线的斜截式：y ＝－a bx＋z b ，通过求直线的截距z b 的最值间接求出 z 的最值，应注意以下两点： (1)若 b>0，则截距z b 取最大值时，z 也取最大值；截距z b 取最小值时，z 也取最小值． (2)若 b<0，则截距z b 取最大值时，z 取最小值；截距z b 取最小值时，z 取最大值． [基本能力] 一、判断题(对的打“√”，错的打“×”) (1)线性目标函数的最优解可能不唯一．( ) (2)目标函数 z＝ax＋by(b≠0)中，z 的几何意义是直线 ax＋by－z＝0 在 y 轴上的截 距．( ) 答案：(1)√ (2)× 二、填空题 1．若实数 x，y 满足 x－y＋1≥0， x＋y≥0， x≤0， 则 2x＋y 的最小值为________． 答案：－1 2 2．(2018·全国卷Ⅱ)若 x，y 满足约束条件 x＋2y－5≥0， x－2y＋3≥0， x－5≤0， 则 z＝x＋y 的最大值为________． 答案：9 3．(2019·北京朝阳区模拟)若实数 x，y 满足 x－y＋1≤0， x≤0， 则 x2＋y2 的最小值是 ________． 答案：1 2 [全析考法] 考法一 线性目标函数的最值 [例 1] (1)(2018·全国卷Ⅰ)若 x，y 满足约束条件 x－2y－2≤0， x－y＋1≥0， y≤0， 则 z＝3x＋2y 的最 大值为________． (2)(2018·北京高考)若 x，y 满足 x＋1≤y≤2x，则 2y－x 的最小值是________． [解析] (1)作出满足约束条件的可行域如图中阴影部分所示． 由 z＝3x＋2y，得 y＝－3 2x＋z 2. 作直线 l0：y＝－3 2x. 平移直线 l0，当直线 y＝－3 2x＋z 2 过点(2,0)时， z 取最大值，zmax＝3×2＋2×0＝6. (2)由条件得 x＋1≤y， y≤2x， 即 x－y＋1≤0， 2x－y≥0， 作出不等式组所表示 的可行域如图中阴影部分所示． 设 z＝2y－x，即 y＝1 2x＋1 2z， 作直线 l0：y＝1 2x 并向上平移，显然当 l0 过点 A(1,2)时，z 取得最小 值，zmin＝2×2－1＝3. [答案] (1)6 (2)3 [方法技巧] 求解线性目标函数最值的常用方法 线性目标函数的最优解一般在平面区域的顶点或边界处取得，所以对于一般的线性规 划问题，若可行域是一个封闭的图形，我们可以直接解出可行域的顶点，然后将坐标代入 目标函数求出相应的数值，从而确定目标函数的最值；若可行域不是封闭图形还是需要借 助截距的几何意义来求最值． 考法二 非线性目标函数的最值 [例 2] (1)(2019·江西五市联考)已知实数 x，y 满足不等式组 x≥1， y≥2， x＋y≤4， 若点 P(2a ＋b,3a－b)在该不等式组所表示的平面区域内，则b＋2 a－1 的取值范围是( ) A．[－12，－7] B． －7，－9 2 C. －12，－9 2 D．[－12，－2] (2)(2019·唐山模拟)设实数 x，y 满足约束条件 x－2y－5≤0， x＋y－4≤0， 3x＋y－10≥0， 则 z＝x2＋y2 的最小 值为________． [解析] (1)因为点 P(2a＋b,3a－b)在不等式组 x≥1， y≥2， x＋y≤4 所表示的平面区域内， 所以 2a＋b≥1， 3a－b≥2， 2a＋b＋3a－b≤4， 即 2a＋b≥1， 3a－b≥2， 5a≤4， 其表示的平面区域是以 A 4 5 ，－3 5 ，B 4 5 ，2 5 ，C3 5 ，－1 5 为顶点的三 角形区域(包括边界)． b＋2 a－1 可看作是可行域内的点与点 M(1，－2)连线的斜率， 所以 kMB≤b＋2 a－1 ≤kMC，即－12≤b＋2 a－1 ≤－9 2. (2)作出不等式组表示的平面区域，如图所示． 因为 z＝x2＋y2 表示区域内的点到原点距离的平方， 由图知，当区域内的点与原点的连线与直线 3x＋y－10＝0 垂直时， z＝x2＋y2 取得最小值， 所以 zmin＝ |3×0＋0－10| 32＋12 2＝10，垂足为点(3,1)，在平面区域内，所以 z＝x2＋y2 的最 小值为 10. [答案] (1)C (2)10 [方法技巧] 非线性目标函数最值问题的常见类型及求法 距离平方 型 目标函数为 z＝(x－a)2＋(y－b)2 时，可转化为可行域内的点(x，y)与点(a，b)之 间的距离的平方求解 斜率型 对形如 z＝ay＋b cx＋d (ac≠0)型的目标函数，可利用斜率的几何意义来求最值，即先 变形为z＝ a c· y－ －b a x－ －d c 的形式，将问题化为求可行域内的点(x，y)与点 －d c ，－b a 连线的斜率的a c 倍的取值范围、最值等 点到直线 距离型 对形如 z＝|Ax＋By＋C|型的目标函数，可先变形为 z＝ A2＋B2·|Ax＋By＋C| A2＋B2 的 形式，将问题化为求可行域内的点(x，y)到直线Ax＋By＋C＝0的距离的 A2＋B2 倍的最值 考法三 线性规划中的参数问题 [例 3] (1)(2019·合肥质检)已知实数 x，y 满足不等式组 －3≤3x－y≤－1， －1≤x＋y≤1， 若 z＝ax ＋y 有最大值5 2 ，则 a 的值为( ) A．2 B．5 2 C．－2 D．－5 2 (2)(2019·淮北月考)若实数 x，y 满足约束条件 x＋y≥1， x－y≥－1， 3x－y≤3， 目标函数 z＝ax＋2y 仅 在点(1,0)处取得最小值，则实数 a 的取值范围是( ) A．[－6,2] B．(－6,2) C．[－3,1] D．(－3,1) [解析] (1)不等式组 －3≤3x－y≤－1， －1≤x＋y≤1 所表示的平面区域如图 中阴影部分所示．z＝ax＋y 有最大值5 2 ，即直线 y＝－ax＋z 在 y 轴上的截 距有最大值5 2 ，由图可知当直线 y＝－ax＋z 经过点 A 时，z 取得最大值5 2 ，由 3x－y＝－3， x＋y＝1， 解得 x＝－1 2 ， y＝3 2 ， 所以 A －1 2 ，3 2 ，代入 ax＋y＝5 2 ，得 a＝－2.故选 C. (2)作出约束条件所表示的平面区域，如图所示．将 z＝ax＋2y 化 成 y＝－a 2x＋z 2 ，当－1<－a 2<3 时，直线 y＝－a 2x＋z 2 的纵截距仅在点(1,0) 处取得最小值，即目标函数 z＝ax＋2y 在点(1,0)处取得最小值，解得 －60， 3x＋y<3， x＋y>a 表示的平面区域是一个三角形 区域(不包括边界)，则实数 a 的取值范围是( ) A. －∞，3 4 B． 3 4 ，＋∞ C. －∞，3 2 D． 3 2 ，＋∞ 解析：选 C 作出不等式组表示的可行域如图中阴影部分所示， 要使可行域为三角形区域(不包括边界)，则需点 A 在直线 x＋y＝a 的右上方． 由 x－y＝0， 3x＋y＝3 可得 A 3 4 ，3 4 ，所以3 4 ＋3 4>a，即 a<3 2.故选 C. 6．(2019·郑州模拟)已知直线 y＝k(x＋1)与不等式组 x＋y－4≤0， 3x－y≥0， x>0，y>0 表示的平面区域 有公共点，则 k 的取值范围为( ) A．[0，＋∞) B． 0，3 2 C. 0，3 2 D． 3 2 ，＋∞ 解析：选 C 不等式组表示的可行域如图中阴影部分所示(不包括直线 y＝0)，直线 y＝ k(x＋1)过定点(－1,0)，由 x＋y－4＝0， 3x－y＝0， 解得 x＝1， y＝3， 过点(－1,0)与(1,3) 的直线的斜率是3 2 ，根据题意可知 01 2 时，直线过点 B 时，z 取得 最大值 5，不成立，舍去；当 0

查看更多