数学卷·2018届河北省保定市博野中学高二上学期期中数学试卷（文科）（解析版）

数学卷·2018届河北省保定市博野中学高二上学期期中数学试卷（文科）（解析版）

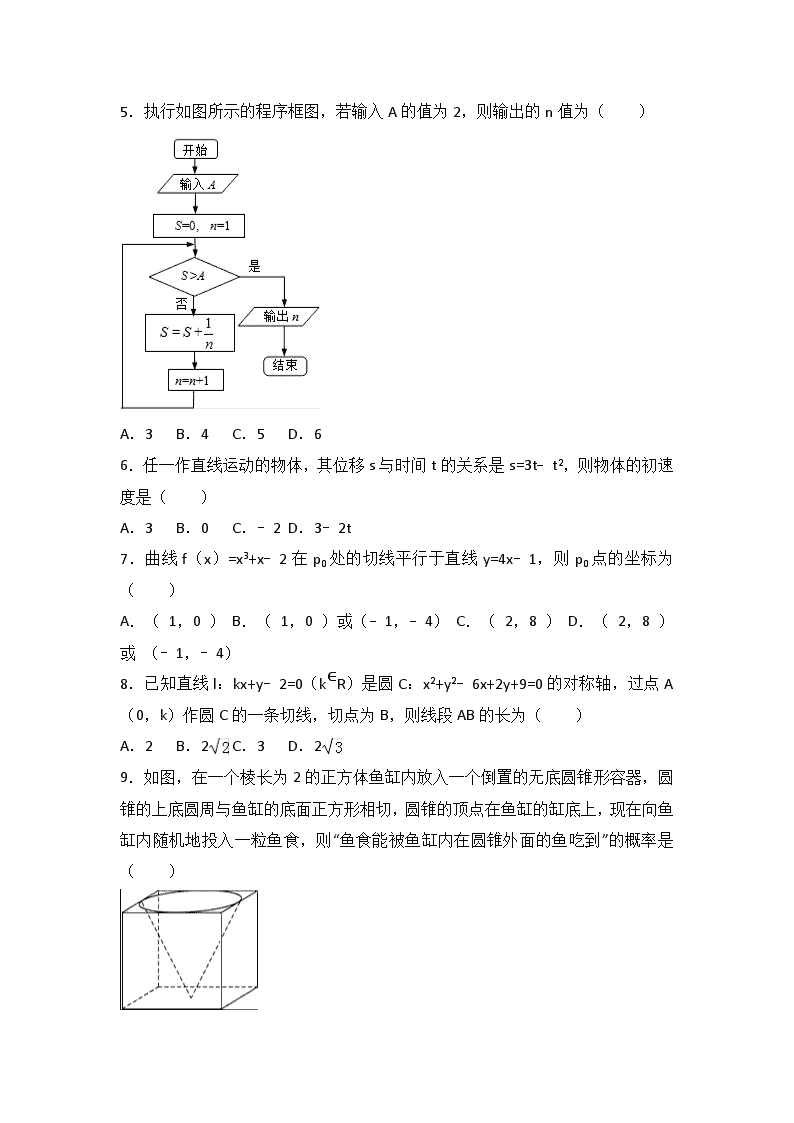
‎2016-2017学年河北省保定市博野中学高二（上）期中数学试卷（文科）‎ ‎　‎ 一、选择题（共12道小题，每小题5分，共60分）‎ ‎1．设曲线y=f（x）在某点处的导数值为0，则过曲线上该点的切线（　　）‎ A．垂直于x轴 B．垂直于y轴 C．既不垂直于x轴也不垂直于y轴 D．方向不能确定 ‎2．下列命题正确的个数是（　　）①已知p：∃x∈R，方程ax2﹣2x+a=0有正实根，则￢p：∀a∈R，方程ax2﹣2x+a=0有负实根 ‎②∃x∈R，x＞0‎ ‎③至少有一个整数，它既不是2的倍数，也不是3的倍数．‎ A．0 B．1 C．2 D．3‎ ‎3．如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图，现已知年龄 在[30，35），[35，40），[40，45]的上网人数呈现递减的等差数列，则年龄在[35，40）的频（　　）‎ A．0.04 B．0.06 C．0.2 D．0.3‎ ‎4．下列存在性命题中假命题的个数是（　　）‎ ‎①有的实数是无限不循环小数；‎ ‎②有些三角形不是等边三角形；‎ ‎③有的平行四边形是正方形．‎ A．0个 B．1个 C．2个 D．3个 ‎5．执行如图所示的程序框图，若输入A的值为2，则输出的n值为（　　）‎ A．3 B．4 C．5 D．6‎ ‎6．任一作直线运动的物体，其位移s与时间t的关系是s=3t﹣t2，则物体的初速度是（　　）‎ A．3 B．0 C．﹣2 D．3﹣2t ‎7．曲线f（x）=x3+x﹣2在p0处的切线平行于直线y=4x﹣1，则p0点的坐标为（　　）‎ A．（ 1，0 ） B．（ 1，0 ）或（﹣1，﹣4） C．（ 2，8 ） D．（ 2，8 ）或 （﹣1，﹣4）‎ ‎8．已知直线l：kx+y﹣2=0（k∈R）是圆C：x2+y2﹣6x+2y+9=0的对称轴，过点A（0，k）作圆C的一条切线，切点为B，则线段AB的长为（　　）‎ A．2 B．2 C．3 D．2‎ ‎9．如图，在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的上底圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是（　　）‎ A．1﹣ B． C． D．1﹣‎ ‎10．椭圆mx2+ny2=1与直线x+y﹣1=0相交于A，B两点，过AB中点M与坐标原点的直线的斜率为，则的值为（　　）‎ A． B． C．1 D．2‎ ‎11．已知双曲线C：﹣=1（a＞0，b＞0）的渐近线方程为y=±x，且其右焦点为（5，0），则双曲线C的方程为（　　）‎ A． B． C． D．‎ ‎12．过抛物线y2=2px（p＞0）的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点，则的值等于（　　）‎ A．5 B．4 C．3 D．2‎ ‎　‎ 二、填空题 ‎13．f′（x）是的导函数，则f′（﹣1）的值是 　　．‎ ‎14．命题“若a＞b，则2a＞2b﹣1”的否命题为　　．‎ ‎15．已知双曲线C：﹣=1的左、右焦点分别是F1，F2，正三角形AF1F2的一边AF1与双曲线左支交于点B，且=4，则双曲线C的离心率的值是　　．‎ ‎16．设椭圆C： +=1（a＞b＞0）的左、右焦点为F1，F2，过点F1的直线与椭圆C相交于A，B两点，若=，∠AF2B=90°，则椭圆C的离心率是　　．‎ ‎　‎ 三、解答题（共70分）‎ ‎17．（10分）已知p：方程x2+mx+1=0有两个不等的负根；q：方程4x2+4（m﹣2）x+1=0无实根，若“p或q”真“p且q”为假，求m的取值范围．‎ ‎18．（12分）已知椭圆C： +=1（a＞0，b＞0）的离心率为，A（a，0），B（0，b），O（0，0），△OAB的面积为1．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）设P是椭圆C上一点，直线PA与y轴交于点M，直线PB与x轴交于点N．求证：|AN|•|BM|为定值．‎ ‎19．（12分）我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．‎ ‎（Ⅰ）求直方图中a的值；‎ ‎（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；‎ ‎（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值，并说明理由．‎ ‎20．（12分）已知函数f（x）=x3+ax2+bx+c在x=﹣与x=1时都取得极值．‎ ‎（1）求a、b的值与函数f（x）的单调区间；‎ ‎（2）若对x∈[﹣1，2]，不等式f（x）＜c2恒成立，求c的取值范围．‎ ‎21．（12分）已知椭圆C： +=1过点A（2，0），B（0，1）两点．‎ ‎（1）求椭圆C的方程及离心率；‎ ‎（2）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值．‎ ‎22．（12分）已知函数f（x）=x2+lnx．‎ ‎（1）求函数f（x）在[1，e]上的最大值和最小值；‎ ‎（2）求证：当x∈（1，+∞）时，函数f（x）的图象在g（x）=x3+x2的下方．‎ ‎　‎ ‎2016-2017学年河北省保定市博野中学高二（上）期中数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题（共12道小题，每小题5分，共60分）‎ ‎1．设曲线y=f（x）在某点处的导数值为0，则过曲线上该点的切线（　　）‎ A．垂直于x轴 B．垂直于y轴 C．既不垂直于x轴也不垂直于y轴 D．方向不能确定 ‎【考点】导数的几何意义．‎ ‎【分析】曲线y=f（x）在某点处的导数值为0，可得切线的斜率为0，即可得出结论．‎ ‎【解答】解：∵曲线y=f（x）在某点处的导数值为0，‎ ‎∴切线的斜率为0，‎ 故选B．‎ ‎【点评】本题考查了导数的几何意义的应用，属于基础题．‎ ‎　‎ ‎2．下列命题正确的个数是（　　）①已知p：∃x∈R，方程ax2﹣2x+a=0有正实根，则￢p：∀a∈R，方程ax2﹣2x+a=0有负实根 ‎②∃x∈R，x＞0‎ ‎③至少有一个整数，它既不是2的倍数，也不是3的倍数．‎ A．0 B．1 C．2 D．3‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】①，命题“∃a∈R，方程ax2﹣2x+a=0有正实根”的否定是“∀a∈R，方程方程ax2﹣2x+a=0无正实根”； ‎ ‎②，∃x∈R，x＞0；‎ ‎③，整数5，它既不是2的倍数，也不是3的倍数．‎ ‎【解答】解：对于①，已知p：∃x∈R，方程ax2﹣2x+a=0有正实根，则￢p：∀a∈R，方程ax2﹣2x+a=0无正实根，故错；‎ 对于②，∃x∈R，x＞0，故正确；‎ 对于③，整数5，它既不是2的倍数，也不是3的倍数，故正确．‎ 故选：C ‎【点评】本题考查了命题真假的判定，属于基础题．‎ ‎　‎ ‎3．如图是某居民小区年龄在20岁到45岁的居民上网情况的频率分布直方图，现已知年龄 在[30，35），[35，40），[40，45]的上网人数呈现递减的等差数列，则年龄在[35，40）的频（　　）‎ A．0.04 B．0.06 C．0.2 D．0.3‎ ‎【考点】频率分布直方图．‎ ‎【分析】根据题意，结合频率、频数与样本容量的关系，利用等差数列的性质，即可求出答案．‎ ‎【解答】解：根据题意，得；‎ 年龄在[30，45]的上网人数的频率为 ‎1﹣（0.01+0.07）×5=0.6，‎ ‎∵年龄在[30，35），[35，40），[40，45]的上网人数呈现递减的等差数列，‎ ‎∴他们对应的频率也呈递减的等差数列，‎ ‎∴年龄在[35，40）的频率为 ‎×0.6=0.2．‎ 故选：C．‎ ‎【点评】‎ 本题考查了频率、频数与样本容量的关系，也考查了等差数列的应用问题，是基础题目．‎ ‎　‎ ‎4．下列存在性命题中假命题的个数是（　　）‎ ‎①有的实数是无限不循环小数；‎ ‎②有些三角形不是等边三角形；‎ ‎③有的平行四边形是正方形．‎ A．0个 B．1个 C．2个 D．3个 ‎【考点】命题的真假判断与应用．‎ ‎【分析】①，实数是无限不循环小数；‎ ‎②，直角三角形三角形不是等边三角形；‎ ‎③，显然正确．‎ ‎【解答】解：对于①，实数是无限不循环小数，故正确；‎ 对于②，直角三角形三角形不是等边三角形，故正确；‎ 对于③，显然正确．‎ 故选：A．‎ ‎【点评】本题考查了命题真假的判定，属于基础题．‎ ‎　‎ ‎5．执行如图所示的程序框图，若输入A的值为2，则输出的n值为（　　）‎ A．3 B．4 C．5 D．6‎ ‎【考点】程序框图．‎ ‎【分析】根据输入A的值，然后根据S进行判定是否满足条件S＞2，若不满足条件执行循环体，依此类推，一旦满足条件S＞2，退出循环体，输出n的值为5．‎ ‎【解答】解：模拟执行程序，可得 A=2，S=0，n=1‎ 不满足条件S＞2，执行循环体，S=1，n=2‎ 不满足条件S＞2，执行循环体，S=，n=3‎ 不满足条件S＞2，执行循环体，S=，n=4‎ 不满足条件S＞2，执行循环体，S=，n=5‎ 满足条件S＞2，退出循环，输出n的值为5．‎ 故选：C．‎ ‎【点评】本题主要考查了当型循环结构，循环结构有两种形式：当型循环结构和直到型循环结构，当型循环是先判断后循环，直到型循环是先循环后判断，属于基础题．‎ ‎　‎ ‎6．任一作直线运动的物体，其位移s与时间t的关系是s=3t﹣t2，则物体的初速度是（　　）‎ A．3 B．0 C．﹣2 D．3﹣2t ‎【考点】变化的快慢与变化率．‎ ‎【分析】求函数的导数，令x=0即可得到结论．‎ ‎【解答】解：∵位移s与时间t的关系是s=s（t）=3t﹣t2，‎ ‎∴s′（t）=3﹣2t，‎ ‎∴s′（0）=3，‎ 故物体的初速度3，‎ 故选：A．‎ ‎【点评】本题主要考查导数的基本运算，比较基础．‎ ‎　‎ ‎7．曲线f（x）=x3+x﹣2在p0处的切线平行于直线y=4x﹣1，则p0点的坐标为（　　）‎ A．（ 1，0 ） B．（ 1，0 ）或（﹣1，﹣4） C．（ 2，8 ） D．（ 2，8 ）或 （﹣1，﹣4）‎ ‎【考点】利用导数研究曲线上某点切线方程．‎ ‎【分析】由求导公式和法则求出函数的导数，由切线的斜率求出切点的横坐标，再代入函数解析式求出纵坐标．‎ ‎【解答】解：由y=x3+x﹣2，得y′=3x2+1，‎ ‎∵切线平行于直线y=4x﹣1，‎ ‎∴3x2+1=4，解之得x=±1，‎ 当x=1时，y=0；当x=﹣1时，y=﹣4．‎ ‎∴切点P0的坐标为（1，0）和（﹣1，﹣4），‎ 故选：B．‎ ‎【点评】本题考查了导数的几何意义，在切点处的导数值是切线斜率，考查运算能力，属于基础题．‎ ‎　‎ ‎8．已知直线l：kx+y﹣2=0（k∈R）是圆C：x2+y2﹣6x+2y+9=0的对称轴，过点A（0，k）作圆C的一条切线，切点为B，则线段AB的长为（　　）‎ A．2 B．2 C．3 D．2‎ ‎【考点】圆的切线方程．‎ ‎【分析】利用配方法求出圆的标准方程可得圆心和半径，由直线l：kx+y﹣2=0经过圆C的圆心（3，﹣1），求得k的值，可得点A的坐标，再利用直线和圆相切的性质求得AB的值．‎ ‎【解答】解：由圆C：x2+y2﹣6x+2y+9=0得，（x﹣3）2+（y+1）2=1，‎ 表示以C（3，﹣1）为圆心、半径等于1的圆．‎ 由题意可得，直线l：kx+y﹣2=0经过圆C的圆心（3，﹣1），‎ 故有3k﹣1﹣2=0，得k=1，则点A（0，1），‎ 即|AC|=．‎ 则线段AB=．‎ 故选：D．‎ ‎【点评】‎ 本题考查圆的切线长的求法，解题时要注意圆的标准方程，直线和圆相切的性质的合理运用，属于中档题．‎ ‎　‎ ‎9．如图，在一个棱长为2的正方体鱼缸内放入一个倒置的无底圆锥形容器，圆锥的上底圆周与鱼缸的底面正方形相切，圆锥的顶点在鱼缸的缸底上，现在向鱼缸内随机地投入一粒鱼食，则“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是（　　）‎ A．1﹣ B． C． D．1﹣‎ ‎【考点】几何概型．‎ ‎【分析】由题意，直接看顶部形状，及正方形内切一个圆，正方形面积为4，圆为π，即可求出“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率．‎ ‎【解答】解：由题意，正方形的体积为23=8．倒立的圆锥的体积为：π•2，‎ 所以“鱼食能被鱼缸内在圆锥外面的鱼吃到”的概率是1﹣=1﹣，‎ 故选：D．‎ ‎【点评】本题考查概率的计算，考查学生分析解决问题的能力，属于中档题．‎ ‎　‎ ‎10．椭圆mx2+ny2=1与直线x+y﹣1=0相交于A，B两点，过AB中点M与坐标原点的直线的斜率为，则的值为（　　）‎ A． B． C．1 D．2‎ ‎【考点】直线与圆锥曲线的关系．‎ ‎【分析】（法一）设A（x1，y1），B（x2，y2），M（x0，y0）由①，②及M，N在椭圆上，可得利用点差法进行求解 ‎（法二）A（x1，y1），B（x2，y2），M（x0，y0），联立方程．，利用方程的根与系数的关系可求x1+x2，进而可求y1+y2=2﹣（x1+x2），由中点坐标公式可得，，，由题意可知，从而可求 ‎【解答】解：设A（x1，y1），B（x2，y2），M（x0，y0），‎ ‎∴①，‎ kAB=②，‎ 由AB的中点为M可得x1+x2=2x0，y1+y2=2y0‎ 由A，B在椭圆上，可得，‎ 两式相减可得m（x1﹣x2）（x1+x2）+n（y1﹣y2）（y1+y2）=0③，‎ 把①②代入③可得m（x1﹣x2）•2x0﹣n（x1﹣x2）•2y0=0③，‎ 整理可得 故选A ‎（法二）设A（x1，y1），B（x2，y2），M（x0，y0）‎ 联立方程可得（m+n）x2﹣2nx++n﹣1=0‎ ‎∴x1+x2=，y1+y2=2﹣（x1+x2）=‎ 由中点坐标公式可得， =， =‎ ‎∵M与坐标原点的直线的斜率为 ‎∴=‎ 故选A ‎【点评】题主要考查了直线与椭圆相交的位置关系，在涉及到与弦的斜率及中点有关时的常用方法有两个：①联立直线与椭圆，根据方程求解；②利用“点差法”，而第二种方法可以简化运算，注意应用 ‎　‎ ‎11．已知双曲线C：﹣=1（a＞0，b＞0）的渐近线方程为y=±x，且其右焦点为（5，0），则双曲线C的方程为（　　）‎ A． B． C． D．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】利用已知条件列出方程，求解即可．‎ ‎【解答】解：双曲线C：﹣=1（a＞0，b＞0）的渐近线方程为y=±x，‎ 可得=；其右焦点为（5，0），可得c=5，又c2=a2+b2，‎ 解得a=4，b=3，‎ 则双曲线C的方程为：．‎ 故选：B．‎ ‎【点评】本题考查双曲线方程的求法，双曲线的简单性质的应用，是基础题．‎ ‎　‎ ‎12．过抛物线y2=2px（p＞0）的焦点F且倾斜角为60°的直线l与抛物线在第一、四象限分别交于A、B两点，则的值等于（　　）‎ A．5 B．4 C．3 D．2‎ ‎【考点】直线的倾斜角；抛物线的简单性质．‎ ‎【分析】设出A、B坐标，利用焦半径公式求出|AB|，结合，求出A、B的坐标，然后求其比值．‎ ‎【解答】解：设A（x1，y1），B（x2，y2），‎ ‎，，‎ 又，可得，‎ 则，‎ 故选C．‎ ‎【点评】本题考查直线的倾斜角，抛物线的简单性质，考查学生分析问题解决问题的能力，是基础题．‎ ‎　‎ 二、填空题 ‎13．f′（x）是的导函数，则f′（﹣1）的值是 　3　．‎ ‎【考点】函数的值；导数的运算．‎ ‎【分析】利用求导法则（xn）′=nxn﹣1，求出f（x）的导函数，然后把x等于﹣1代入导函数中求出f′（﹣1）即可．‎ ‎【解答】解：f′（x）=x2+2，把x=﹣1代入f′（x）得：f′（﹣1）=1+2=3‎ 故答案为：3‎ ‎【点评】此题考查学生灵活运用求导法则求函数的导函数，会求自变量对应的导函数的函数值，是一道基础题．‎ ‎　‎ ‎14．命题“若a＞b，则2a＞2b﹣1”的否命题为　若a≤b，则2a≤2b﹣1　．‎ ‎【考点】命题的否定；四种命题．‎ ‎【分析】写出一个命题的否命题的关键是正确找出原命题的条件和结论．‎ ‎【解答】解：命题“若a＞b，则2a＞2b﹣1”的否命题为“若a≤b，则2a≤2b﹣1”．‎ 故答案为若a≤b，则2a≤2b﹣1．‎ ‎【点评】本题主要考查了命题的否定，属基础题型，较简单．‎ ‎　‎ ‎15．已知双曲线C：﹣=1的左、右焦点分别是F1，F2，正三角形AF1F2的一边AF1与双曲线左支交于点B，且=4，则双曲线C的离心率的值是　‎ ‎　．‎ ‎【考点】双曲线的简单性质．‎ ‎【分析】求出F1（﹣c，0），A（0， c），设B（x，y），根据=4，可得x=﹣c，y=c，代入双曲线方程，即可得出结论．‎ ‎【解答】解：由题意，F1（﹣c，0），A（0， c），‎ 设B（x，y），则 ‎∵=4，‎ ‎∴（﹣c，﹣ c）=4（﹣c﹣x，﹣y），‎ ‎∴x=﹣c，y=c，‎ 代入双曲线方程，化简可得，9e4﹣28e2+16=0，‎ ‎∴e=．‎ 故答案为：．‎ ‎【点评】本题考查双曲线的几何性质，考查向量知识的运用，考查学生的计算能力，确定坐标之间的关系是关键．‎ ‎　‎ ‎16．设椭圆C： +=1（a＞b＞0）的左、右焦点为F1，F2，过点F1的直线与椭圆C相交于A，B两点，若=，∠AF2B=90°，则椭圆C的离心率是　　．‎ ‎【考点】椭圆的简单性质．‎ ‎【分析】由条件可设|BF1|=2t，|AF1|=3t，由椭圆的定义，可得|AF2|=2a﹣3t，|BF2|=2a﹣2t，运用勾股定理，可得t=a，求出cosB，△F1BF2中，运用余弦定理和离心率公式计算即可得到所求值．‎ ‎【解答】解：由=，可设|BF1|=2t，|AF1|=3t，‎ 由椭圆的定义，可得|AF2|=2a﹣3t，|BF2|=2a﹣2t，‎ 由∠AF2B=90°可得|AB|2=|AF2|2+|BF2|2，‎ 即有（5t）2=（2a﹣3t）2+（2a﹣2t）2，‎ 解得t=a，|AB|=a，|BF2|=a，‎ 在△ABF2中，cosB==，‎ 在△F1BF2中，cosB==，‎ 化简可得•=，‎ 即e2=，即为e=．‎ 故答案为：．‎ ‎【点评】本题考查椭圆的离心率的求法，注意运用椭圆的定义，三角形的勾股定理和余弦定理，考查向量共线定理，考查化简整理的运算能力，属于中档题．‎ ‎　‎ 三、解答题（共70分）‎ ‎17．（10分）（2016秋•郏县期中）已知p：方程x2+mx+1=0有两个不等的负根；q：方程4x2+4（m﹣2）x+1=0无实根，若“p或q”真“p且q”为假，求m的取值范围．‎ ‎【考点】命题的真假判断与应用．‎ ‎【分析】若“p或q”真“p且q”为假，命题p，q应一真一假，分类讨论，可得m的取值范围．‎ ‎【解答】解：若方程 x2+mx+1=0有两个不等的负根，‎ 则 ‎ 解得m＞2，‎ 若方程4x2+4（m﹣2）x+1=0无实根，则△=16（m﹣2）2﹣16＜0，‎ 解得：1＜m＜3‎ ‎∵“p或q”真“p且q”，‎ 因此，命题p，q应一真一假，‎ ‎∴或，‎ 解得：m∈（1，2]∪[3，+∞）．‎ ‎【点评】本题以命题的真假判断与应用为载体，考查了复合命题，二次方程根与系数的关系，难度中档．‎ ‎　‎ ‎18．（12分）（2016•北京）已知椭圆C： +=1（a＞0，b＞0）的离心率为，A（a，0），B（0，b），O（0，0），△OAB的面积为1．‎ ‎（Ⅰ）求椭圆C的方程；‎ ‎（Ⅱ）设P是椭圆C上一点，直线PA与y轴交于点M，直线PB与x轴交于点N．求证：|AN|•|BM|为定值．‎ ‎【考点】直线与椭圆的位置关系．‎ ‎【分析】（Ⅰ）运用椭圆的离心率公式和三角形的面积公式，结合a，b，c的关系，解方程可得a=2，b=1，进而得到椭圆方程；‎ ‎（Ⅱ）方法一、设椭圆上点P（x0，y0），可得x02+4y02=4，求出直线PA的方程，令x=0，求得y，|BM|；求出直线PB的方程，令y=0，可得x，|AN|，化简整理，即可得到|AN|•|BM|为定值4．‎ 方法二、设P（2cosθ，sinθ），（0≤θ＜2π），求出直线PA的方程，令x=0，求得y，|BM|；求出直线PB的方程，令y=0，可得x，|AN|，运用同角的平方关系，化简整理，即可得到|AN|•|BM|为定值4．‎ ‎【解答】解：（Ⅰ）由题意可得e==，‎ 又△OAB的面积为1，可得ab=1，‎ 且a2﹣b2=c2，‎ 解得a=2，b=1，c=，‎ 可得椭圆C的方程为+y2=1；‎ ‎（Ⅱ）证法一：设椭圆上点P（x0，y0），‎ 可得x02+4y02=4，‎ 直线PA：y=（x﹣2），令x=0，可得y=﹣，‎ 则|BM|=|1+|；‎ 直线PB：y=x+1，令y=0，可得x=﹣，‎ 则|AN|=|2+|．‎ 可得|AN|•|BM|=|2+|•|1+|‎ ‎=||=||‎ ‎=||=4，‎ 即有|AN|•|BM|为定值4．‎ 证法二：设P（2cosθ，sinθ），（0≤θ＜2π），‎ 直线PA：y=（x﹣2），令x=0，可得y=﹣，‎ 则|BM|=||；‎ 直线PB：y=x+1，令y=0，可得x=﹣，‎ 则|AN|=||．‎ 即有|AN|•|BM|=||•||‎ ‎=2||‎ ‎=2||=4．‎ 则|AN|•|BM|为定值4．‎ ‎【点评】本题考查椭圆的方程的求法，注意运用椭圆的离心率和基本量的关系，考查线段积的定值的求法，注意运用直线方程和点满足椭圆方程，考查化解在合理的运算能力，属于中档题．‎ ‎　‎ ‎19．（12分）（2016秋•博野县校级期中）我国是世界上严重缺水的国家，某市政府为了鼓励居民节约用水，计划调整居民生活用水收费方案，拟确定一个合理的月用水量标准x（吨），一位居民的月用水量不超过x的部分按平价收费，超出x的部分按议价收费．为了了解居民用水情况，通过抽样，获得了某年100位居民每人的月均用水量（单位：吨），将数据按照[0，0.5），[0.5，1），…，[4，4.5）分成9组，制成了如图所示的频率分布直方图．‎ ‎（Ⅰ）求直方图中a的值；‎ ‎（Ⅱ）设该市有30万居民，估计全市居民中月均用水量不低于3吨的人数，并说明理由；‎ ‎（Ⅲ）若该市政府希望使85%的居民每月的用水量不超过标准x（吨），估计x的值，并说明理由．‎ ‎【考点】用样本的数字特征估计总体的数字特征；频率分布直方图．‎ ‎【分析】（Ⅰ）根据各组的累积频率为1，构造方程，可得a值；‎ ‎（Ⅱ）由图可得月均用水量不低于3吨的频率，进而可估算出月均用水量不低于3吨的人数；‎ ‎（Ⅲ）由图可得月均用水量低于2.5吨的频率及月均用水量低于3吨的频率，进而可得x值．‎ ‎【解答】解：（Ⅰ）∵0.5×（0.08+0.16+0.4+0.52+0.12+0.08+0.04+2a）=1，‎ ‎∴a=0.3；‎ ‎（Ⅱ）由图可得月均用水量不低于3吨的频率为：0.5×（0.12+0.08+0.04）=0.12，‎ 由30×0.12=3.6得：全市居民中月均用水量不低于3吨的人数约为3.6万；‎ ‎（Ⅲ）由图可得月均用水量低于2.5吨的频率为：0.5×（0.08+0.16+0.3+0.4+0.52）=0.73＜85%；‎ 月均用水量低于3吨的频率为：0.5×（0.08+0.16+0.3+0.4+0.52+0.3）=0.88＞85%；‎ 则x=2.5+0.5×=2.9吨 ‎【点评】本题考查的知识点是频率分布直方图，用样本估计总体，难度不大，属于基础题．‎ ‎　‎ ‎20．（12分）（2006•江西）已知函数f（x）=x3+ax2+bx+c在x=﹣与x=1时都取得极值．‎ ‎（1）求a、b的值与函数f（x）的单调区间；‎ ‎（2）若对x∈[﹣1，2]，不等式f（x）＜c2恒成立，求c的取值范围．‎ ‎【考点】利用导数研究函数的极值；函数恒成立问题；利用导数研究函数的单调性．‎ ‎【分析】（1）求出f′（x），因为函数在x=﹣与x=1时都取得极值，所以得到f′（﹣）=0且f′（1）=0联立解得a与b的值，然后把a、b的值代入求得f（x）及f′（x），然后讨论导函数的正负得到函数的增减区间；‎ ‎（2）根据（1）函数的单调性，由于x∈[﹣1，2]恒成立求出函数的最大值值为f（2），代入求出最大值，然后令f（2）＜c2列出不等式，求出c的范围即可．‎ ‎【解答】解；（1）f（x）=x3+ax2+bx+c，f'（x）=3x2+2ax+b 由解得，‎ f'（x）=3x2﹣x﹣2=（3x+2）（x﹣1），函数f（x）的单调区间如下表：‎ x ‎（﹣∞，﹣）‎ ‎﹣‎ ‎（﹣，1）‎ ‎1‎ ‎（1，+∞）‎ f′（x）‎ ‎+‎ ‎0‎ ‎﹣‎ ‎0‎ ‎+‎ f（x）‎ ‎↑‎ 极大值 ‎↓‎ 极小值 ‎↑‎ 所以函数f（x）的递增区间是（﹣∞，﹣）和（1，+∞），递减区间是（﹣，1）．‎ ‎（2），‎ 当x=﹣时，f（x）=+c为极大值，而f（2）=2+c，所以f（2）=2+c为最大值．‎ 要使f（x）＜c2对x∈[﹣1，2]恒成立，须且只需c2＞f（2）=2+c．‎ 解得c＜﹣1或c＞2．‎ ‎【点评】考查学生利用导数研究函数极值的能力，利用导数研究函数单调性的能力，以及理解函数恒成立时所取到的条件．‎ ‎　‎ ‎21．（12分）（2016•北京）已知椭圆C： +=1过点A（2，0），B（0，1）两点．‎ ‎（1）求椭圆C的方程及离心率；‎ ‎（2）设P为第三象限内一点且在椭圆C上，直线PA与y轴交于点M，直线PB与x轴交于点N，求证：四边形ABNM的面积为定值．‎ ‎【考点】椭圆的标准方程；直线与椭圆的位置关系．‎ ‎【分析】（1）由题意可得a=2，b=1，则，则椭圆C的方程可求，离心率为e=；‎ ‎（2）设P（x0，y0），求出PA、PB所在直线方程，得到M，N的坐标，求得|AN|，|BM|．由，结合P在椭圆上求得四边形ABNM的面积为定值2．‎ ‎【解答】（1）解：∵椭圆C： +=1过点A（2，0），B（0，1）两点，‎ ‎∴a=2，b=1，则，‎ ‎∴椭圆C的方程为，离心率为e=；‎ ‎（2）证明：如图，‎ 设P（x0，y0），则，PA所在直线方程为y=，‎ 取x=0，得；‎ ‎，PB所在直线方程为，‎ 取y=0，得．‎ ‎∴|AN|=，‎ ‎|BM|=1﹣．‎ ‎∴=‎ ‎=﹣==‎ ‎=．‎ ‎∴四边形ABNM的面积为定值2．‎ ‎【点评】本题考查椭圆的标准方程，考查了椭圆的简单性质，考查计算能力与推理论证能力，是中档题．‎ ‎　‎ ‎22．（12分）（2013•西安校级一模）已知函数f（x）=x2+lnx．‎ ‎（1）求函数f（x）在[1，e]上的最大值和最小值；‎ ‎（2）求证：当x∈（1，+∞）时，函数f（x）的图象在g（x）=x3+x2的下方．‎ ‎【考点】利用导数求闭区间上函数的最值；导数在最大值、最小值问题中的应用．‎ ‎【分析】（1）求出导数f′（x），易判断x＞1时f′（x）的符号，从而可知f（x）的单调性，根据单调性可得函数的最值；‎ ‎（2）令F（x）=f（x）﹣g（x）=﹣+lnx，则只需证明F（x）＜0在（1，+∞）上恒成立，进而转化为F（x）的最大值小于0，利用导数可求得F（x）的最大值．‎ ‎【解答】（1）解：∵f（x）=x2+lnx，∴f′（x）=2x+，‎ ‎∵x＞1时，f′（x）＞0，‎ ‎∴f（x）在[1，e]上是增函数，‎ ‎∴f（x）的最小值是f（1）=1，最大值是f（e）=1+e2；‎ ‎（2）证明：令F（x）=f（x）﹣g（x）=﹣+lnx，‎ 则F′（x）=x﹣2x2+===‎