高中数学必修1示范教案（2_2 函数模型的应用举例 第2课时）

高中数学必修1示范教案（2_2 函数模型的应用举例 第2课时）

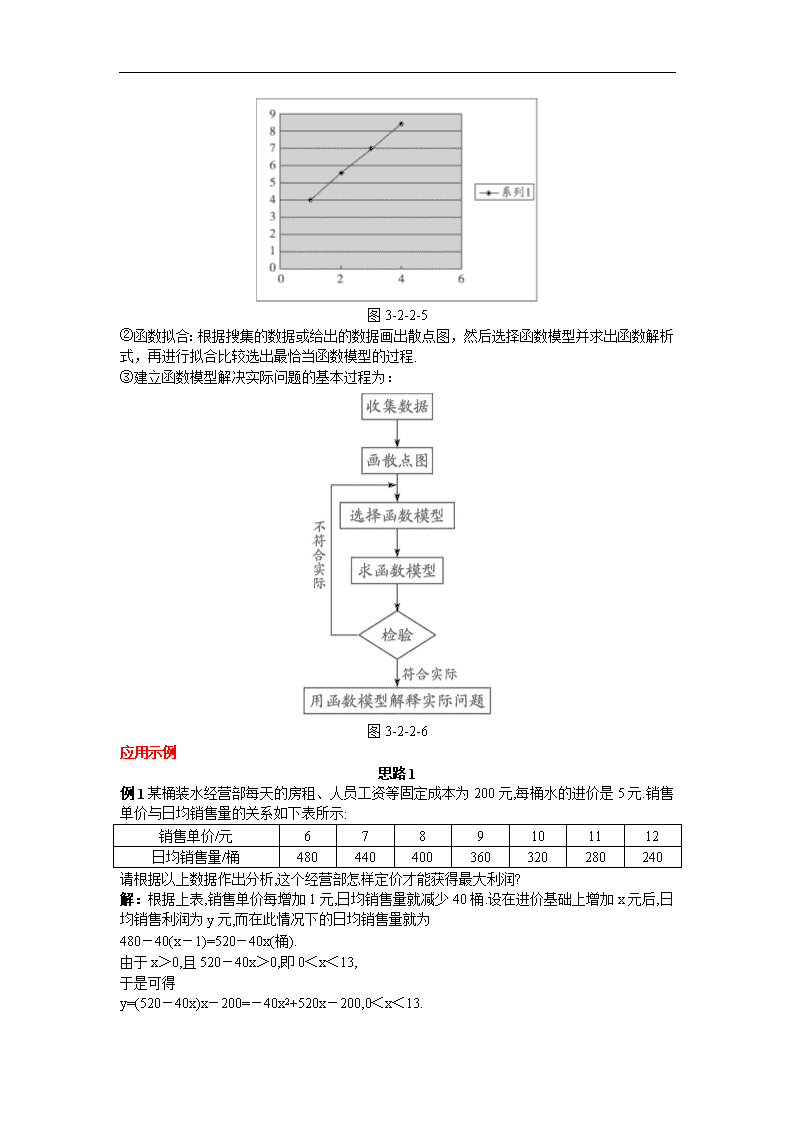
第2课时 函数模型的应用举例 导入新课 思路1.(事例导入)‎ 一辆汽车在水平的公路上匀加速行驶，初速度为v0,加速度为a,那么经过t小时它的速度为多少？在这t小时中经过的位移是多少？试写出它们函数解析式，它们分别属于那种函数模型？v=v0+at,s=v0t+at2,它们分别属于一次函数模型和二次函数模型.‎ 不仅在物理现象中用到函数模型，在其他现实生活中也经常用到函数模型，今天我们继续讨论函数模型的应用举例.‎ 思路2.(直接导入)‎ 前面我们学习了函数模型的应用，今天我们在巩固函数模型应用的基础上进一步讨论函数拟合问题.‎ 推进新课 新知探究 提出问题 ‎①我市某企业常年生产一种出口产品，根据需求预测：进入21世纪以来，前8年在正常情况下，该产品产量将平稳增长.已知2000年为第一年，头4年年产量f(x)(万件)如下表所示：‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ f(x)‎ ‎4.00‎ ‎5.58‎ ‎7.00‎ ‎8.44‎ ‎1°画出2000～2003年该企业年产量的散点图；建立一个能基本反映（误差小于0.1）这一时期该企业年产量发展变化的函数模型，并求之.‎ ‎2°2006年(即x＝7)因受到某外国对我国该产品反倾销的影响，年产量应减少30%，试根据所建立的函数模型，确定2006年的年产量应该约为多少？‎ ‎②什么是函数拟合？‎ ‎③总结建立函数模型解决实际问题的基本过程.‎ 讨论结果：①1°如图3-2-2-5，‎ 设f(x)＝ax＋b,代入（1，4）、（3，7）,得解得a=，b=.‎ ‎∴f(x)=x+.‎ 检验：f(2)＝5.5，|5.58-5.5|=0.08<0.1；‎ f(4)＝8.5，|8.44-8.5|=0.06<0.1.‎ ‎∴模型f(x)=x+能基本反映产量变化.‎ ‎2°f(7)＝13，13×70%＝9.1，2006年年产量应约为9.1万件.‎ 图3-2-2-5‎ ‎②函数拟合：根据搜集的数据或给出的数据画出散点图，然后选择函数模型并求出函数解析式，再进行拟合比较选出最恰当函数模型的过程.‎ ‎③建立函数模型解决实际问题的基本过程为：‎ 图3-2-2-6‎ 应用示例 思路1‎ 例1某桶装水经营部每天的房租、人员工资等固定成本为200元,每桶水的进价是5元.销售单价与日均销售量的关系如下表所示:‎ 销售单价/元 ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 日均销售量/桶 ‎480‎ ‎440‎ ‎400‎ ‎360‎ ‎320‎ ‎280‎ ‎240‎ 请根据以上数据作出分析,这个经营部怎样定价才能获得最大利润?‎ 解：根据上表,销售单价每增加1元,日均销售量就减少40桶.设在进价基础上增加x元后,日均销售利润为y元,而在此情况下的日均销售量就为 ‎480－40(x－1)=520－40x(桶).‎ 由于x＞0,且520－40x＞0,即0＜x＜13,‎ 于是可得 y=(520－40x)x－200=－40x2+520x－200,0＜x＜13.‎ 易知,当x=6.5时,y有最大值.‎ 所以,只需将销售单价定为11.5元,就可获得最大的利润.‎ 变式训练 某工厂现有80台机器，每台机器平均每天生产384件产品，现准备增加一批同类机器以提高生产总量，在试生产中发现，由于其他生产条件没变，因此每增加一台机器，每台机器平均每天将少生产4件产品．‎ ‎（1）如果增加x台机器，每天的生产总量为y件，请你写出y与x之间的关系式；‎ ‎（2）增加多少台机器，可以使每天的生产总量最大？最大生产总量是多少？‎ 解：（1）设在原来基础上增加x台，则每台生产数量为384-4x件，机器台数为80+x，‎ 由题意有y=(80+x)(384-4x).‎ ‎（2）整理得y=-4x2+64x+30 720，‎ 由y=-4x2+64x+30 720,得y=-4(x-8)2+30 976，‎ 所以增加8台机器每天生产的总量最大，最大生产总量为30 976件.‎ 点评：二次函数模型是现实生活中最常见数学模型.‎ 例2某地区不同身高的未成年男性的体重平均值如下表:‎ 身高∕cm ‎60‎ ‎70‎ ‎80‎ ‎90‎ ‎100‎ ‎110‎ ‎120‎ ‎130‎ ‎140‎ ‎150‎ ‎160‎ ‎170‎ 体重∕kg ‎6.13‎ ‎7.90‎ ‎9.99‎ ‎12.15‎ ‎15.02‎ ‎17.50‎ ‎20.92‎ ‎26.86‎ ‎31.11‎ ‎38.85‎ ‎47.25‎ ‎55.05‎ ‎（1）根据上表提供的数据，能否建立恰当的函数模型，使它能比较近似地反映这个地区未成年男性体重y kg与身高x cm的函数关系？试写出这个函数模型的解析式.‎ ‎(2)若体重超过相同身高男性体重的1.2倍为偏胖，低于0.8倍为偏瘦，那么这个地区一名身高为175cm，体重为78kg的在校男生的体重是否正常？‎ 活动：学生先思考或讨论，再回答.教师根据实际，可以提示引导：‎ 根据表的数据画出散点图.观察发现，这些点的连线是一条向上弯曲的曲线.根据这些点的分布情况，可以考虑用y=a·bx这一函数模型来近似刻画这个地区未成年男性体重y kg与身高x cm的函数关系.‎ 解：（1）以身高为横坐标，体重为纵坐标，画出散点图（图3-2-2-7）.根据点的分布特征，可以考虑用y=a·bx作为刻画这个地区未成年男性体重y kg与身高x cm关系的函数模型.‎ 如果取其中的两组数据（70，7.90）,(160,47.25),代入y=a·bx,得 用计算器算得a≈2,b≈1.02.‎ 这样，我们就得到一个函数模型：y=2×1.02x.‎ 将已知数据代入上述函数解析式，或作出上述函数的图象（图3-2-2-8），可以发现，这个函数模型与已知数据的拟合程度较好，这说明它能较好地反映这个地区未成年男性体重与身高的关系.‎ ‎(2)将x=175代入y=2×1.02x，得y=2×1.02175，‎ 由计算器算得y≈63.98.‎ 由于78÷63.98≈1.22>1.2,‎ 所以这个男生偏胖.‎ 图3-2-2-7 图3-2-2-8‎ 变式训练 九十年代，政府间气候变化专业委员会（IPCC）提供的一项报告指出：使全球气候逐年变暖的一个重要因素是人类在能源利用与森林砍伐中使CO2浓度增加.据测，1990年、1991年、1992年大气中的CO2浓度分别比1989年增加了1个可比单位、3个可比单位、6个可比单位.若用一个函数模拟九十年代中每年CO2浓度增加的可比单位数y与年份增加数x的关系，模拟函数可选用二次函数或函数y=a·bx+c（其中a、b、c为常数），且又知1994年大气中的CO2浓度比1989年增加了16个可比单位，请问用以上哪个函数作为模拟函数较好？‎ 解：(1)若以f(x)=px2+qx+r作模拟函数，‎ 则依题意得解得所以f(x)=x2+x.‎ ‎(2)若以g(x)=a·bx+c作模拟函数，则解得 所以g(x)=·()x-3.‎ ‎(3)利用f(x)、g(x)对1994年CO2浓度作估算，则其数值分别为：‎ f(5)=15可比单位，g(5)=17.25可比单位，‎ ‎∵|f(5)－16|<|g(5)－16|,‎ 故选f(x)=x2+x作为模拟函数与1994年的实际数据较为接近.‎ 思路2‎ 例1某自来水厂的蓄水池有400吨水,水厂每小时可向蓄水池中注水60吨,同时蓄水池又向居民小区不间断供水,t小时内供水总量为1206t吨,其中0≤t≤24.‎ ‎(1)从供水开始到第几小时,蓄水池中的存水量最少?最少水量是多少吨?‎ ‎(2)若蓄水池中水量少于80吨时,就会出现供水紧张现象,请问:在一天的24小时内,有几小时出现供水紧张现象?‎ 活动：学生先思考或讨论，再回答.教师根据实际，可以提示引导.‎ 思路分析：首先建立函数模型，利用函数模型解决实际问题.‎ 解：设供水t小时，水池中存水y吨，则 ‎(1)y=400+60t-120=60()2+40(1≤t≤24),‎ 当t=6时，ymin=40(吨),‎ 故从供水开始到第6小时，蓄水池中的存水量最少，最少存水为40吨.‎ ‎(2)依条件知60()2+40<80,1≤t≤24,‎ 解得0，二次函数f(a)图象开口方向向上,‎ 当a=(a1+a2+…+an)时，y有最小值,‎ 所以a=(a1+a2+…+an)即为所求.‎ 点评：此题在高考中是具有导向意义的试题，它以物理知识和简单数学知识为基础，并以物理学科中的统计问题为背景，给出一个新的定义，要求学生读懂题目，抽象其中的数量关系，将文字语言转化为符号语言，即y=(a-a1)2+(a-a2)2+…+(a-an)2,然后运用函数的思想方法去解决问题.解题关键是将函数式化成以a为自变量的二次函数形式，这是函数思想在解决实际问题中的应用.‎ 课堂小结 ‎1.巩固函数模型的应用.‎ ‎2.初步掌握函数拟合思想，并会用函数拟合思想解决实际问题.‎ 作业 课本P107习题3.2B组1、2.‎ 设计感想 本节通过事例引入课题，接着通过事例让学生感受什么是函数拟合；课本的例3是函数模型的应用，例4是函数拟合的应用，这都是本节的重点.因此本节选用了多个地市的模拟试题进行强化训练，其中开放性函数拟合问题更值得关注.本节素材鲜活丰富，结构合理有序，难度适中贴近高考.‎ 习题详解 ‎(课本第98页练习)‎ ‎1.y2.‎ ‎2.设第1轮病毒发作时有a1=10台被感染,第2轮,第3轮,…,依次有a2台,a3台,…被感染,依题意有a5=10×204=160.‎ 答:在第5轮病毒发作时会有160万台被感染.‎ ‎(课本第101页练习)‎ 三个函数图象如下:‎ 图3-2-2-9‎ 由图象可以看到,函数(1)以“爆炸”式的速度增长;函数(2)增长缓慢,并渐渐趋于稳定;函数(3)以稳定的速度增加.‎ ‎(课本第104页练习)‎ ‎1.(1)已知人口模型为y=y0ert,‎ 其中y0表示t=0时的人口数,r表示人口的年增长率.‎ 若按1650年世界人口5亿,年增长率为0.3%估计,有y=5e0.003t.‎ 当y=10时,解得t≈231.‎ 所以,1881年世界人口数约为1650年的2倍.‎ 同理,可知2003年世界人口数约为1970年的2倍.‎ ‎(2)由此看出,此模型不太适宜估计跨度时间非常大的人口增长情况.‎ ‎2.由题意有75t-4.9t2=100,‎ 解得t=,‎ 即t1≈1.480,t2≈13.827.‎ 所以,子弹保持在100 m以上的时间t=t2-t1≈12.35,在此过程中,子弹最大速率 v1=v0-9.8t=75-9.8×1.480=60.498 m/s.‎ 答:子弹保持在100米以上高度的时间是12.35秒,在此过程中,子弹速率的范围是v∈(0,60.498).‎ ‎(课本第106页练习)‎ ‎1.(1)由题意可得y1=150+0.25x,‎ y2=+0.25,‎ y3=0.35x,‎ y4=0.35x-(150+0.25x)=0.1x-150.‎ ‎(2)画出y4=0.1x-150的图象如下.‎ 图3-2-2-10‎ 由图象可知,当x<1500件时,该公司亏损;‎ 当x=1500件时,公司不赔不赚;‎ 当x>1500件时,公司赢利.‎ ‎2.(1)列表.‎ ‎(2)画散点图.‎ 图3-2-2-11‎ ‎3.确定函数模型.‎ 甲:y1=-x2+12x+41,‎ 乙:y2=-52.07×0.778x+92.5.‎ ‎(4)做出函数图象进行比较.‎ 图3-2-2-12‎ 图3-2-2-13‎ 图3-2-2-14‎ 计算x=6时,y1=77,y2=80.9.‎ 可见,乙选择的模型较好.‎ ‎(课本第107页习题3.2)‎ A组 ‎1.(1)列表.‎ ‎(2)描点.‎ 图3-2-2-15‎ ‎(3)根据点的分布特征,可以考虑以d=kf+b作为刻画长度与拉力的函数模型,取两组数据(1,14.2)、(4,57.5),有 解得所以d=14.4f-0.2.‎ 将已知数据带入上述解析式或作出函数图象,可以发现,‎ 这个函数模型与已知数据拟合程度较好,说明它能较好地反映长度与拉力的关系.‎ 图3-2-2-16‎ ‎2.由=(60)2a,得a=.由=x2,得x=3010.‎ 因为3010<100,所以这辆车没有超速.‎ ‎3.(1)x=(2)v=‎ 图略.‎ ‎4.设水池总造价为y元,水池长度为x m,则y=(12x+)95+×135,‎ 画出函数y1=(12x+)95+×135和函数y2=7的图象.‎ 图3-2-2-17‎ 由图可知,若y1≤7,则x应介于［x1,x2］之间,x1,x2即为方程(12x+)95+×135=70 000的两个根.‎ 解得x1≈6.4,x2≈31.3.‎ 答:水池的长与宽应该控制在［6.4,31.3］之间.‎ ‎5.将x=0,y=1.01×105和x=2400,y=0.90×105分别代入y=cekx,得到 解得c=所以y=1.01×105ex.‎ 当x=5596m时,y=0.772×105(Pa)<0.775×105(Pa).‎ 答:这位游客的决定是冒险的决定.‎ ‎6.由500≤2500()t<1500,解得2.3

查看更多