- 2021-07-01 发布 |
- 37.5 KB |
- 17页

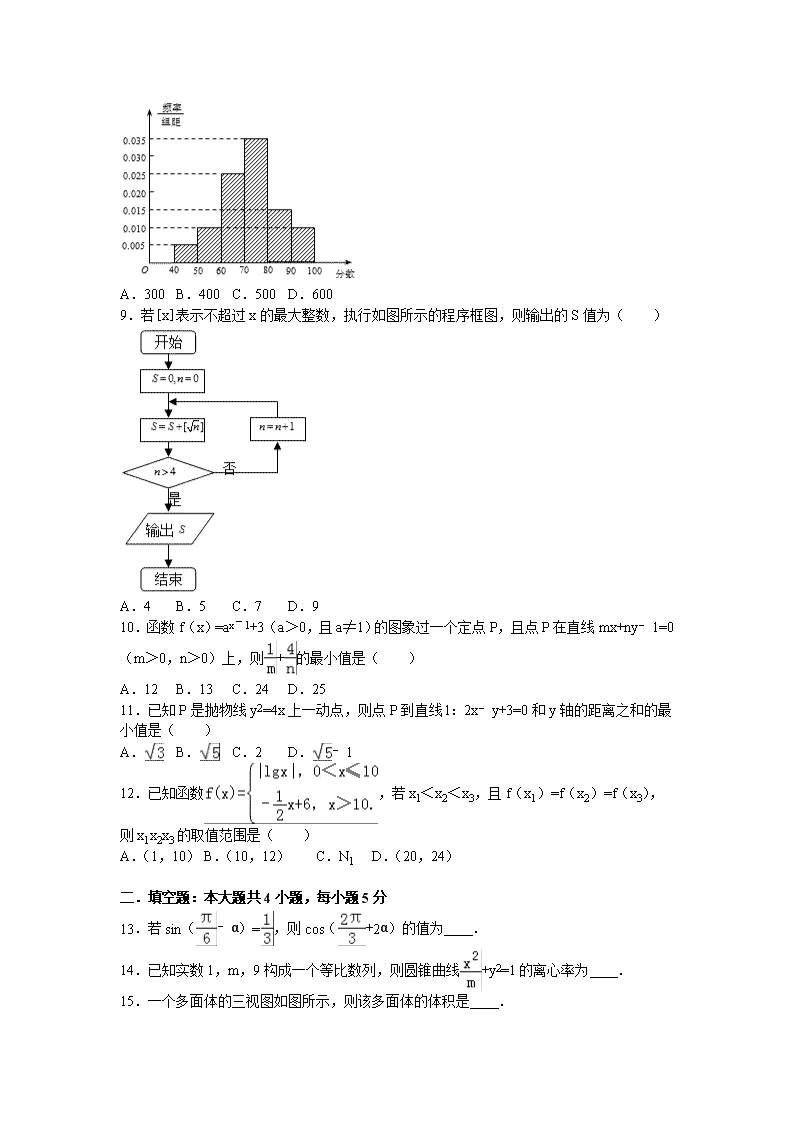

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学卷·2018届辽宁省大连市瓦房店高中高二上学期期中数学试卷(文科) (解析版)
2016-2017学年辽宁省大连市瓦房店高中高二(上)期中数学试卷(文科) 一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3,5},则(∁UA)∪B=( ) A.{3,5} B.{3,4,5} C.{2,3,4,5} D.{1,2,3,4} 2.已知向量=(﹣3,4),=(1,m),若⊥(﹣),m=( ) A. B.7 C.﹣7 D.﹣ 3.某高级中学有高一、二、三三个年级的学生共1600名,其中高三学生400名,如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本,则应从高三年级学生中抽取的人数是( ) A.40 B.30 C.20 D.10 4.北宋 欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其扣,徐以杓酌油沥之,自钱孔入,而钱不湿.因曰:‘我亦无他,唯手熟尔.’”可见技能都能透过反复苦练而达至熟能生巧之境的.若铜钱是半径为1cm的圆,中间有边长为0.5cm的正方形孔,你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( ) A. B. C. D. 5.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( ) A. B. C.2 D. 6.某公司为确定明年投入某产品的广告支出,对近5年的广告支出m与销售额y(单位:百万元)进行了初步统计,得到下列表格中的数据: y 30 40 p 50 70 m 2 4 5 6 8 经测算,年广告支出m与年销售额y满足线性回归方程=6.5m+17.5,则p的值为( ) A.45 B.50 C.55 D.60 7.下列结论正确的是( ) A.“x≠1”是“x2≠1”的充分不必要条件 B.若“p∧q”与“¬p∨q”都是假命题,则p真q假 C.命题“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x<0” D.命题“能被2整除的数是偶数”的逆否命题是“不能被2整除的数不是偶数” 8.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是( ) A.300 B.400 C.500 D.600 9.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出的S值为( ) A.4 B.5 C.7 D.9 10.函数f(x)=ax﹣1+3(a>0,且a≠1)的图象过一个定点P,且点P在直线mx+ny﹣1=0(m>0,n>0)上,则+的最小值是( ) A.12 B.13 C.24 D.25 11.已知P是抛物线y2=4x上一动点,则点P到直线l:2x﹣y+3=0和y轴的距离之和的最小值是( ) A. B. C.2 D.﹣1 12.已知函数,若x1<x2<x3,且f(x1)=f(x2)=f(x3),则x1x2x3的取值范围是( ) A.(1,10) B.(10,12) C.N1 D.(20,24) 二.填空题:本大题共4小题,每小题5分 13.若sin(﹣α)=,则cos(+2α)的值为 . 14.已知实数1,m,9构成一个等比数列,则圆锥曲线+y2=1的离心率为 . 15.一个多面体的三视图如图所示,则该多面体的体积是 . 16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 元. 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.已知函数f(x)=sin(2x﹣)+2cos2x﹣1. (Ⅰ)求函数f(x)的单调增区间; (Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)=,求△ABC的面积. 18.如图,在四棱锥P﹣ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点. (Ⅰ)求证:DE∥平面PAB; (Ⅱ)求证:平面PCD⊥平面PBC. 19.某家电专卖店试销A,B,C三种新型空调,销售情况记录如下: 第一周 第二周 第三周 第四周 第五周 A型数量(台) 10 10 15 A4 A5 B型数量(台) 10 12 13 B4 B5 C型数量(台) 15 8 12 C4 C5 (1)求A型空调前三周的平均周销售量; (2)为跟踪调查空调的使用情况,根据销售记录,从该家电专卖店前三周售出的所有空调中随机抽取一台,求抽到的空调“是B型空调或是第一周售出空调”的概率; (3)根据C型空调连续3周销售情况,预估C型空调连续5周的平均周销量为10台.当C型空调周销售量的方差最小时,求C4,C5的值. 参考公式: 样本数据x1,x2,…,xn的方差是:,其中为样本平均数. 20.已知数列{an}的前n项和Sn=n2﹣2n. (1)求数列{an的通项公式an; (2)令bn=,求数列{bn}的前n项和Tn. 21.垂直于x轴的直线l与椭圆C:相交于M、N两点,A是C的左顶点. (1)求的最小值; (2)设点P是C上异于M、N的任意一点,且直线MP、NP分别与x轴交于R、S两点,O是坐标原点,求△OPR和△OPS的面积之积的最大值. 22.已知函数f(x)=lnx,. (1)若f(x)与g(x)在x=1处相切,试求g(x)的表达式; (2)若在[1,+∞)上是减函数,求实数m的取值范围; (3)证明不等式: . 2016-2017学年辽宁省大连市瓦房店高中高二(上)期中数学试卷(文科) 参考答案与试题解析 一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设全集U={1,2,3,4,5},集合A={1,2},B={2,3,5},则(∁UA)∪B=( ) A.{3,5} B.{3,4,5} C.{2,3,4,5} D.{1,2,3,4} 【考点】交、并、补集的混合运算. 【分析】根据全集U及A,求出A的补集,找出A补集与B的并集即可. 【解答】解:∵全集U={1,2,3,4,5},集合A={1,2},B={2,3,5}, ∴∁UA={3,4,5}, 则(∁UA)∪B={2,3,4,5}. 故选C 2.已知向量=(﹣3,4),=(1,m),若⊥(﹣),m=( ) A. B.7 C.﹣7 D.﹣ 【考点】平面向量数量积的运算. 【分析】令•(﹣)=0列方程解出m. 【解答】解:∵若⊥(﹣),∴若•(﹣)=0,即=. ∴25=﹣3+4m, 解得m=7. 故选:B. 3.某高级中学有高一、二、三三个年级的学生共1600名,其中高三学生400名,如果通过分层抽样的方法从全体高中学生中抽取一个容量为80人的样本,则应从高三年级学生中抽取的人数是( ) A.40 B.30 C.20 D.10 【考点】分层抽样方法. 【分析】设应当从高三年级的学生中抽取的人数是x,则由分层抽样的定义可得,由此求出x的值. 【解答】解:设应当从高三年级的学生中抽取的人数是x,则由分层抽样的定义可得,解得x=20, 故选:C. 4.北宋 欧阳修在《卖油翁》中写道:“(翁)乃取一葫芦置于地,以钱覆其扣,徐以杓酌油沥之,自钱孔入,而钱不湿.因曰:‘我亦无他,唯手熟尔.’”可见技能都能透过反复苦练而达至熟能生巧之境的.若铜钱是半径为1cm的圆,中间有边长为0.5cm的正方形孔,你随机向铜钱上滴一滴油,则油(油滴的大小忽略不计)正好落入孔中的概率为( ) A. B. C. D. 【考点】几何概型. 【分析】分别计算圆和正方形的面积,由几何概型概率公式可得. 【解答】解:由题意可得半径为1cm的圆的面积为π×12=π, 而边长为0.5cm的正方形面积为0.5×0.5=0.25, 故所求概率P==, 故选:B. 5.直线x﹣y+3=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( ) A. B. C.2 D. 【考点】直线和圆的方程的应用. 【分析】先根据点到直线的距离公式求出圆心到弦的距离即弦心距OD,然后根据垂径定理得到垂足为弦长的中点D,根据勾股定理求出弦长的一半BD,乘以2即可求出弦长AB. 【解答】解:连接OB,过O作OD⊥AB,根据垂径定理得:D为AB的中点, 根据(x+2)2+(y﹣2)2=2得到圆心坐标为(﹣2,2),半径为. 圆心O到直线AB的距离OD==,而半径OB=, 则在直角三角形OBD中根据勾股定理得BD==,所以AB=2BD= 故选D. 6.某公司为确定明年投入某产品的广告支出,对近5年的广告支出m与销售额y(单位:百万元)进行了初步统计,得到下列表格中的数据: y 30 40 p 50 70 m 2 4 5 6 8 经测算,年广告支出m与年销售额y满足线性回归方程=6.5m+17.5,则p的值为( ) A.45 B.50 C.55 D.60 【考点】线性回归方程. 【分析】求出,代入回归方程计算,从而得出p的值. 【解答】解: ==5, ∴=6.5×5+17.5=50, ∴=50,解得p=60. 故选:D. 7.下列结论正确的是( ) A.“x≠1”是“x2≠1”的充分不必要条件 B.若“p∧q”与“¬p∨q”都是假命题,则p真q假 C.命题“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x<0” D.命题“能被2整除的数是偶数”的逆否命题是“不能被2整除的数不是偶数” 【考点】命题的真假判断与应用. 【分析】A,x=﹣1时,x2=1; B,¬p∨q是假命题时,则p真q假,则 p∧q 是假命题; C,命题“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x≤0; D,命题“能被2整除的数是偶数”的逆否命题是“若一个数不是偶数 则不能被2整除; 【解答】解:对于A,x=﹣1时,x2=1也成立,故错; 对于 B,¬p∨q是假命题时,则p真q假,则 p∧q 是一定是假命题,故正确; 对于C,命题“∃x∈R,x2﹣x>0”的否定是“∀x∈R,x2﹣x≤0,故错; D,命题“能被2整除的数是偶数”的逆否命题是“若一个数不是偶数 则不能被2整除,故错; 故选:B. 8.某大学对1000名学生的自主招生水平测试成绩进行统计,得到样本频率分布直方图(如图),则这1000名学生在该次自主招生水平测试中成绩不低于70分的学生数是( ) A.300 B.400 C.500 D.600 【考点】频率分布直方图. 【分析】根据频率分布直方图,算出成绩不低于70分的3个组的面积之和为0.6,从而得到成绩不低于70分的学生的频率为0.6,由此即可得到这1000名学生在该次自主招生水平测试中不低于70分的学生数. 【解答】解:根据频率分布直方图,可得 成绩在70﹣80的小组的小矩形面积为S1=10×0.035=0.35;在80﹣90的小组的小矩形面积为S2=10×0.015=0.15 在90﹣100的小组的小矩形面积为S3=10×0.010=0.10 ∴成绩不低于70分的学生所在组的面积之和为S=S1+S2+S3=0.6 即成绩不低于70分的学生的频率为0.6,由此可得 这1000名学生在该次自主招生水平测试中不低于70分的学生数是1000×0.6=600 故选:D. 9.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出的S值为( ) A.4 B.5 C.7 D.9 【考点】程序框图. 【分析】根据题意,模拟程序框图的运行过程,求出该程序运行后输出的S的值. 【解答】解:模拟程序框图的运行过程,如下; S=0,n=0,S=0+[]=0,0>4,否; n=1,S=0+[]=1,1>4,否; n=2,S=1+[]=2,2>4,否; n=3,S=2+[]=3,3>4,否; n=4,S=3+[]=5,4>4,否; n=5,S=5+[]=7,5>4,是; 输出S=7. 故选:C. 10.函数f(x)=ax﹣1+3(a>0,且a≠1)的图象过一个定点P,且点P在直线mx+ny﹣1=0(m>0,n>0)上,则+的最小值是( ) A.12 B.13 C.24 D.25 【考点】基本不等式. 【分析】函数f(x)=ax﹣1+3(a>0,且a≠1)的图象过一个定点P(1,4),可得m+4n=1.再利用“乘1法”与基本不等式的性质即可得出. 【解答】解:函数f(x)=ax﹣1+3(a>0,且a≠1)的图象过一个定点P(1,4), ∵点P在直线mx+ny﹣1=0(m>0,n>0)上, ∴m+4n=1. 则+=(m+4n)=17+≥17+4×2=25,当且仅当m=n=时取等号. 故选:D. 11.已知P是抛物线y2=4x上一动点,则点P到直线l:2x﹣y+3=0和y轴的距离之和的最小值是( ) A. B. C.2 D.﹣1 【考点】抛物线的简单性质. 【分析】作图,化点P到直线l:2x﹣y+3=0和y轴的距离之和为PF+PA﹣1,从而求最小值. 【解答】解:由题意作图如右图, 点P到直线l:2x﹣y+3=0为PA; 点P到y轴的距离为PB﹣1; 而由抛物线的定义知, PB=PF; 故点P到直线l:2x﹣y+3=0和y轴的距离之和为PF+PA﹣1; 而点F(1,0)到直线l:2x﹣y+3=0的距离为 =; 故点P到直线l:2x﹣y+3=0和y轴的距离之和的最小值为﹣1; 故选D. 12.已知函数,若x1<x2<x3,且f(x1)=f(x2)=f(x3),则x1x2x3的取值范围是( ) A.(1,10) B.(10,12) C.N1 D.(20,24) 【考点】函数的值. 【分析】作函数的图象,从而结合图象可知lgx1=lgx2=﹣x3+6,从而求得. 【解答】解:作函数的图象如下, , ∵x1<x2<x3,f(x1)=f(x2)=f(x3), ∴﹣lgx1=lgx2=﹣x3+6, ∴x1x2=1,10<x3<12, ∴10<x1x2x3<12. 故选:B. 二.填空题:本大题共4小题,每小题5分 13.若sin(﹣α)=,则cos(+2α)的值为 . 【考点】二倍角的余弦;角的变换、收缩变换. 【分析】利用二倍角的余弦公式把要求的式子化为2﹣1,再利用诱导公式化为2﹣1,将条件代入运算求得结果. 【解答】解:∵=cos2(+α)=2﹣1=2﹣1 =2×﹣1=, 故答案为:. 14.已知实数1,m,9构成一个等比数列,则圆锥曲线+y2=1的离心率为 或2 . 【考点】椭圆的简单性质;双曲线的简单性质. 【分析】由1,m,9构成一个等比数列,得到m=±3.当m=3时,圆锥曲线是椭圆;当m=﹣3时,圆锥曲线是双曲线,由此入手能求出离心率. 【解答】解:∵1,m,9构成一个等比数列, ∴m=±3. 当m=3时,圆锥曲线+y2=1是椭圆,它的离心率是=; 当m=﹣3时,圆锥曲线+y2=1是双曲线,它的离心率是2. 故答案为:或2. 15.一个多面体的三视图如图所示,则该多面体的体积是 . 【考点】由三视图求面积、体积. 【分析】判断几何体的形状,结合三视图的数据,求出几何体的体积. 【解答】解:由三视图可知,该多面体是由正方体截去两个正三棱锥所成的几何体,如图, 正方体棱长为2,正三棱锥侧棱互相垂直,侧棱长为1, V=V正方体﹣2V三棱锥=2×2×2=. 故答案我: 16.某高科技企业生产产品A和产品B需要甲、乙两种新型材料.生产一件产品A需要甲材料1.5kg,乙材料1kg,用5个工时;生产一件产品B需要甲材料0.5kg,乙材料0.3kg,用3个工时,生产一件产品A的利润为2100元,生产一件产品B的利润为900元.该企业现有甲材料150kg,乙材料90kg,则在不超过600个工时的条件下,生产产品A、产品B的利润之和的最大值为 216000 元. 【考点】简单线性规划的应用. 【分析】设A、B两种产品分别是x件和y件,根据题干的等量关系建立不等式组以及目标函数,利用线性规划作出可行域,通过目标函数的几何意义,求出其最大值即可; 【解答】解:(1)设A、B两种产品分别是x件和y件,获利为z元. 由题意,得,z=2100x+900y. 不等式组表示的可行域如图:由题意可得,解得:,A(60,100), 目标函数z=2100x+900y.经过A时,直线的截距最大,目标函数取得最大值:2100×60+900×100=216000元. 故答案为:216000. 三.解答题:解答应写出文字说明,证明过程或演算步骤. 17.已知函数f(x)=sin(2x﹣)+2cos2x﹣1. (Ⅰ)求函数f(x)的单调增区间; (Ⅱ)在△ABC中,a、b、c分别是角A、B、C的对边,且a=1,b+c=2,f(A)=,求△ABC的面积. 【考点】正弦函数的单调性;余弦定理. 【分析】(Ⅰ)函数f(x)展开后,利用两角和的公式化简为一个角的一个三角函数的形式,结合正弦函数的单调增区间求函数f(x)的单调增区间. (Ⅱ)利用f(A)=,求出A的大小,利用余弦定理求出bc的值,然后求出△ABC的面积. 【解答】解:(Ⅰ)因为= = = 所以函数f(x)的单调递增区间是〔〕(k∈Z) (Ⅱ)因为f(A)=,所以 又0<A<π所以 从而故A= 在△ABC中,∵a=1,b+c=2,A= ∴1=b2+c2﹣2bccosA,即1=4﹣3bc. 故bc=1 从而S△ABC= 18.如图,在四棱锥P﹣ABCD中,侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°,AD∥BC,PA=AB=BC=2AD,E是PC的中点. (Ⅰ)求证:DE∥平面PAB; (Ⅱ)求证:平面PCD⊥平面PBC. 【考点】平面与平面垂直的判定;直线与平面平行的判定. 【分析】(Ⅰ)取PB中点F,连接EF,AF,推导出四边形DEFA是平行四边形,由此能证明DE∥平面PAB. (Ⅱ)由已知推导出AF⊥BC,AF⊥PB,从而AF⊥平面PBC,再由DE∥AF,能证明平面PCD⊥平面PBC. 【解答】证明:(Ⅰ)取PB中点F,连接EF,AF, 由已知EF∥BC∥AD,且2EF=2AD=BC, 所以,四边形DEFA是平行四边形, 于是DE∥AF,AF⊂平面PAB,DE⊄平面PAB, 因此DE∥平面PAB. … (Ⅱ)侧面PAB⊥底面ABCD,且∠PAB=∠ABC=90°, 所以BC⊥平面PAB,AF⊂平面PAB,所以AF⊥BC, 又因为PA=AB,F是PB中点,于是AF⊥PB, PB∩BC=B,所以AF⊥平面PBC, 由(Ⅰ)知DE∥AF,故DE⊥平面PBC, 而DE⊂平面PCD, 因此平面PCD⊥平面PBC. … 19.某家电专卖店试销A,B,C三种新型空调,销售情况记录如下: 第一周 第二周 第三周 第四周 第五周 A型数量(台) 10 10 15 A4 A5 B型数量(台) 10 12 13 B4 B5 C型数量(台) 15 8 12 C4 C5 (1)求A型空调前三周的平均周销售量; (2)为跟踪调查空调的使用情况,根据销售记录,从该家电专卖店前三周售出的所有空调中随机抽取一台,求抽到的空调“是B型空调或是第一周售出空调”的概率; (3)根据C型空调连续3周销售情况,预估C型空调连续5周的平均周销量为10台.当C型空调周销售量的方差最小时,求C4,C5的值. 参考公式: 样本数据x1,x2,…,xn的方差是:,其中为样本平均数. 【考点】极差、方差与标准差. 【分析】(1)根据数表中的数值计算平均数即可; (2)方法1:根据概率的定义进行计算即可; 方法2:利用对立事件的概率公式进行计算也可; (3)根据方差的定义可得S2的解析式,再根据二次函数性质求出 c4=7或c4=8时,S2取得最小值,从而求出c5的值. 【解答】解:(1)A型空调前三周的平均销售量为 (台);… (2)方法1:从前三周售出的所有空调中随机抽取一台,有105种可能, 其中“是B型或是第一周售出空调”有35+35﹣10=60;… 因此抽到的空调“是B型或是第一周售出空调”的概率是;… 方法2:设抽到的空调“不是B型也不是第一周售出空调”的事件是M, 抽到的空调“是B型或是第一周售出空调”的事件是N, 则, ;… 故抽到的空调“是B型或是第一周售出空调”的概率是;… (3)因为C型空调平均周销售量为10台, 所以c4+c5=10×5﹣15﹣8﹣12=15;… 又, 化简得.… 因为c4∈N, 所以c4=7或c4=8时,S2取得最小值, 此时C5=8或C5=7… 20.已知数列{an}的前n项和Sn=n2﹣2n. (1)求数列{an的通项公式an; (2)令bn=,求数列{bn}的前n项和Tn. 【考点】数列的求和. 【分析】(1)由题意得,当n=1时a1=s1=﹣1,当n≥2时an=sn﹣sn﹣1=2n﹣3,再验证n=1时是否成立即可; (2)由(1)和题意求出bn,利用错位相减法求出数列{bn}的前n项和Tn. 【解答】解:(1)当n=1时,a1=s1=1﹣2=﹣1… 当n≥2时,an=sn﹣sn﹣1=n2﹣2n﹣[(n﹣1)2﹣2(n﹣1)]=2n﹣3… 又a1=﹣1=2﹣3,也符合上式,… 因此,an=2n﹣3… (2)由(1)得,bn==, 所以Tn= ①, Tn= ②, ①﹣②得, Tn=+2()﹣ =+2×﹣= 所以Tn=. 21.垂直于x轴的直线l与椭圆C:相交于M、N两点,A是C的左顶点. (1)求的最小值; (2)设点P是C上异于M、N的任意一点,且直线MP、NP分别与x轴交于R、S两点,O是坐标原点,求△OPR和△OPS的面积之积的最大值. 【考点】椭圆的简单性质. 【分析】(1)点M、N关于x轴对称,设M(x1,y1)(y1>0),则N(x1,﹣y1),利用数量积运算性质、二次函数的单调性即可得出. (2)利用点与椭圆的位置关系、三角形面积计算公式即可得出. 【解答】解:(1)点M、N关于x轴对称,设M(x1,y1)(y1>0),则N(x1,﹣y1), ∵A(﹣2,0),∴,, ∵点M在C上,∴, ∴, ∵x1∈(﹣2,2),∴时,取最小值. (2)设P(x0,y0),则直线MP的方程为:, 令y=0,得,同理, ∵点M、P在C上,∴,, ∴, , ∵y0∈[﹣1,1],∴y0=±1时,S△OPS•S△OPR取最大值1. 22.已知函数f(x)=lnx,. (1)若f(x)与g(x)在x=1处相切,试求g(x)的表达式; (2)若在[1,+∞)上是减函数,求实数m的取值范围; (3)证明不等式: . 【考点】利用导数研究函数的单调性;利用导数研究曲线上某点切线方程. 【分析】(1)求导数,利用f(x)与g(x)在x=1处相切,可求g(x)的表达式; (2)在[1,+∞)上是减函数,可得导函数小于等于0,在[1,+∞)上恒成立,分离参数,利用基本不等式,可求实数m的取值范围; (3)当x≥2时,证明,当x=2时,当x=3时,当x=4时,…,当x=n+1时,利用叠加法,即可得到结论. 【解答】解:(1)∵f(x)=lnx,∴,∴,得:a=2. 又∵,∴b=﹣1, ∴g(x)=x﹣1; (2)=在[1,+∞)上是减函数, ∴在[1,+∞)上恒成立. 即x2﹣(2m﹣2)x+1≥0在[1,+∞)上恒成立,由,x∈[1,+∞), ∵, ∴2m﹣2≤2得m≤2; 证明:(3)由(1)可得:当x≥2时:,∴得:, ∴. 当x=2时:, 当x=3时:, 当x=4时:, … 当x=n+1时:,n∈N+,n≥2, 上述不等式相加得: , 即: . 查看更多