专题12-5 压轴题高分策略之计数原理的综合应用-《奇招制胜》2017年高考数学（理）热点 题型全突破

专题12-5 压轴题高分策略之计数原理的综合应用-《奇招制胜》2017年高考数学（理）热点 题型全突破

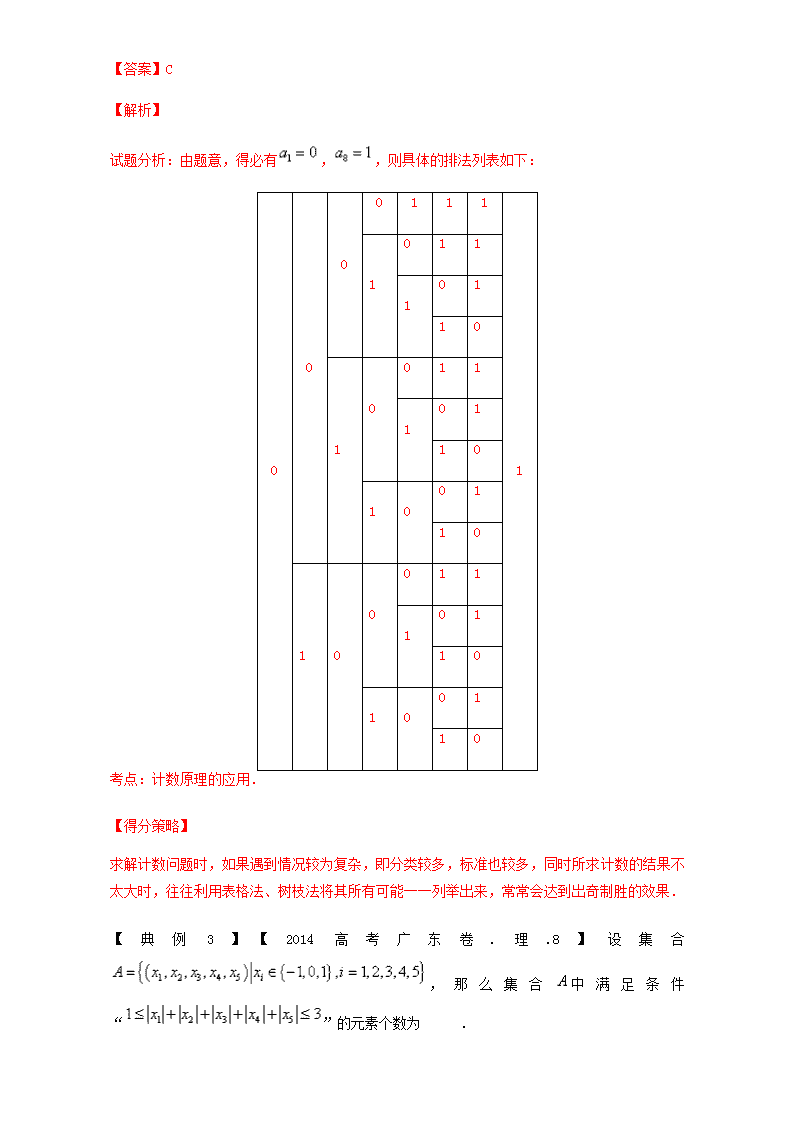
压轴题高分策略之计数原理的综合应用 计数原理与概率交汇主要以压轴题的形式出现，试题还可能涉及到与期望等知识综合一起考查．主要考查分类讨论、归纳思想。图表分析法。 ‎ 一、排列组合和古典概型 ‎【典例1】【2014高考广东卷.理.11】从.........中任取七个不同的数，则这七个数的中位数是的概率为 . ‎ ‎【答案】.‎ 考点：本题考查排列组合与古典概型的概率计算，属于能力题.‎ ‎【得分策略】‎ 本题主要考查的是排列组合和古典概型，属于中等题．解题时要抓住重要字眼“中位数是”，否则很容易出现错误．用排列组合列举基本事件一定要做到不重不漏，防止出现错误．解本题需要掌握的知识点是古典概型概率公式，即．‎ ‎【典例2】【陕西师范大学附属中学2016-2017学年高二第二学期期中数学理】电子钟一天显示的时间从00：00到23：59，每一时刻都由4个数字组成，则一天中任一时刻显示的四个数字之和是23的概率是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】一天显示的时间总共有 种，和为 有 ，总共有种，故所求概率为 ，故选D.‎ ‎【变式训练】‎ ‎1．【2017年天津市河东区高三二模数学（理科）】为丰富少儿文体活动，某学校从篮球，足球，排球，橄榄球中任选2种球给甲班学生使用，剩余的2种球给乙班学生使用，则篮球和足球不在同一班的概率是( )‎ A. B. C. D. ‎ ‎【答案】C ‎2.将5本不同的书全发给4名同学，每名同学至少有一本书的概率是（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】本书全分给名同学共有 种分法，其中每名同学至少有一本书的分法共有 种，所以本书全分给名同学，每名同学至少有一本书的 概率为 ，故选B.‎ 二、计数原理的应用．‎ ‎【典例2】【2016高考新课标3理数】定义“规范01数列”如下：共有项，其中项为0， ‎ 项为1，且对任意，中0的个数不少于1的个数.若，则不同的“规范01数列”‎ 有（ ）‎ ‎（A）18个 （B）16个 （C）14个 （D）12个 ‎【答案】C ‎【解析】‎ 试题分析：由题意，得必有，，则具体的排法列表如下：‎ ‎0‎ ‎0‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ ‎1‎ ‎0‎ ‎0‎ ‎1‎ ‎1‎ ‎0‎ 考点：计数原理的应用．‎ ‎【得分策略】‎ 求解计数问题时，如果遇到情况较为复杂，即分类较多，标准也较多，同时所求计数的结果不太大时，往往利用表格法、树枝法将其所有可能一一列举出来，常常会达到岀奇制胜的效果．‎ ‎【典例3】【2014高考广东卷.理.8】设集合，那么集合中满足条件“”的元素个数为 . ‎ ‎【答案】130‎ 考点：本题考查分类计数原理，属于拔高题 ‎【得分策略】‎ 本题主要考查的是分类计数原理，属于难题．解题时一定要注意选出的元素是否与顺序有关，否则很容易出现错误．利用排列组合计数时，关键是正确进行分类和分步，分类时要做到不重不漏，防止出现错误．‎ ‎【变式训练】‎ ‎1.【北京市西城区2017届高三4月统一测试（一模）数学理】将五个1，五个2，五个3，五个4，五个5共25个数填入一个5行5列的表格内（每格填入一个数），使得同一行中任何两数之差的绝对值不超过2，考查每行中五个数之和，记这五个和的最小值为，则的最大值为（ ）‎ A. B. 9 C. 10 D. 11‎ ‎【答案】C ‎【解析】依据5个1分布的列数的不同情形进行讨论,确定的最大值. (1)若5个1分布在同一列，则；(2)若5个1分布在两列中，则由题意知这两列中出现的最大数至多为3，故,故；(3)若5个1分布在三列中，则由题意知这三列中出现的最大数至多为3，故,故； (4)若5个1分布在至少四列中，则其中某一列至少有一个数大于3，这与已知矛盾.  综上所述， ‎ ‎；  另一方面，如下表的例子说明可以取到10.故的最大值为 ‎1‎ ‎1‎ ‎1‎ ‎4‎ ‎5‎ ‎1‎ ‎1‎ ‎2‎ ‎4‎ ‎5‎ ‎2‎ ‎2‎ ‎2‎ ‎4‎ ‎5‎ ‎3‎ ‎3‎ ‎2‎ ‎4‎ ‎5‎ ‎3‎ ‎3‎ ‎3‎ ‎4‎ ‎5‎ ‎2.【上海市宝山区2017届高三4月期中教学质量监控（二模）】设为的一个排列，则满足对任意正整数，且，都有成立的不同排列的个数为_______．‎ ‎【答案】‎ 三、组合数性质的应用 ‎【典例3】【2016高考江苏卷】‎ ‎（1）求 的值；‎ ‎（2）设m，nN*，n≥m，求证： ‎ ‎（m+1）+（m+2）+（m+3）+…+n+（n+1）=（m+1）.‎ ‎【答案】（1）0（2）详见解析 ‎【解析】‎ 试题分析：（1）根据组合数公式化简求值（2）设置（1）目的指向应用组合数性质解决问题，而组合数性质不仅有课本上的 ，而且可由（1）归纳出的 ；单纯从命题角度看，可视为关于n的等式，可结合数学归纳法求证；从求和角度看，左边式子可看做展开式中含项的系数，再利用错位相减求和得含项的系数 ，从而达到化简求证的目的 ‎（1）‎ ‎（2）当时，结论显然成立，当时 又因为 所以 因此 考点：组合数及其性质 ‎【得分策略】‎ 本题从性质上考查组合数性质，从方法上考查利用数学归纳法解决与自然数有关命题，从思想上考查运用算两次解决二项式有关模型. 组合数性质不仅有课本上介绍的、，更有，现在又有，这些性质不需记忆，但需会推导，更需会应用.‎ ‎【变式训练】‎ ‎【江苏省苏锡常镇四市2017届高三教学情况调研（二）5月】已知，其中， ， ， .‎ ‎（1）试求， ， 的值；‎ ‎（2）试猜测关于的表达式，并证明你的结论.‎ ‎【答案】（1）， （2）‎ ‎【解析】试题分析：（1）根据对应以及组合数公式展开化简得， ， 的值；（2）从阶乘角度猜想关于的表达式，证明时注意利用性质及进行转化：配凑成归纳假设的条件.‎ ‎（2）猜想： .‎ 而 ， ，‎ 所以.‎ 用数学归纳法证明结论成立.‎ ‎①当时， ，所以结论成立.‎ ‎②假设当时， .‎ 当时， ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ （*）‎ ‎ ‎ 由归纳假设知（*）式等于 .‎ 所以当时，结论也成立.‎ 综合①②，成立.‎