2020届二轮复习二次函数与幂函数学案（全国通用）

2020届二轮复习二次函数与幂函数学案（全国通用）

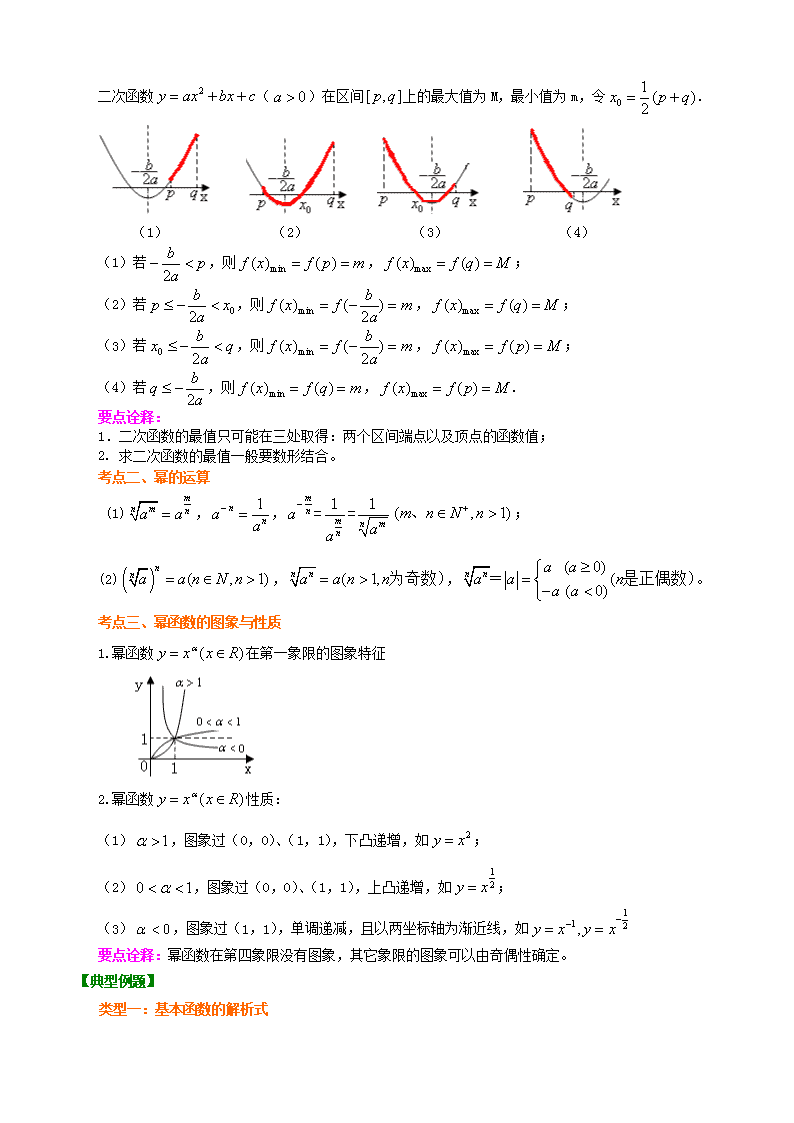
二次函数与幂函数 ‎【考纲要求】‎ ‎1.理解常数函数、一次函数、二次函数、反比例函数的概念、图象与性质。‎ ‎2.幂函数 ‎(1)了解幂函数的概念．‎ ‎(2)结合函数的图象，了解它们的图象的变化情况．‎ ‎【知识网络】‎ 基 本 初 等 函 数 图象与性质 一次函数 二次函数 幂函数 常数函数 ‎【考点梳理】‎ 考点一、初中学过的函数 ‎（一）函数的图象与性质 常 函 数 一次函数 反比例函数 二次函数 表达式 ‎（）‎ ‎（）‎ ‎（）‎ ‎ （）‎ 式子中字母的含义及范围限定 图象、及其与坐 标轴的关系 单 调 性 要点诠释：‎ ‎1.过原点的直线的方程,图象,性质；‎ ‎2.函数的最高次项的系数能否为零。‎ ‎（二）二次函数的最值 ‎1.二次函数有以下三种解析式：‎ 一般式：（），‎ 顶点式：（），其中顶点为，对称轴为直线，‎ 零点式：（），其中是方程的根 ‎2. 二次函数（）在区间上的最值：‎ 二次函数（）在区间上的最大值为M，最小值为m，令.‎ ‎ ‎ ‎ （1） （2） （3） （4）‎ ‎（1）若，则，；‎ ‎（2）若，则，；‎ ‎（3）若，则，；‎ ‎（4）若，则，.‎ 要点诠释：‎ ‎1．二次函数的最值只可能在三处取得：两个区间端点以及顶点的函数值；‎ ‎2. 求二次函数的最值一般要数形结合。‎ 考点二、幂的运算 ‎ (1)，，；‎ ‎(2)，，。‎ 考点三、幂函数的图象与性质 ‎1.幂函数在第一象限的图象特征 ‎2.幂函数性质： ‎ ‎（1），图象过（0，0）、（1，1），下凸递增，如；‎ ‎（2），图象过（0，0）、（1，1），上凸递增，如；‎ ‎（3），图象过（1，1），单调递减，且以两坐标轴为渐近线，如 要点诠释：幂函数在第四象限没有图象，其它象限的图象可以由奇偶性确定。‎ ‎【典型例题】‎ 类型一：基本函数的解析式 例1．已知二次函数满足，且图像在轴上截距为1，在轴截得的线段长为，求的解析式.‎ ‎【解析】‎ ‎【方法一】设（），‎ 则，且对称轴，即，‎ ‎∴，‎ ‎∵ ， ∴‎ ‎∴‎ ‎【方法二】∵，∴二次函数的图象的对称轴为，‎ 可设所求函数为（），‎ ‎∵截轴上的弦长为， ∴的图像过点和，‎ ‎∴，即 （1）‎ 又∵的图像过点， ∴ （2）‎ ‎（1）（2）联立，解得，，‎ ‎∴，即.‎ ‎【方法三】∵的图象对称轴， 又,‎ ‎∴与轴的交点为和，‎ 故可设（），‎ 由可得 . ‎ ‎∴，即.‎ ‎【总结升华】二次函数的形式有以下三种：‎ ‎（1）一般形式：（），‎ ‎（2）顶点式（或称配方式）（），‎ ‎（3）零点式（或称双根式）（），（前提：有根）‎ 对一个具体二次函数，三种形式的系数都具有具体的意义，在分析具体问题时，要充分挖掘题目的隐含条件及充分利用图形的直观性去简化运算，简捷处理问题。‎ 举一反三：‎ ‎【变式】已知二次函数的对称轴为，截轴上的弦长为，且过点 ‎，求函数的解析式 ‎【答案】∵二次函数的对称轴为，可设所求函数为，‎ 又∵截轴上的弦长为，∴过点和，‎ 又过点，‎ ‎∴，解得，‎ ‎∴，即.‎ 类型二：函数的图象和性质 例2. 下图是指数函数（1），（2），（3），（4）的图象，则、、、与1的大小关系是（ ）‎ A. B. C. D.‎ ‎【解析】可先分两类，即（3）（4）的底数一定大于1，（1）（2）的底数小于1，然后再从（3）（4）中比较、的大小，从（1）（2）中比较、的大小.‎ ‎【答案】B ‎【总结升华】可以依据函数系的性质和图象变化解答，但作为选择题更多地利用特殊点解决.‎ 举一反三：‎ ‎【变式】‎ ‎（1）下图的曲线是对数函数图象，已知的取值为10，2，0.6，0.25，则曲线对应的的值依次为 ；‎ ‎（2）如图是幂函数在第一象限内的图象，已知取，则曲线对应的的值依次为 ； ‎ ‎【答案】‎ ‎（1）依据对数函数的图象中的特殊点，如图，令，‎ 由图知点、、、的左右位置关系，有，‎ ‎∴相对应的曲线的值依次为2、10、0.25、0.6.‎ ‎（2）依据幂函数在第一象限内的图象特征，如图，令，‎ 由图知点、、、的上下位置关系，有 ‎，‎ ‎∴相对于曲线的依次为、、、.‎ 类型三：比较大小 例3. 比较 ， ，这三个数的大小关系．‎ ‎【解析】比较式子的结构，依据其异同点选用不同的函数，结合函数的单调性或数形结合比较大小。‎ ‎【方法一】考察函数，由于该函数是单调递减函数，故 ．‎ 考察函数，由于该函数在第一象限是单调递增函数，故 ‎∴ ， ，这三个数的大小关系是： ‎ ‎【方法一】考察函数，由于该函数是单调减函数，故 考察函数与函数，根据指数函数图象的分布规律知，‎ 在第一象限时的图象位于的图象的上方，‎ 从而当自变量都取时，。‎ ‎∴ ， ，这三个数的大小关系是： ‎ ‎【总结升华】大小比较是此处常见的一类考题。通常都是构想函数运用函数性质来解决，通常两个同指的幂式比较就构想幂函数，同底的就构想指数函数，若混合比较即插入对数式或底指皆不同的幂式就用搭桥的办法，常用搭桥的思路有选0或选1或根据具体情况构作。‎ 举一反三：‎ ‎【变式】‎ ‎（1）设，且（，），则与的大小关系是（ ）‎ ‎ A. B. C. D. ‎ ‎(2) 若，则，，从小到大依次为 ；‎ ‎【答案】‎ ‎（1）取，知选。‎ ‎ (2) ；‎ ‎ 【方法一】由得，故.‎ ‎【方法二】令，可得，故.‎ 类型四：最值问题 例4.求函数（)的最值.‎ ‎【解析】令, 则,‎ 开口向上，对称轴 ‎ ∵,∴ , 即 ‎∵，‎ ‎∴时，；时，；时，；‎ ‎∴时，；‎ 时，.‎ ‎【总结升华】‎ ‎1. 基本函数的最值问题一般都利用函数的单调性，并数形结合解决之；‎ ‎2. 形如(,且)的函数，可以转化为二次函数，但应注意的取值范围.‎ 举一反三：‎ ‎【变式】已知，，求的最值。‎ ‎【答案】由已知得，‎ ‎∵，∴即，‎ ‎∵对称轴，‎ ‎∴当时，；当时，；当时，；‎ ‎∴当时，取得最小值；‎ 当时，取得最大值16.‎ 例5. （2017浙江卷）已知函数f（x）=x2+bx，则“b<0”是“f（f（x））的最小值与f（x）的最小值相等”的（ ）‎ A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分也不必要条件 A 由题意知，最小值为.‎ 令，则，‎ 当时，的最小值为，所以“”能推出“的最小值与的最小值相等”；‎ 当时，的最小值为0，的最小值也为0，所以“的最小值与的最小值相等”不能推出“”．‎ ‎【总结升华】二次函数最值问题采用配方法，数形结合。同时解题时一定要注意时，是的充分条件，是的必要条件，否则很容易出现错误．‎