2017届高考文科数学(全国通用)二轮文档讲义:第3编应试技能专训-3压轴题专练
三、压轴题专练
(一)
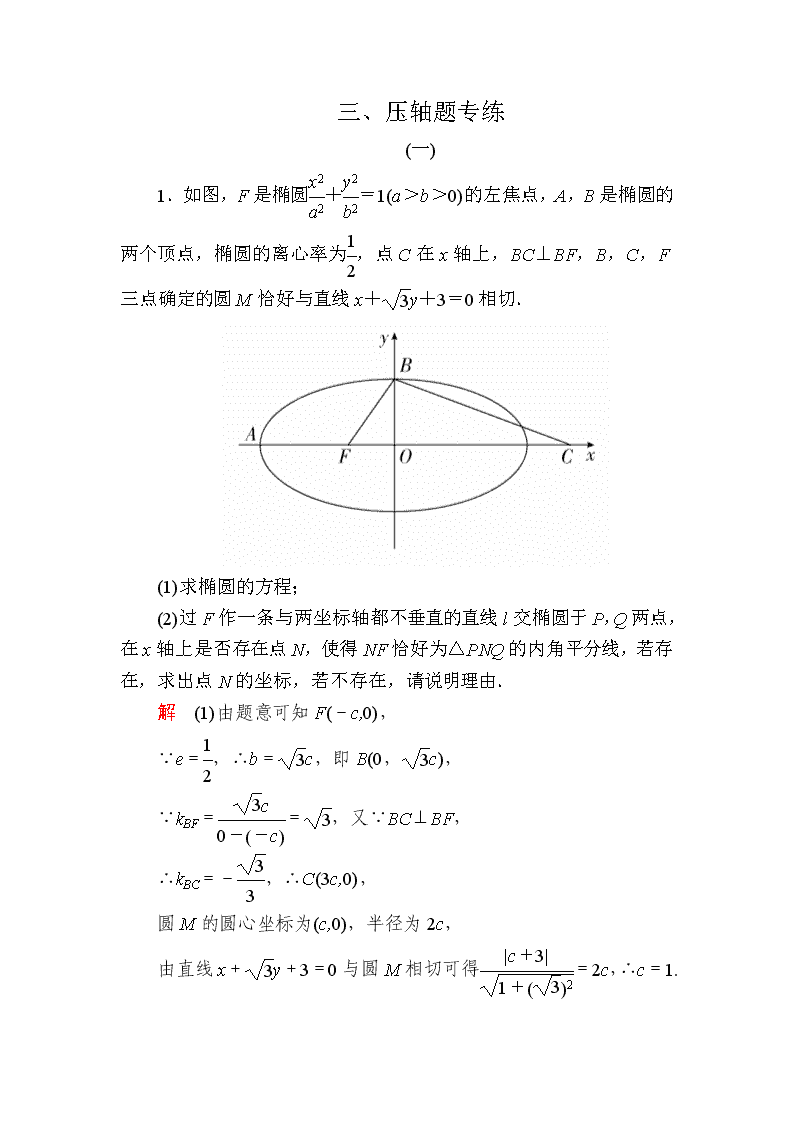
1.如图,F是椭圆+=1(a>b>0)的左焦点,A,B是椭圆的两个顶点,椭圆的离心率为,点C在x轴上,BC⊥BF,B,C,F三点确定的圆M恰好与直线x+y+3=0相切.
(1)求椭圆的方程;
(2)过F作一条与两坐标轴都不垂直的直线l交椭圆于P,Q两点,在x轴上是否存在点N,使得NF恰好为△PNQ的内角平分线,若存在,求出点N的坐标,若不存在,请说明理由.
解 (1)由题意可知F(-c,0),
∵e=,∴b=c,即B(0,c),
∵kBF==,又∵BC⊥BF,
∴kBC=-,∴C(3c,0),
圆M的圆心坐标为(c,0),半径为2c,
由直线x+y+3=0与圆M相切可得=2c,∴c=1.∴椭圆的方程为+=1.
(2)假设存在满足条件的点N(x0,0)
由题意可设直线l的方程为y=k(x+1)(k≠0),
设P(x1,y1),Q(x2,y2),
∵NF为△PNQ的内角平分线,
∴kNP=-kNQ,即=-,
∴=⇒(x1+1)(x2-x0)=-(x2+1)(x1-x0).∴x0=.
又∴3x2+4k2(x+1)2=12.
∴(3+4k2)x2+8k2x+4k2-12=0.
∴x1+x2=-,x1x2=.
∴x0==-4,
∴存在满足条件的点N,点N的坐标为(-4,0).
2.设函数f(x)=x2-mln x,g(x)=x2-(m+1)x.
(1)求函数f(x)的单调区间;
(2)当m≥0时,讨论函数f(x)与g(x)图象的交点个数.
解 (1)函数f(x)的定义域为(0,+∞),f′(x)=,
当m≤0时,f′(x)>0,所以函数f(x)的单调递增区间是(0,+∞),无单调递减区间.
当m>0时,f′(x)=,
当0
时,f′(x)>0,函数f(x)单调递增.
综上:当m≤0时,函数f(x)的单调递增区间是(0,+∞
),无单调递减区间;当m>0时,函数f(x)的单调递增区间是(,+∞),单调递减区间是(0,).
(2)令F(x)=f(x)-g(x)=-x2+(m+1)x-mln x,x>0,问题等价于求函数F(x)的零点个数,
当m=0时,F(x)=-x2+x,x>0,有唯一零点;
当m≠0时,F′(x)=-,
当m=1时,F′(x)≤0,函数F(x)为减函数,注意到F(1)=>0,F(4)=-ln 4<0,所以F(x)有唯一零点.
当m>1时,0m时,F′(x)<0;10,所以函数F(x)在(0,1)和(m,+∞)上单调递减,在(1,m)上单调递增,注意到F(1)=m+>0,
F(2m+2)=-mln (2m+2)<0,所以F(x)有唯一零点.
当01时,F′(x)<0;m0,
所以函数F(x)在(0,m)和(1,+∞)上单调递减,在(m,1)上单调递增,易得ln m<0,
所以F(m)=(m+2-2ln m)>0,而F(2m+2)=-mln (2m+2)<0,所以F(x)有唯一零点.
综上,函数F(x)有唯一零点,即两函数图象有一个交点.
3.选做题
(1)选修4-4:坐标系与参数方程
在直角坐标系xOy中,直线l的参数方程为(t为参数).在以原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ= .
①直接写出直线l的普通方程、曲线C的直角坐标方程;
②设曲线C上的点到直线l的距离为d,求d的取值范围.
(2)选修4-5:不等式选讲
设函数f(x)=|2x-a|+2a.
①若不等式f(x)≤6的解集为{x|-6≤x≤4},求实数a的值.
②在①的条件下,若不等式f(x)≤(k2-1)x-5的解集非空,求实数k的取值范围.
解 (1)①直线l的普通方程为x-y+3=0.
曲线C的直角坐标方程为3x2+y2=3.
②∵曲线C的直角坐标方程为3x2+y2=3,
即x2+=1,
∴曲线C上的点的坐标可表示为(cosα,sinα).
∵2sin+3≥1>0,
∴d==
=.
∴d的最小值为=,d的最大值为=.
∴≤d≤,即d的取值范围为.
(2)①∵|2x-a|+2a≤6,∴|2x-a|≤6-2a,
∴2a-6≤2x-a≤6-2a,
∴a-3≤x≤3-,
∵不等式f(x)≤6的解集为{x|-6≤x≤4},
∴解得a=-2.
②由①得f(x)=|2x+2|-4.
∴|2x+2|-4≤(k2-1)x-5,
化简整理得|2x+2|+1≤(k2-1)x,
令g(x)=|2x+2|+1=
y=g(x)的图象如图所示,
要使不等式f(x)≤(k2-1)x-5的解集非空,需k2-1>2或k2-1≤-1,
∴k的取值范围是{k|k>或k<-或k=0}.
(二)
1.[2016·西安质检] 如图所示,已知椭圆C的中心在原点,焦点在x轴上,离心率等于,它的一个顶点恰好在抛物线x2=8y的准线上.
(1)求椭圆C的标准方程;
(2)点P(2,),Q(2,-)在椭圆上,A,B是椭圆上位于直线PQ两侧的动点,当A,B运动时,满足∠APQ=∠BPQ,试问直线AB的斜率是否为定值,请说明理由.
解 (1)设椭圆C的标准方程为+=1(a>b>0).
∵椭圆的一个顶点恰好在抛物线x2=8y的准线y=-2上,
∴-b=-2,解得b=2.
又=,a2=b2+c2,
∴a=4,c=2.
可得椭圆C的标准方程为+=1.
(2)设A(x1,y1),B(x2,y2),
∵∠APQ=∠BPQ,则PA,PB的斜率互为相反数,
可设直线PA的斜率为k,则PB的斜率为-k,
直线PA的方程为:y-=k(x-2),
联立
化为(1+4k2)x2+8k(-2k)x+4(-2k)2-16=0,
∴x1+2=.
同理可得:x2+2==,
∴x1+x2=,x1-x2=,
kAB===.
∴直线AB的斜率为定值.
2.[2016·河南六市一联]已知函数f(x)=aln x-x,g(x)=x2-(1-a)x-(2-a)ln x,其中a∈R.
(1)若g(x)在其定义域内为增函数,求实数a的取值范围;
(2)若函数F(x)=f(x)-g(x)的图象交x轴于A,B两点,AB中点的横坐标为x0,问:函数F(x)的图象在点(x0,F(x0))处的切线能否平行于x轴?
解 (1)g′(x)=2x-(1-a)-
=,
∵g(x)的定义域为{x|x>0},且g(x)在其定义域内为增函数,
∴g′(x)≥0在x>0时恒成立,
则2x2-(1-a)x-(2-a)≥0在x>0时恒成立,
∴a≥5-在x>0时恒成立.
而当x>0时,2(x+1)+>3,
∴a∈[2,+∞).
(2)设F(x)的图象在(x0,F(x0))处的切线平行于x轴,F(x)=2ln x-x2-ax,F′(x)=-2x-a,不妨设A(m,0),B(n,0),00(t∈(0,1)),
∴函数h(t)=ln t-在(0,1)上单调递增,因此h(t)1时,不等式化为x2-x<-x+,所以x∈∅.
综上所述,不等式的解集为.
②证明:由已知任意x1,x2∈[0,1]且x1≠x2,则不妨设x2>x1,
则当x2-x1≤时,|f(x1)-f(x2)|<|x1-x2|≤,
当x2-x1>时,则x1<,且1-x2<,
那么|f(x1)-f(x2)|=|f(x1)-f(0)+f(1)-f(x2)|≤|f(x1)-f(0)|+|f(1)-f(x2)|0).
(1)若a=1,证明:y=f(x)在R上单调递减;
(2)当a>1时,讨论f(x)零点的个数.
解 (1)证明:当x≥1时,f′(x)=-1≤0,f(x)在[1,+∞)上单调递减,f(x)≤f(1)=0;
当x<1时,f′(x)=ex-1-1<0,f(x)在(-∞,1)上单调递减,且此时f(x)>0.
所以y=f(x)在R上单调递减.
(2)若x≥a,则f′(x)=-a≤-a<0(a>1),
所以此时f(x)单调递减,令g(a)=f(a)=ln a-a2+1,
则g′(a)=-2a<0,所以f(a)=g(a)2时,f′(x)>0,f(x)单调递增,
又f(0)=e-1>0,f<0,所以此时f(x)在上有一个零点.
②当a=2时,f(x)=ex-1,此时f(x)在(-∞,2)上没有零点.
③当10,
所以此时f(x)没有零点.
综上,当12时,f(x)有一个零点.
3.选做题
(1)选修4-4:坐标系与参数方程
已知直线l的参数方程为(t为参数),曲线C的极坐标方程为ρ=2sin,直线l与曲线C交于A,B两点,与y轴交于点P.
①求曲线C的直角坐标方程;
②求+的值.
(2)选修4-5:不等式选讲
已知实数m,n满足:关于x的不等式|x2+mx+n|≤|3x2-6x-9|的解集为R.
①求m,n的值;
②若a,b,c∈R+,且a+b+c=m-n,求证:++≤.
解 (1)①利用极坐标公式,把曲线C的极坐标方程
ρ=2sin化为ρ2=2ρsinθ+2ρcosθ,
∴普通方程是x2+y2=2y+2x,
即(x-1)2+(y-1)2=2.
②∵直线l与曲线C交于A,B两点,与y轴交于点P,
把直线l的参数方程代入曲线C的普通方程 (x-1)2+(y-1)2=2中,得t2-t-1=0,
∴
∴+=+
==
==.
(2)①由于解集为R,那么x=3,x=-1都满足不等式,即有
即解得m=-2,n=-3,
经验证当m=-2,n=-3时,不等式的解集是R.
②证明:a+b+c=1,a+b≥2,b+c≥2,c+a≥2,
∴(++)2=a+b+c+2+2+2≤3(a+b+c)=3,
故++≤(当且仅当a=b=c=时取等号).
(四)
1.[2016·石家庄模拟]已知抛物线C:y2=2px(p>0)过点M(m,2),其焦点为F,且|MF|=2.
(1)求抛物线C的方程;
(2)设E为y轴上异于原点的任意一点,过点E作不经过原点的两条直线分别与抛物线C和圆F:(x-1)2+y2=1相切,切点分别为A,B,求证:直线AB过定点.
解 (1)抛物线C的准线方程为x=-,
∴|MF|=m+=2,又4=2pm,即4=2p,
∴p2-4p+4=0,∴p=2,
∴抛物线C的方程为y2=4x.
(2)证明:设点E(0,t)(t≠0),由已知切线不为y轴,设EA:y=kx+t,联立消去y,可得k2x2+(2kt-4)x+t2=0,①
∵直线EA与抛物线C相切,∴Δ=(2kt-4)2-4k2t2=0,即kt=1,代入 ①可得x2-2x+t2=0,∴x=t2,即A(t2,2t).
设切点B(x0,y0),则由几何性质可以判断点O,B关于直线EF:y=-tx+t对称,则
解得
即B.
解法一:直线AB的斜率为kAB=(t≠±1),
直线AB的方程为y=(x-t2)+2t,
整理得y=(x-1),
∴直线AB恒过定点F(1,0),
当t=±1时,A(1,±2),B(1,±1),此时直线AB为x=1,过点F(1,0).
综上,直线AB恒过定点F(1,0).
解法二:直线AF的斜率为kAF=(t≠±1),
直线BF的斜率为kBF==(t≠±1),
∴kAF=kBF,即A,B,F三点共线.
当t=±1时,A(1,±2),B(1,±1),此时A,B,F三点共线.
∴直线AB过定点F(1,0).
2.[2016·贵州测试]设n∈N*,函数f(x)=,函数g(x)=(x>0).
(1)当n=1时,求函数y=f(x)的零点个数;
(2)若函数y=f(x)与函数y=g(x)的图象分别位于直线y=1的两侧,求n的取值集合A;
(3)对于∀n∈A,∀x1,x2∈(0,+∞),求|f(x1)-g(x2)|的最小值.
解 (1)当n=1时,f(x)=,f′(x)=(x>0).
由f′(x)>0得0e.
所以函数f(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
因为f(e)=>0,f=-e<0,所以函数f(x)在(0,e)上存在一个零点;
当x∈(e,+∞)时,f(x)=>0恒成立,
所以函数f(x)在(e,+∞)上不存在零点.
综上得函数f(x)在(0,+∞)上存在唯一一个零点.
(2)对函数f(x)=求导,得f′(x)=(x>0),
由f′(x)>0,得0e.
所以函数f(x)在(0,e)上单调递增,在(e,+∞)上单调递减,
则当x=e时,函数f(x)有最大值f(x)max=f(e)=.
对函数g(x)=(x>0)求导,得g′(x)=(x>0),
由g′(x)>0,得x>n;由g′(x)<0,得00)在直线y=1的上方,
所以g(x)min=g(n)=n>1,解得n0,
所以|f(x1)-g(x2)|的最小值为-=.
3.选做题
(1)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为
(α为参数),以O为极点,x轴的正半轴为极轴,建立极坐标系,曲线C2的极坐标方程为ρ2=4ρsinθ-3.
①求曲线C1的普通方程与曲线C2的直角坐标方程;
②求曲线C1上的点与曲线C2上的点的距离的最小值.
(2)选修4-5:不等式选讲
已知函数f(x)=|x-a|+|x-2a|.
①当a=1时,求不等式f(x)>2的解集;
②若对任意x∈R,不等式f(x)≥a2-3a-3恒成立,求a的取值范围.
解 (1)①x2=2=(sinα+cosα)2=sin2α+1=y,
所以C1的普通方程为y=x2.
将ρ2=x2+y2,ρsinθ=y代入C2的方程得x2+y2=4y-3,
所以C2的直角坐标方程为x2+y2-4y+3=0.
②将x2+y2-4y+3=0变形为x2+(y-2)2=1,它的圆心为C(0,2).
设P(x0,y0)为C1上任意一点,则y0=x,从而|PC|2=(x0-0)2+(y0-2)2=x+(x-2)2=x-3x+4=2+,
所以当x=时,|PC|min=,
故曲线C1上的点与曲线C2上的点的距离的最小值为-1.
(2)①当a=1时,f(x)=|x-1|+|x-2|.
当x≤1时,f(x)=1-x+2-x=3-2x,此时由f(x)>2得x<;
当12无解;
当x>2时,f(x)=x-1+x-2=2x-3,此时由f(x)>2得x>.
综上可得不等式f(x)>2的解集为
∪.
②因为f(x)=|x-a|+|x-2a|≥|(x-a)-(x-2a)|=|a|,故f(x)取得最小值|a|,因此原不等式等价于|a|≥a2-3a-3.
当a≥0时,有a≥a2-3a-3,即a2-4a-3≤0,
解得2-≤a≤2+,此时有0≤a≤2+.
当a<0时,有-a≥a2-3a-3,即a2-2a-3≤0,
解得-1≤a≤3,此时有-1≤a<0.
综上可知a的取值范围是[-1,2+].