2019-2020学年安徽省六安市第一中学高二上学期期末数学（理）试题（解析版）

2019-2020学年安徽省六安市第一中学高二上学期期末数学（理）试题（解析版）

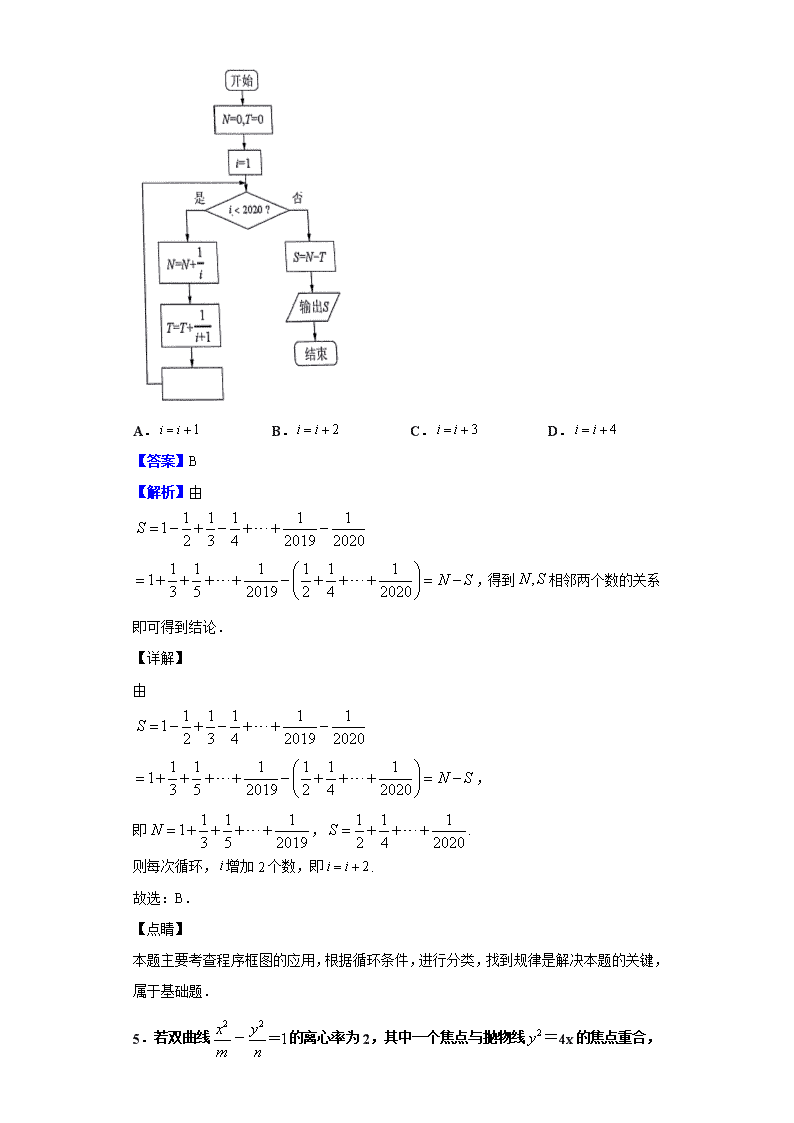
‎2019-2020学年安徽省六安市金安区第一中学高二上学期期末数学（理）试题 一、单选题 ‎1．下列说法错误的是（ ）‎ A．对于命题：，，则：，‎ B．“”是“”的充分不必要条件 C．若命题为假命题，则，都是假命题 D．命题“若，则”的逆否命题为：“若，则”‎ ‎【答案】C ‎【解析】根据非命题的概念可知正确,根据充分不必要条件的概念可知正确,根据真值表可知不正确,根据逆否命题的概念可知正确.‎ ‎【详解】‎ 对于,对于命题：，，则：，是正确的;‎ 对于, “”是“”的充分不必要条件是正确的;‎ 对于,若命题为假命题，则，至少有一个是假命题,故不正确;‎ 对于,命题“若，则”的逆否命题为：“若，则”是正确的.‎ 故选:C ‎【点睛】‎ 本题考查了判断命题的真假,考查了非命题,考查了充分不必要条件,考查了真值表,考查了否命题,属于基础题.‎ ‎2．某中学奥数培训班共有14人，分为两个小组，在一次阶段测试中两个小组成绩的茎叶图如图所示，其中甲组学生成绩的平均数是88，乙组学生成绩的中位数是89，则的值是（ ）．‎ A．5 B．6 C．7 D．8‎ ‎【答案】B ‎【解析】试题分析：甲组学生成绩的平均数是，乙组学生成绩的中位数是89，所以，选B.‎ ‎【考点】平均数，中位数 ‎3．用种不同颜色给甲、乙两个小球随机涂色，每个小球只涂一种颜色，则两个小球颜色不同的概率为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】两个小球颜色不同的对立事件为两个小球颜色相同，先计算得两个小球颜色相同的概率，用减去这个概率，得到两个小球颜色不同的概率.‎ ‎【详解】‎ 基本事件的总数为种，两个小球颜色相同的事件有种，故两个小球颜色相同的概率为，故两个小球颜色不同的概率为.故选A.‎ ‎【点睛】‎ 本小题主要考查古典概型，考查利用对立事件来计算概率.解题过程中如果直接求事件的概率较为复杂时，可以转化为先求该事件的对立事件的概率，然后利用对立事件概率的计算公式，来计算得到事件的概率.在计算基本事件的总数时，要注意颜色能否重复.属于基础题.‎ ‎4．为了计算，设计如图所示的程序框图，则在空白框中应填入（　　）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】由，得到相邻两个数的关系即可得到结论．‎ ‎【详解】‎ 由，‎ 即，.‎ 则每次循环，增加2个数，即.‎ 故选：B．‎ ‎【点睛】‎ 本题主要考查程序框图的应用，根据循环条件，进行分类，找到规律是解决本题的关键，属于基础题．‎ ‎5．若双曲线的离心率为2，其中一个焦点与抛物线＝4x的焦点重合，则mn的值为 A． B． C． D．‎ ‎【答案】A ‎【解析】由题意得解得 ‎6．将一枚质地均匀的骰子先后抛掷两次,若第一次朝上一面的点数为a,第二次朝上一面的点数为b,则函数y=ax2-2bx+1在上为减函数的概率是 (　　)‎ A． B．‎ C． D．‎ ‎【答案】D ‎【解析】函数y=ax2-2bx+1在上为减函数时,满足条件 ‎∵第一次朝上一面的点数为a,第二次朝上一面的点数为b,‎ ‎∴a取1,2时,b可取1,2,3,4,5,6;a取3,4时,b可取2,3,4,5,6;a取5,6时,b可取3,4,5,6,共30种.‎ ‎∵将一枚质地均匀的骰子先后抛掷两次,共有36种等可能发生的结果,‎ ‎∴所求概率为.故选D.‎ ‎7．设，则的最大值为（ ）‎ A． B． C．不存在 D．‎ ‎【答案】D ‎【解析】化简得到，再利用均值不等式计算得到答案.‎ ‎【详解】‎ 当即时等号成立 故选：‎ ‎【点睛】‎ 本题考查了利用均值不等式求函数最值，意在考查学生对于均值不等式的灵活运用.‎ ‎8．已知，则的最大值是（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】设，则，利用三角函数有界性得到最值.‎ ‎【详解】‎ ‎，则设 ，则 当，即时有最大值为 ‎ 故选：‎ ‎【点睛】‎ 本题考查了求最大值，利用参数方程是解题的关键.‎ ‎9．已知一组数据3，4，5，a，b的平均数是4，中位数是m，从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，那么3，4，5，a，b这组数据的方差为（　　）‎ A． B．2 C． D．‎ ‎【答案】D ‎【解析】根据3，4，5，a，b的平均数是4，中位数是m，从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，可知，由方差公式求解即可.‎ ‎【详解】‎ 因为从3，4，5，a，b，m这组数据中任取一数，取到数字4的概率为，所以3，4，5，a，b，m这6个数字中有4个4，‎ 所以，‎ 所以 故选D.‎ ‎【点睛】‎ 本题主要考查了平均数，中位数，概率，方差，属于中档题.‎ ‎10．如图所示，是等边三角形，其内部三个圆的半径相等，且圆心都在的一条中线上.在三角形内任取一点，则该点取自阴影部分的概率为（ ）‎ A． B． C． D．‎ ‎【答案】B ‎【解析】设圆的半径为，利用几何关系得出正三角形的高为，然后利用锐角三角函数计算出，可得出该正三角形的边长，从而可计算出该正三角形的面积，然后将三个圆的面积之和除以正三角形的面积，可计算出所求事件的概率.‎ ‎【详解】‎ 如图所示，取边的中线，则三个圆心都在线段上，‎ 设最上面的圆的圆心为，圆与的切点为，‎ 易知，所以.‎ 设圆的半径，，则，所以.所以 ‎，而阴影部分的面积为，‎ 所以所求的概率.‎ 故选：B.‎ ‎【点睛】‎ 本题考查平面区域型几何概型概率的计算，解题的关键就是计算出相应区域的面积，考查计算能力，属于中等题.‎ ‎11．已知是双曲线的右焦点，动点在双曲线左支上，点为圆上一点，则的最小值为（ ）‎ A． B． C． D．‎ ‎【答案】A ‎【解析】由，的最小值是，转化为求的最小值即为．‎ ‎【详解】‎ 双曲线中，，，，圆半径为，，‎ ‎∴，（当且仅当共线且在间时取等号．‎ ‎∴，当且仅当是线段与双曲线的交点时取等号．‎ ‎∴的最小值是9．‎ 故选：A．‎ ‎【点睛】‎ 本题考查双曲线的标准方程，在涉及到双曲线上的点到焦点的距离时，常常与定义联系，双曲线上点到一个焦点的距离可能转化为到另一个焦点的距离，圆外一点到圆上点的距离的最大值为圆外的点到圆心距离加半径，最小值为圆外的点到圆心距离减半径．‎ ‎12．设为正实数，现有下列命题：‎ ‎①若，则； ②若，则.‎ ‎③若，则；④，则 ‎⑤，则 其中真命题有（ ）个 A． B． C． D．‎ ‎【答案】D ‎【解析】根据均值不等式，柯西不等式依次判断每个选项：取排除②得到答案.‎ ‎【详解】‎ ‎①若，，故，①正确； ‎ ‎②若，取，则，②错误；‎ ‎③若，则，则 当时等号成立，③正确；‎ ‎④，则，④正确；‎ ‎⑤，则 即，当时等号成立，⑤正确；‎ 故选：‎ ‎【点睛】‎ 本题考查了不等式的命题的判断，意在考查学生对于不等式的综合应用.‎ 二、填空题 ‎13．若对任意的，不等式恒成立，则实数的取值范围为________.‎ ‎【答案】‎ ‎【解析】利用绝对值三角不等式求得的最大值为，解不等式，即可得结果 ‎【详解】‎ ‎，‎ 要使恒成立，‎ 则，或，‎ 即或，‎ 实数的取值范围是.故答案为.‎ ‎【点睛】‎ 本题主要考查绝对值三角不等式的应用以及不等式恒成立问题，属于难题．不等式恒成立问题常见方法：① 分离参数恒成立(即可)或恒成立（即可）；② 数形结合( 图象在 上方即可)；③ 讨论最值或恒成立.‎ ‎14．手机运动计步已经成为一种新时尚、某单位统计职工十天行走步数(单位：百步) 得到如下频率分布直方图： ‎ 由频率分布直方图估计该单位职工一天行走步数的中位数为(百步)，则 ‎__________；___________；‎ ‎【答案】 ‎ ‎【解析】计算得到，再根据中位数得到，计算得到，，计算，得到答案.‎ ‎【详解】‎ ‎；；；‎ 中位数为，则，故，则 ‎ ‎ 故答案为：；‎ ‎【点睛】‎ 本题考查了频率分布直方图，意在考查学生的应用能力和计算能力.‎ ‎15．按下列程序框图运算：‎ 规定：程序运行到“判断结果是否大于”为次运算.若运算进行次才停止，则的取值范围是__________．‎ ‎【答案】‎ ‎【解析】根据题意得到不等式和，计算得到答案.‎ ‎【详解】‎ 根据题意知：且 故 故答案为：‎ ‎【点睛】‎ 本题考查了程序框图，没有考虑完整情况是容易发生的错误.‎ ‎16．已知、是椭圆和双曲线的公共焦点，是他们的一个公共点，且，则椭圆和双曲线的离心率的倒数之和的最大值为___.‎ ‎【答案】‎ ‎【解析】设|PF1|=r1，|PF2|=r2，|F1F2|=2c，椭圆和双曲线的离心率分别为e1，e2, 由余弦定理可得 ‎4c2=（r1）2+（r2）2﹣2r1r2cos，①在椭圆中，①化简为即4c2=4a2﹣3r1r2…②，在双曲线中，‎ 化简为即4c2=4a12+r1r2…③，，再利用柯西不等式求椭圆和双曲线的离 心率的倒数之和的最大值.‎ ‎【详解】‎ 设椭圆的长半轴为a，双曲线的实半轴为a1，（a＞a1），半焦距为c，‎ 由椭圆和双曲线的定义可知，‎ 设|PF1|=r1，|PF2|=r2，|F1F2|=2c，‎ 椭圆和双曲线的离心率分别为e1，e2,‎ ‎∵∠F1PF2=，则∴由余弦定理可得4c2=（r1）2+（r2）2﹣2r1r2cos，①‎ 在椭圆中，①化简为即4c2=4a2﹣3r1r2…②，‎ 在双曲线中，①化简为即4c2=4a12+r1r2…③，‎ ‎，‎ 由柯西不等式得（1+）（）≥（）2‎ 故答案为 ‎【点睛】‎ 本题主要考查椭圆和双曲线的定义和性质，利用余弦定理和柯西不等式是解决本题的关 键．属于难题．‎ 三、解答题 ‎17．在平面直角坐标系中，曲线的参数方程为(为参数)，以为极点，以轴的正半轴为极轴的极坐标系中，直线的极坐标方程为.‎ ‎(1)求曲线的极坐标方程；‎ ‎(2)设，直线与曲线相交于两点，求的值.‎ ‎【答案】 .‎ ‎【解析】(1)根据参数方程得到一般方程，再转化为极坐标方程得到答案.‎ ‎(2) 设直线的参数方程为：，代入圆方程，利用韦达定理得到，‎ ‎，再根据计算得到答案.‎ ‎【详解】‎ ‎(1) 则，即，故 ‎(2)设直线的参数方程为： ，‎ 代入圆方程得到 故，‎ ‎【点睛】‎ 本题考查了参数方程，极坐标方程，利用直线的参数方程解答问题简单，快捷，是解题的关键.‎ ‎18．随着智能手机的普及，使用手机上网成为了人们日常生活的一部分，很多消费者对手机流量的需求越来越大.长沙某通信公司为了更好地满足消费者对流量的需求，准备推出一款流量包.该通信公司选了5个城市（总人数、经济发展情况、消费能力等方面比较接近）采用不同的定价方案作为试点，经过一个月的统计，发现该流量包的定价:(单位：元/月）和购买人数(单位：万人）的关系如表:‎ 流量包的定价（元/月）‎ ‎30‎ ‎35‎ ‎40‎ ‎45‎ ‎50‎ 购买人数（万人）‎ ‎18‎ ‎14‎ ‎10‎ ‎8‎ ‎5‎ ‎（1）根据表中的数据，运用相关系数进行分析说明，是否可以用线性回归模型拟合与的关系？并指出是正相关还是负相关；‎ ‎（2）①求出关于的回归方程；‎ ‎②若该通信公司在一个类似于试点的城市中将这款流量包的价格定位25元/ 月，请用所求回归方程预测长沙市一个月内购买该流量包的人数能否超过20 万人.‎ 参考数据：，，.‎ 参考公式：相关系数，回归直线方程，其中，.‎ ‎【答案】(1)见解析;(2)①;②一个月内购买该流量包的人数会超过20万人.‎ ‎【解析】(1) 根据题意，得,计算出相关系数，从而可以作出判断;‎ ‎(2) ①求出回归直线方程，②由①知，若，则，从而预测长沙市一个月内购买该流量包的人数会超过20万人 ‎【详解】‎ ‎（1）根据题意，得，‎ ‎.‎ 可列表如下 根据表格和参考数据，得，‎ ‎.‎ 因而相关系数.‎ 由于很接近1，因而可以用线性回归方程模型拟合与的关系. ‎ 由于，故其关系为负相关.‎ ‎（2）①，，‎ 因而关于的回归方程为.‎ ‎②由①知，若，则，故若将流量包的价格定为25元/月，可预测长沙市一个月内购买该流量包的人数会超过20万人.‎ ‎【点睛】‎ 本题主要考查线性回归方程，属于难题.求回归直线方程的步骤：①依据样本数据画出散点图，确定两个变量具有线性相关关系；②计算的值；③计算回归系数；④写出回归直线方程为； 回归直线过样本点中心是一条重要性质，利用线性回归方程可以估计总体，帮助我们分析两个变量的变化趋势.‎ ‎19．如图，在三棱锥中，是边长为4的正三角形， ，分别为的中点，且.‎ ‎（1）证明：平面ABC；‎ ‎（2）求二面角的余弦值；‎ ‎（3）求点到平面的距离.‎ ‎【答案】（1）见解析（2）（3）‎ ‎【解析】（1）通过证明线线垂直即可得线面垂直.(2) 建立空间直角坐标系，求出两平面法向量的坐标，求其夹角即可.(3)为平面的一个法向量,点B到平面SCM的距离d=即可得解.‎ ‎【详解】‎ ‎（1）证明：取线段的中点，连接.‎ 因为，，所以且 SO⊥AB，‎ 所以平面.‎ ‎（2）建立如图所示空间直角坐标系,则,‎ 为平面的一个法向量. ‎ 由（1）得：，.‎ 设为平面的一个法向量，则 即 取 ，则 ‎ 所以 由图可知：二面角是锐角二面角，‎ 所以二面角的余弦值为. ‎ ‎（3）由（1）（2）可得：，为平面的一个法向量.‎ 所以，点到平面的距离 点睛:本题考查了线面垂直的判定定理,二面角的求法以及点到面的距离,熟记定理内容是关键,应用建系解决空间角及距离是常用方法,注意计算的准确性.‎ ‎20．已知.‎ 解不等式：；‎ 若不等式对任意恒成立，求的取值范围.‎ ‎【答案】（1）（2）‎ ‎【解析】（1）讨论，，三种情况，分别计算得到答案.‎ ‎（2）讨论和两种情况，得到，利用绝对值三角不等式得到，计算得到答案.‎ ‎【详解】‎ ‎ ①‎ ‎②‎ ‎③‎ 由可得;‎ ‎①当时，;‎ ‎②当时，即对恒成立，‎ ‎，当且仅当，即时取等号，‎ ‎，解得.‎ ‎【点睛】‎ 本题考查了解绝对值不等式，不等式恒成立问题，意在考查学生的综合应用能力.‎ ‎21．已知抛物线的顶点在原点，对称轴是轴，且过点.‎ ‎（Ⅰ）求抛物线的方程；‎ ‎（Ⅱ）已知斜率为的直线交轴于点，且与曲线相切于点，点在曲线上，且直线轴，关于点的对称点为，判断点是否共线，并说明理由.‎ ‎【答案】(Ⅰ)；(Ⅱ)答案见解析.‎ ‎【解析】试题分析：‎ ‎(Ⅰ)设抛物线的标准方程为，结合抛物线过点可得抛物线的方程为.‎ ‎(Ⅱ)设直线，联立直线方程与抛物线方程可得，由判别式等于零可得，即，，，，整理计算可得点A的坐标为，由于，故点共线.‎ 试题解析：‎ ‎(Ⅰ)根据题意，可设抛物线的标准方程为，‎ 所以，解得，‎ 所以抛物线的方程为.‎ ‎(Ⅱ)点共线，理由如下：‎ 设直线，联立 得()‎ 由，解得，‎ 则直线，得，，‎ 又关于点的对称点为，故，‎ 此时，()可化为，解得，‎ 故，即，‎ 所以，即点共线.‎ 点睛：直线与抛物线的位置关系和直线与椭圆、双曲线的位置关系类似，一般要用到根与系数的关系.‎ ‎22．已知椭圆的方程为，圆与轴相切于点，与轴正半轴相交于、两点，且，如图1.‎ ‎（1）求圆的方程；‎ ‎（2）如图1，过点的直线与椭圆相交于、两点，求证：射线平分；‎ ‎（3）如图2所示，点、是椭圆的两个顶点，且第三象限的动点在椭圆上，若直线与轴交于点，直线与轴交于点，试问：四边形的面积是否为定值？若是，请求出这个定值，若不是，请说明理由.‎ ‎【答案】（1）；（2）证明见解析；（3）是，.‎ ‎【解析】（1）根据已知条件设出圆心坐标,半径为圆心纵坐标,利用弦长公式,可求出圆的方程;‎ ‎（2）先求出点坐标,设出直线方程,与椭圆方程联立,利用韦达定理,即可求得,命题得证;‎ ‎（3）设,求出直线、直线方程，进而求出点与点的坐标,然后四边形的面积用点与点的坐标表示,计算可得定值.‎ ‎【详解】‎ ‎（1）依题意,设圆心，‎ ‎，解得 所求的方程为;‎ ‎（2）代入圆方程，得或 若过点的直线斜率不存在,此时在轴上,‎ ‎,射线平分,‎ 若过点的直线斜率存在，设其方程为 联立，消去得,‎ 设,,‎ ‎,‎ ‎,‎ 射线平分,‎ ‎（3）设,‎ 直线方程为,令 得，即,‎ 直线方程为,令 得，即,,‎ ‎,‎ 四边形的面积为定值.‎ ‎【点睛】‎ 本题考查了圆的标准方程求法,直线与圆锥曲线相交问题韦达定理的应用,以及定值问题,是综合类题目,考虑到证两条直线的斜率互为相反数是解决问题的关键,属于难题.‎