2020届二轮复习函数与基本初等函数(三)学案(全国通用)
年 级: 辅导科目:数学 课时数:
课 题
函数与基本初等函数(三)
教学目的
教学内容
第五节 指数与指数函数
(一)高考目标
考纲解读
1.了解指数函数模型的实际背景.
2.理解有理数指数幂的含义,了解实数指数幂的意义,掌握幂的运算.
3.理解指数函数的概念,理解指数函数的单调性,掌握指数函数图像通过的特殊点.
4.知道指数函数是一类重要的函数模型.
考向预测
1.指数函数在高中数学中占有十分重要的地位,是高考重点考查的对象,热点是指数函数的图像与性质的综合应用.同时考查分类整合思想和数形结合思想.
2.幂的运算是解决与指数有关问题的基础,常与指数函数交汇命题.
(二)课前自主预习
知识梳理
1.指数幂的概念
(1)根式
如果一个数的n次方等于a(n>1且n∈N+),那么这个数叫做a的n次方根.也就是,若xn=a,则x叫
做 ,其中n>1且n∈N+.式子 叫做 ,这里n叫做 ,a叫做 .
(2)根式的性质
①当n为奇数时,正数的n次方根是一个正数,负数的n次方根是一个负数,这时,a的n次方根用符号 表示.
②当n为偶数时,正数的n次方根有两个,它们互为相反数,这时,正数的正的n次方根用符号 表示,负的n次方根用符号 - 表示.正负两个n次方根可以合写为± (a>0).
③()n= .
④当n为奇数时,= ;
当n为偶数时,=|a|= .
⑤负数没有偶次方根.
⑥零的任何次方根都是零.
2.有理数指数幂
(1)分数指数幂的表示
①正数的正分数指数幂是
= (a>0,m,n∈N+,n>1).
②正数的负分数指数幂是
= = (a>0,m,n∈N+,n>1).
③0的正分数指数幂是 ,0的负分数指数幂无意义.
(2)有理数指数幂的运算性质
①aras= (a>0,r,s∈Q).
②(ar)s= (a>0,r,s∈Q).
③(ab)r= (a>0,b>0,r∈Q).
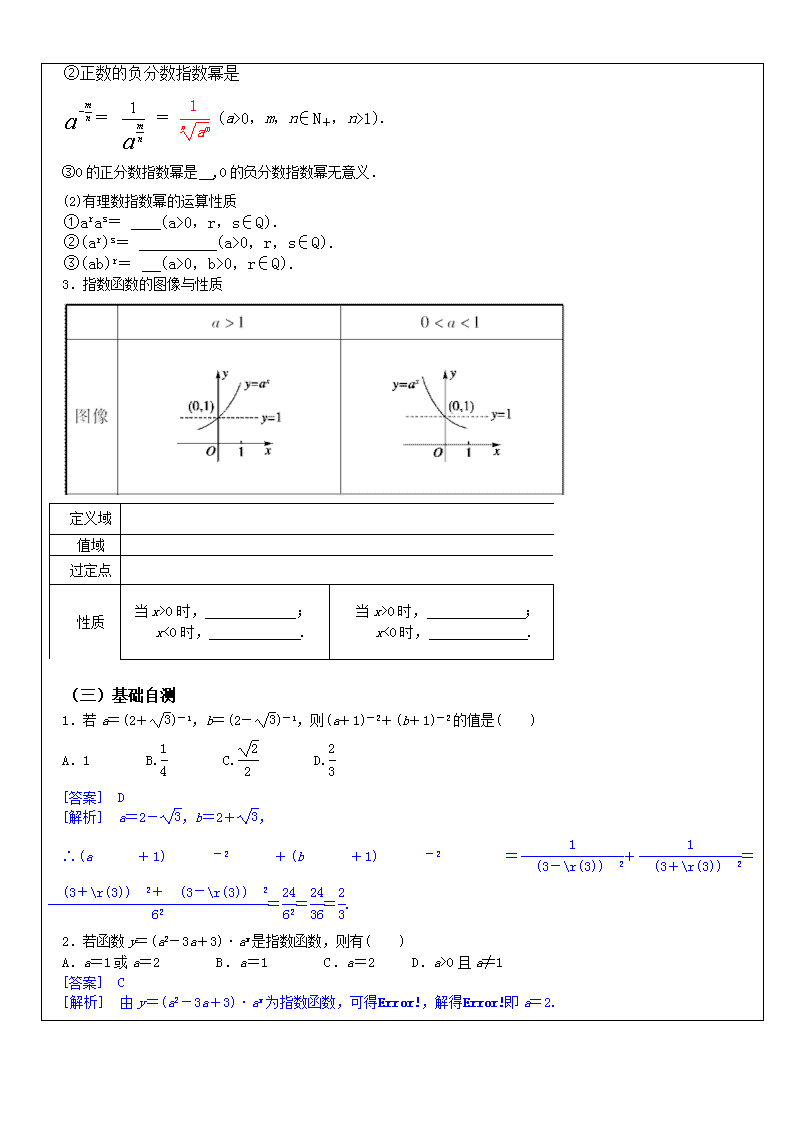
3.指数函数的图像与性质
定义域
值域
过定点
性质
当x>0时, ;
x<0时, .
当x>0时, ;
x<0时, .
(三)基础自测
1.若a=(2+)-1,b=(2-)-1,则(a+1)-2+(b+1)-2的值是( )
A.1 B. C. D.
[答案] D
[解析] a=2-,b=2+,
∴(a+1)-2+(b+1)-2=+====.
2.若函数y=(a2-3a+3)·ax是指数函数,则有( )
A.a=1或a=2 B.a=1 C.a=2 D.a>0且a≠1
[答案] C
[解析] 由y=(a2-3a+3)·ax为指数函数,可得,解得即a=2.
3.(2018·东营模拟)函数y=的单调递增区间是( )
A.(-∞,-1] B.[2,+∞) C. D.
[答案] D
[解析] 令t=-x2+x+2≥0,得函数定义域为[-1,2],所以t=-x2+x+2在上递增,在上递减.根据“同增异减”的原则,函数y=的单调递增区间是.
4.函数f(x)=则f(-3)=__________.
[答案] .
[解析] f(-3)=f(-3+2)=f(-1)=f(-1+2)=f(1)=f(1+2)=f(3)=2-3=.
5.(2009·江苏文)已知a=,函数f(x)=ax,若实数m,n满足f(m)>f(n),则m,n的大小关系为________
[答案] m
f(n),
∴m0),则log a=
[答案] 3
2.命题方向:指数函数性质的考查
[例2] 求下列函数的定义域和值域.
(1)y=-|x+1|;(2)y=;(3)y=2
[分析] 指数函数y=ax(a>0,a≠1)的定义域为R,所以y=af(x)的定义域与f(x)定义域相同;值域则要应用其单调性来求,复合函数则要注意“同增异减”的原则.
[解析] (1)定义域为R.因为-|x+1|≤0,
所以y=-|x+1|≥0=1,所以值域为[1,+∞).
(2)因为2x+1>0恒成立,所以定义域为R.又因为y==1-,而0<<1,所以-1<-<0,
解得00且a≠1).
(1)求函数f(x)的定义域;
(2)讨论f(x)的奇偶性;
(3)求a的取值范围,使f(x)>0在定义域上恒成立.
[分析] 问题的关键是考查+具有哪些性质,因x3对任意x∈R均有意义,其奇偶性易于考查.
[解析] (1)由于ax-1≠0,则ax≠1,得x≠0,
所以函数f(x)的定义域为{x|x≠0,x∈R}.
(2)对于定义域内任意x,有
f(-x)=(-x)3=(-x3)=(-x)3=x3=f(x).
∴f(x)是偶函数.
(3)当a>1时,对x>0,由指函数的性质知ax>1,
∴ax-1>0,+>0,
又x>0时,x3>0,
∴x3>0,
即当x>0时,f(x)>0.
又由(2),f(x)为偶函数,知f(-x)=f(x),
当x<0时,-x>0,有f(-x)=f(x)>0成立.
综上知a>1时,f(x)>0在定义域上恒成立.
对于00时,1>ax>0,ax+1>0,ax-1<0,x3>0,
此时f(x)<0,不满足题意;
当x<0时,-x>0,f(-x)=f(x)<0,也不满足题意.
[点评] (1)判定此类函数的奇偶性,常需要对所给式子变形,以达到所需要的形式,另外,还可利用求
f(-x)±f(x)来判断.
(2)可借助函数的奇偶性,研究函数的其他性质,这样做的好处是避免了自变量取值的讨论.
综上,所求a的范围是a>1.
3.命题方向:指数函数的图像应用
[例3] 已知函数y=|x+1|.
(1) 作出图像;(2)由图像指出其单调区间;(3)由图像指出当x取什么值时有最值.
[分析]
[解析] (1)解法1:由函数解析式可得
y=|x+1|=
其图像由两部分组成:
一部分是:y=x(x≥0)y=x+1(x≥-1);
另一部分是:y=3x(x<0)y=3x+1(x<-1).
如图:
解法2:①由y=|x|可知函数是偶函数,其图像关于y轴对称,故先作出y=x的图像保留x≥0的部分,
当x<0时,其图像是将y=x(x≥0)图像关于y轴对折,从而得出y=|x|的图像.
②将y=|x|向左移动1个单位,即可得y=|x+1|的图像,如图所示.
(2)由图像知函数在(-∞,-1]上是增函数,在[-1,+∞)上是减函数.
(3)由图像知当x=-1时,有最大值1,无最小值.
跟踪练习3:
已知实数a、b满足等式a=b,下列五个关系式:①00时,a=b,则有00且a≠1).
(1)判断f(x)的奇偶性;
(2)讨论f(x)的单调性;
(3)当x∈[-1,1]时,f(x)≥b恒成立,求b的取值范围.
[分析] (1)首先看函数的定义域,而后用奇偶性定义判断;(2)单调性利用复合函数单调性易于判断,还可用导数解决;(3)恒成立问题关键是探求f(x)的最小值
[解析] (1)函数定义域为R,关于原点对称.
又∵f(-x)=(a-x-ax)=-f(x),
∴f(x)为奇函数.
(2)当a>1时,a2-1>0,
y=ax为增函数,y=a-x为减函数,从而y=ax-a-x为增函数,∴f(x)为增函数.
当00,且a≠1时,f(x)在定义域内单调递增.
(3)由(2)知f(x)在R上是增函数,
∴在区间[-1,1]上为增函数.
∴f(-1)≤f(x)≤f(1).
∴f(x)min=f(-1)=(a-1-a)=·=-1.
∴要使f(x)≥b在[-1,1]上恒成立,则只需b≤-1.
故b的取值范围是(-∞,-1].
[点评] (1)函数奇偶性与单调性是高考考查的热点问题,常以指数函数为载体考查函数的性质与恒成立问题.
(2)求参数的范围也是常考内容,难度不大,但极易造成失分,因此对题目进行认真分析,必要的过程不可少,这也是高考阅卷中十分强调的问题.
跟踪练习4:
已知函数f(x)=a2x+2ax-1(a>0,且a≠1)在区间[-1,1]上的最大值为14,求实数a的值.
[解析] f(x)=a2x+2ax-1=(ax+1)2-2,
∵x∈[-1,1],
(1)当01时,≤ax≤a,
∴当ax=a时,f(x)取得最大值.
∴(a+1)2-2=14,∴a=3.
综上可知,实数a的值为或3.
(五)思想方法点拨:
1.单调性是指数函数的重要性质,特别是函数图像的无限伸展性,x轴是函数图像的渐近线.当01时,x→-∞,y→0;当a>1时,a的值越大,图像越靠近y轴,递增的速度越快;当01,b>0,且ab+a-b=2,则ab-a-b的值等于( )
A. B.2或-2 C.-2 D.2
[答案] D
[解析] ∵a>1,b>0,∴ab>a-b.
又∵ab+a-b=2,
∴(ab+a-b)2=a2b+a-2b+2=8,
∴(ab-a-b)2=a2b+a-2b-2=4,∴ab-a-b=2.
2.若函数y=ax+b-1 (a>0,且a≠1)的图像经过第二、三、四象限,则一定有( )
A.00 B.a>1,且b>0
C.01,且b<0
[答案] C
[解析] 如图所示,图像与y轴的交点在y轴的负半轴上,即a0+b-1<0,
∴b<0,又图像经过第二、三、四象限,
∴0f(a)>f(b),则下列关系式中一定成立的是( )
A.3c>3b B.3b>3a C.3c+3a>2 D.3c+3a<2
[答案] D
[解析] 作f(x)=|3x-1|的图像如图所示,由图可知,
要使cf(a)>f(b)成立,
则有c<0且a>0,
∴3c<1<3a,
∴f(c)=1-3c,f(a)=3a-1.
又f(c)>f(a),∴1-3c>3a-1,
即3a+3c<2,故选D.
4.函数的y=3x图像与函数y=x-2的图像关于( )
A.点(-1,0)对称 B.直线x=1对称
C.点(1,0)对称 D.直线x=-1对称
[答案] B
[解析] y=3xy=xy=x-2,在同一坐标系中作出y=3x,y=3x-2图像,结合选项知选B.
5.函数y=ax在[0,1]上的最大值与最小值的和为3,则a的值为( )
A. B.2 C.4 D.
[答案] B
[解析] 当a>0,a≠1时,y=ax是定义域上的单调函数,因此其最值在x∈[0,1]的两个端点得到,
于是必有1+a=3,∴a=2.
6.若函数y=4x-3·2x+3的定义域为集合A,值域为[1,7],集合B=(-∞,0]∪[1,2],则集合A与集合B的关系为( )
A.AB B.A=B C.BA D.A⊆B
[答案] A
[解析] ∵y=2+的值域为[1,7],
∴2x∈[2,4].
∴x∈[1,2],即A=[1,2].∴AB.
7.(2018·陕西文)下列四类函数中,具有性质“对任意的x>0,y>0,函数f(x)满足f(x+y)=f(x)f(y)”的是( )
A.幂函数 B.对数函数 C.指数函数 D.余弦函数
[答案] C
[解析] 本题考查幂函数,指数函数、对数函数、余弦函数的性质.对任意的x>0,y>0,
只有指数函数f(x)满足f(x+y)=f(x)·f(y).
8.(2018·济宁模拟)已知函数f(x)满足:当x≥4时,f(x)=x;当x<4时,f(x)=f(x+1),则f(2+log23)=( )
A. B. C. D.
[答案] A
[解析] ∵2<3<4=22,
∴10且a≠1)的图像有两个公共点,则a的取值范围是________.
[答案]
[解析] 数形结合.由图可知0<2a<1,
作出01两种图像易知只有00,且a≠1).
考向预测
1.对数运算是高中学习的一种重要运算,而对数函数又是最重要的一类基本初等函数,因此该节内容是高考的重点.
2.考查热点是对数式的运算和对数函数的图像、性质的综合应用,同时考查分类整合、数形结合、函数与方程思想.
3.常以小题的形式考查对数函数的图像、性质,或与其他知识交汇以解答题的形式出现.
(二)课前自主预习
知识梳理
1.对数的概念
(1)对数的定义
如果 ,那么数b叫做以a为底N的对数,记作 .其中 叫做对数的底数, 叫做真数.
(2)几种常见对数
对数形式
特点
记法
一般对数
底数为a(a>0且a≠1)
.
常数对数
底数为 .
.
自然对数
底数为 .
.
2.对数的性质与运算法则
(1)对数的性质
①alogaN= ;②logaaN= (a>0且a≠1).
(2)对数的重要公式
①换底公式: logbN= (a,b均大于零且不等于1);
②logab=,推广logab·logbc·logcd= .
(3)对数的运算法则
如果a>0且a≠1,M>0,N>0,那么
①loga(MN)= ;
②loga= ;
③logaMn= (n∈R);
④logamMn=logaM.
3.对数函数的图像与性质
a>1
01时, .
当01时, .
当00,且a≠1)的反函数,其图像经过点(,a),则f(x)=( )
A.log2x B. C. D.x2
[答案] B
[解析] 考查反函数的概念,指对函数的关系及对数的运算性质.函数y=ax的反函数是f(x)=logax,
∵其图像经过点(,a),∴a=loga,∴a=,
∴f(x)=
4.已知f(x)=|logax|(0f >f B.f >f(2)>f
C.f >f(2)>f D.f >f >f(2)
[答案] D
[解析] ∵0loga>loga>0.
又loga=-loga2,∴|loga|=|loga2|,
∴|loga|>|loga|>|loga2|,
即f >f >f(2).
5.[(1-log63)2+log62·log618]÷log64=________.
[答案] 1
[解析] 原式=[(log62)2+log62·(1+log63)]÷2log62
=[(log62)2+log62+log62·log63]÷2log62=log62++log63=log6(2×3)+=+=1.
6.设f(x)=则满足f(x)=的x值为__________.
[答案] 3
[解析] 当x≤1时,令2-x=,则x=2,不合题意;
当x>1时,令log81x=,则x=81=3.
综上,x=3.
7.已知定义域为R的函数f(x)为奇函数,且满足f(x+2)=-f(x),当x∈[0,1]时,f(x)=2x-1.
(1)求f(x)在[-1,0)上的解析式;
(2)求f(log 24).
[解析] (1)令x∈[-1,0),则-x∈(0,1],
∴f(-x)=2-x-1.又∵f(x)是奇函数,
∴f(-x)=-f(x),
∴-f(x)=f(-x)=2-x-1,
∴f(x)=-x+1.
(2)∵log24=-log224∈(-5,-4),
∴log24+4∈(-1,0),
∵f(x+2)=-f(x),
∴f(x+4)=-f(x+2)=f(x),
∴f(x)是以4为周期的周期函数,
∴f(log24)=f(log24+4)=-log24+4+1=-24·+1=-.
(四)典型例题
1.命题方向:对数的运算
[例1] 求值:
(1)2(lg)2+lg·lg5+;
(2)31+log36-24+log23+103lg3+log34-1;
(3)(lg2)3+(lg5)3+3lg2·lg5.
[分析] 灵活运用公式和性质进行计算,注意公式的逆用.
[解析] (1)原式=lg(2lg+lg5)+=lg(lg2+lg5)+1-lg=lg+1-lg=1.
(2)原式=3·3log36-16·2log23+10lg27+32-log316=18-48+27+=-.
(3)原式=(lg2+lg5)[(lg2)2-lg2·lg5+(lg5)2]+3lg2·lg5
=(lg2)2-lg2·lg5+(lg5)2+3lg2·lg5=(lg2+lg5)2=1.
[点评] 对数运算中注意逆用对数运算法则,若对数运算中出现不同的底,注意利用换底公式统一“底”,再进行运算.
跟踪练习1
计算下列各题:
(1); (2)log3log5[log210-(3)-7log72].
[解析] (1)原式===1.
(2)原式=log3·log5[2log210-(3)-7log72]
=·log5(10-3-2)=·log55=-.
2.命题方向:对数的概念及运算性质
[例2] 已知x、y、z为正数,
(1)求使2x=py的p的值;
(2)求与(1)中所求的p的差最小的整数;
(3)求证=
(4)比较3x,4y,6z的大小.
[解析] (1)设3x=4y=6z=k(显然k≠1),
则x=log3k,y=log4k,z=log6k.
由2x=py得2log3k=plog4k=p·,
∵log3k≠0,∴p=2log34.
(2)p=2log34=log316,∴2,∴p-2>3-p,故与p的差最小的整数是3.
(3)证明:-=-=logk6-logk3=logk2=logk4==.
(4)∵k>1,∴lgk>0
3x-4y=(lg64-lg81)<0,
4y-6z=(lg36-lg64)<0,
∴3x<4y<6z.
[点评] 本题的解答利用了ax=N(a>0且a≠1)⇔x=logaN,即指数式与对数式的互化,另外,在分析该题时,可
用方程思想作指导,将条件中的等式看作是关于x,y,z的方程组.
跟踪练习2
(1)若2a=5b=10,求+的值;
(2)若xlog34=1,求4x+4-x的值.
[解析] (1)由已知a=log210,b=log510,
则+=lg2+lg5=lg10=1.
(2)由已知x=log43
则4x+4-x=4log43+4-log43=3+=.
3.命题方向:对数函数的图像与性质
[例3] 已知函数f(x)=loga(2-ax),是否存在实数a,使函数f(x)在[0,1]上是x的减函数,若存在,求a的取值范围.
[分析] 参数a既出现在底数上,又出现在真数上,应全面审视对a的取值范围的制约.
[解析] ∵a>0,且a≠1,
∴u=2-ax是x的减函数.
又f(x)=loga(2-ax)在[0,1]是减函数,
∴函数y=logau是u的增函数,且对x∈[0,1]时,
u=2-ax恒为正数.
其充要条件是 即11,
在区间(-∞,1-]上是减函数,
所以g(x)=x2-ax-a在区间(-∞,1-]上也是单调减函数,且g(x)>0.
∴,即.
解得2-2≤a<2.
(五)思想方法点拨
1.指数式ab=N与对数式logaN=b的关系以及这两种形式的互化是对数运算法则的关键.
2.在运用性质logaMn=nlogaM时,要特别注意条件,在无M>0的条件下应为logaMn=nloga|M|(n∈N*且n为偶数).
3.注意对数恒等式、对数换底公式及等式logambn=·logab,logab=在解题中的灵活应用.
4.指数函数y=ax与对数函数y=logax(a>0,且a≠1)互为反函数,要能从概念、图像和性质三个方面理解它们之间的联系与区别.
5.比较两个幂值的大小是一种常见的题型,也是一类容易做错的题目.解决这类问题时,首先要分清是底数相同还是指数相同.如果底数相同,可利用指数函数的单调性;如果指数相同,可利用图像(如下表).
同一坐标系下的图像关系
当底大于1时,底越大,图像越靠近坐标轴;当底小于1大于0时,底越小,图像靠近坐标轴,如果底数、指数都不同,则要利用中间变量.
(六)课后强化作业
一、选择题
1.(2018·四川文)函数y=log2x的图像大致是( )
A B C D
[答案] C
[解析] 考查对数函数的图像.
2.(2018·天津理)设函数f(x)=若f(a)>f(-a),则实数a的取值范围是( )
A.(-1,0)∪(0,1) B.(-∞,-1)∪(1,+∞)
C.(-1,0)∪(1,+∞) D.(-∞,-1)∪(0,1)
[答案] C
[解析] 当a>0时,由f(a)>f(-a)得,log2a>loga,∴a>1;当a<0时,由f(a)>f(-a)得,
log(-a)>log2(-a),∴-1b>c>0,则、、的大小关系是( )
A.>> B.>>
C.>> D.>>
[答案] B
[解析] ∵、、可看作函数图像上的点与原点所确定的直线的斜率,结合函数f(x)=log2(x+1)的图像及a>b>c>0可知>>.故选B.
5.已知logx1=logax2=loga+1x3>0,00,画出图像后知选D.
6.设函数f(x)=loga(x+b)(a>0且a≠1)的图像过点(2,1),其反函数的图像过点(2,8),则a+b等于( )
A.6 B.5 C.4 D.3
[答案] C
[解析] 由题意得解得a=3,b=1.
于是a+b=4,选C.
[点评] 反函数的图像和原函数的图像关于直线y=x对称.点P(a,b)在原函数y=f(x)的图像上⇔点P′(b,a)在反函数y=g(x)的图像上.解答该题是不需要求出反函数的.
7.(2018·全国卷Ⅰ理)设a=log32,b=ln2,c=5-,则( )
A.alog2e>1,所以a2=log24>log23,所以c0)的图像关于直线y=x对称,则f(x)=________.
[答案] 3x(x∈R)
[解析] y=f(x)是函数y=log3x(x>0)的反函数.
11.已知函数f(x)=2x,等差数列{an}的公差为2,若f(a2+a4+a6+a8+a10)=4,
则log2[f(a1)·f(a2)·f(a3)·…·f(a10)]=________.
[答案] -6
[解析] ∵f(a2+a4+a6+a8+a10)=4,f(x)=2x,
∴a2+a4+a6+a8+a10=2,
∵{an}为公差d=2的等差数列,
∴a1+a2+…+a10=2(a2+a4+a6+a8+a10)-5d=-6.
∴log2[f(a1)·f(a2)·…·f(a10)]=log2[2a1·2a2·…·2a10]=log22a1+a2+…+a10=-6.