- 2021-07-01 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高一三角函数试题及答案:正弦函数、余弦函数的图象和性质
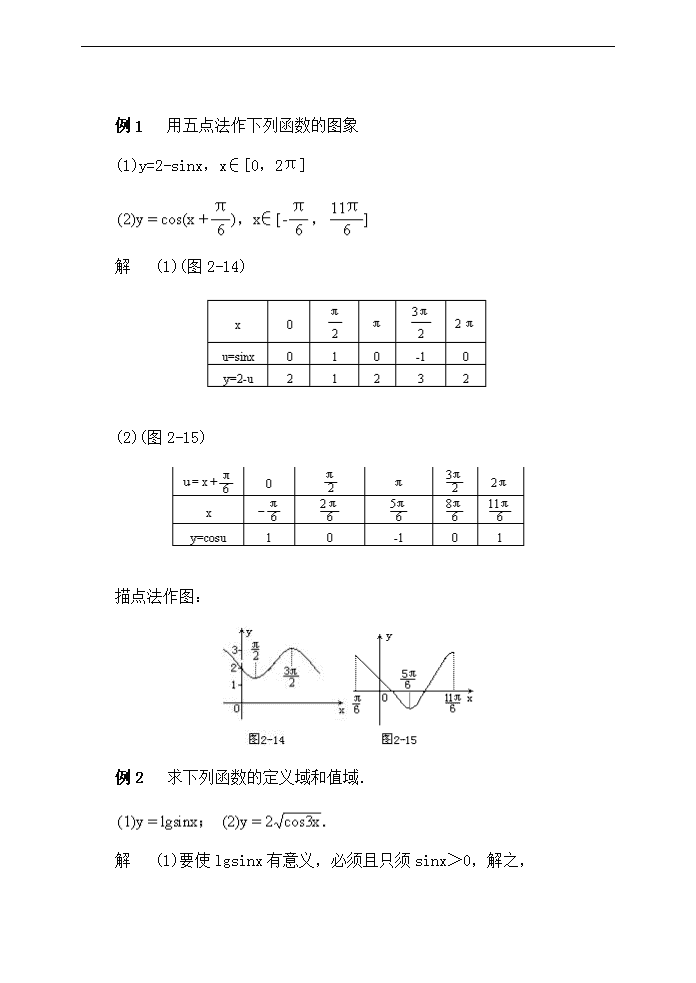
例1 用五点法作下列函数的图象 (1)y=2-sinx,x∈[0,2π] 解 (1)(图2-14) (2)(图2-15) 描点法作图: 例2 求下列函数的定义域和值域. 解 (1)要使lgsinx有意义,必须且只须sinx>0,解之, 得 2kπ<x<(2k+1)π,k∈Z. 又∵0<sinx≤1, ∴-∞<lgsinx≤0. ∴定义域为(2kπ,(2k+1)π)(k∈Z),值域为(-∞,0]. 的取值范围,进而再利用三角函数线或函数图象,求出x的取值范围。 利用单位圆(或三角函数图象)解得 (2)由读者自己完成,其结果为 例4 求下列函数的最大值与最小值: (2)y=2cos2x+5sinx-4=-2sin2x+5sinx-2 ∵sinx∈[-1,1], 例5 求下列函数的值域. ∵|cosx|≤1 ∴cox2x≤1 说明 上面解法的实质是从已知关系式中,利用|cosx|≤1消去x,从而求出y的范围. 例6 比较下列各组数的大小. 分析 化为同名函数,进而利用增减性来比较函数值的大小. 解 (1)sin194°=sin(180°+14°)=-sin14° cos160°=cos(180°-20°)=-cos20°=-sin70° ∵0<14°<70°<90°, ∴sin14°<sin70°,从而 -sin14°>-sin70°,即 sin194°>cos160°. 而y=cosx在[0,π]上是减函数, 故由0<1.39<1.47<1.5<π可得 cos1.5<cos1.47<cos1.39 例7 求下列函数的单调区间 解(1)设u=2x 当u∈[(2k-1)π,2kπ](k∈Z)时,cosu递增; 当u∈[2kπ,(2k+1)π](k∈Z)时,cosu递减. 例8 下列函数中是奇函数的为 ∴(D)为奇函数,应选(D). 函数不具有奇偶性. 说明 奇(偶)函数的定义域必须对称于原点,这是奇(偶)函数必须满足的条件,解题时不可忽视.查看更多