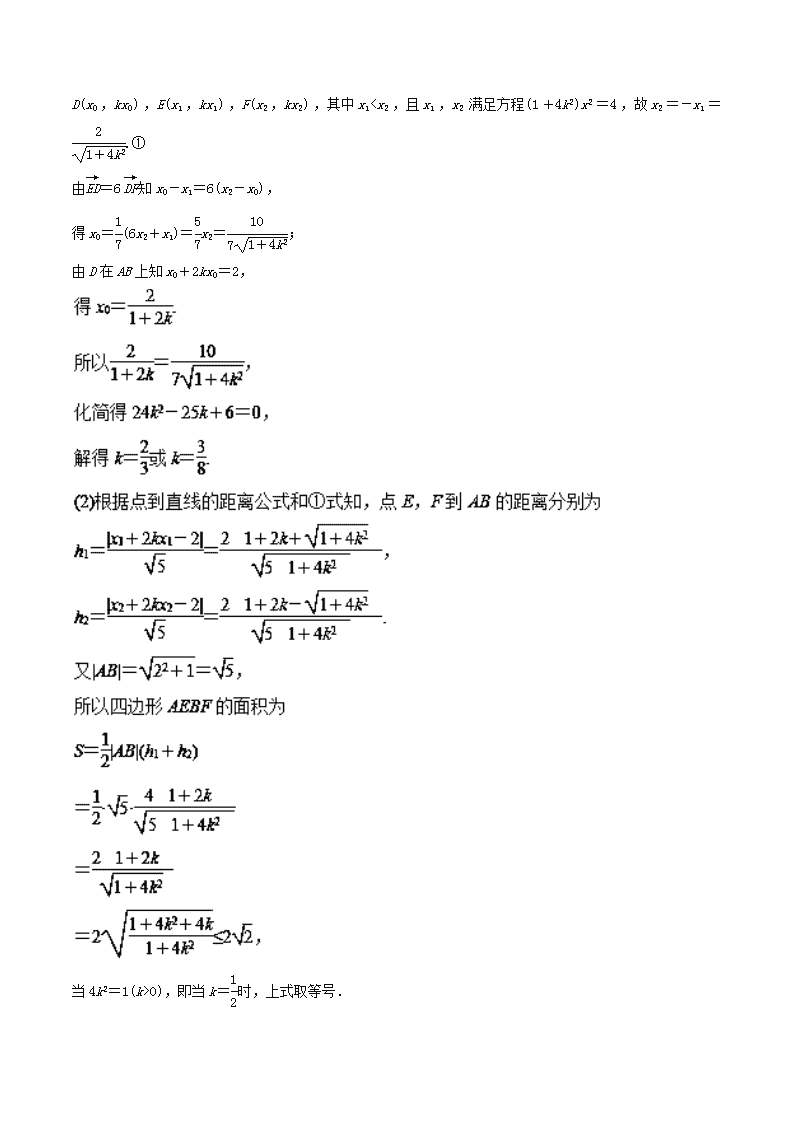专题22 数学思想方法(押题专练)-2018年高考文数二轮复习精品资料
1、如果方程cos2x-sinx+a=0在(0,]上有解,求a的取值范围.
因此f(t)=0在(0,1]上有解等价于
即所以-1
0)与AB相交于点D,与椭圆相交于E、F两点.
(1)若=6,求k的值;
(2)求四边形AEBF面积的最大值.
解 (1)依题意得椭圆的方程为+y2=1,直线AB,EF的方程分别为x+2y=2,y=kx(k>0).如图,设D(x0,kx0),E(x1,kx1),F(x2,kx2),其中x10),即当k=时,上式取等号.
所以S的最大值为2.
即四边形AEBF面积的最大值为2.
5.设a,b∈R且b≠0,若复数(a+bi)3是实数,则a、b满足的关系式为________.
【答案】b2=3a2
【解析】(a+bi)3=(a+bi)2(a+bi)
=a3+3a2bi-3ab2-b3i
=(a3-3ab2)+(3a2b-b3)i,
因(a+bi)3是实数且b≠0,
所以3a2b-b3=0⇒b2=3a2.
6.满足条件AB=2,AC=BC的三角形ABC的面积的最大值是________.
【答案】2
【解析】可设BC=x,则AC=x,
根据面积公式得S△ABC=x,
由余弦定理计算得cosB=,
代入上式得S△ABC=x
=.
由得2-21,若仅有一个常数c使得对于任意的x∈[a,2a],都有y∈[a,a2]满足方程logax+logay=c,这时,a的取值的集合为________.
【答案】{2}
8.已知直线y=a交抛物线y=x2于A,B两点.若该抛物线上存在点C,使得∠ACB为直角,则a
的取值范围为________.
【答案】[1,+∞)
【解析】以AB为直径的圆的方程为x2+(y-a)2=a,
由
得y2+(1-2a)y+a2-a=0.
即(y-a)[y-(a-1)]=0,
则由题意得解得a≥1.
9.已知f(x)是定义域为R的偶函数,当x≥0时,f(x)=x2-4x,那么,不等式f(x+2)<5的解集是________.
【答案】{x|-70,∵x≥0时,f(x)=x2-4x,∴f(-x)=(-x)2-4(-x)=x2+4x,又f(x)为偶函数,∴f(-x)=f(x),∴x<0时,f(x)=x2+4x,故有f(x)=再求f(x)<5的解,由得0≤x<5;由得-5b>0)的一个顶点为A(2,0),离心率为.直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为时,求k的值.
解 (1)由题意得解得b=.
所以椭圆C的方程为+=1.
(2)由得(1+2k2)x2-4k2x+2k2-4=0.
设点M,N的坐标分别为(x1,y1),(x2,y2),
则x1+x2=,
x1x2=.
所以MN=
=
=.
又因为点A(2,0)到直线y=k(x-1)的距离
d=,
所以△AMN的面积为
S=MN·d=.
由=,解得k=±1.
所以,k的值为1或-1.
13.设关于θ的方程cosθ+sinθ+a=0在区间(0,2π)内有相异的两个实根α、β.
(1)求实数a的取值范围;
(2)求α+β的值.
14.设有函数f(x)=a+和g(x)=x+1,已知x∈[-4,0]时恒有f(x)≤g(x),求实数a的取值范围.
15. 已知函数f(x)=x3-3ax-1,a≠0.
(1)求f(x)的单调区间;
(2)若f(x)在x=-1处取得极值,直线y=m与y=f(x)的图象有三个不同的交点,求m的取值范围.
解 (1)f′(x)=3x2-3a=3(x2-a),
当a<0时,对x∈R,有f′(x)>0,
∴当a<0时,f(x)的单调增区间为(-∞,+∞);
当a>0时,由f′(x)>0,解得x<-或x>,
由f′(x)<0,解得-0时,f(x)的单调增区间为(-∞,-),(,+∞);单调减区间为(-,).
(2)∵f(x)在x=-1处取得极值,
16.已知实数x,y满足则的最大值为________.
【答案】2
【解析】画出不等式组
对应的平面区域Ω为图中的四边形ABCD,=表示的平面区域Ω上的点P(x,y)与原点的连线的斜率,显然OA的斜率最大.
17.已知P是直线l:3x+4y+8=0上的动点,PA、PB是圆x2+y2-2x-2y+1=0的两条切线,A、B是切点,C是圆心,求四边形PACB面积的最小值.
解
18.已知抛物线y2=2px(p>0)的焦点为F,A是抛物线上横坐标为4,且位于x轴上方的点,A到抛物线准线的距离等于5,过A作AB垂直于y轴,垂足为B,OB的中点为M.
(1)求抛物线的方程;
(2)以M为圆心,MB为半径作圆M,当K(m,0)是x轴上一动点时,讨论直线AK与圆M的位置关系.
解 (1)抛物线y2=2px的准线为x=-,
由题意得4+=5,所以p=2,
所以抛物线的方程为y2=4x.
(2)由题意知,圆M的圆心为点(0,2),半径为2.
当m=4时,直线AK的方程为x=4,
此时,直线AK与圆M相离;
当m≠4时,由(1)知A(4,4),
则直线AK的方程为y=(x-m),
即4x-(4-m)y-4m=0,
圆心M(0,2)到直线AK的距离
d=,
令d>2,解得m>1.
所以,当m>1时,直线AK与圆M相离;
当m=1时,直线AK与圆M相切;
当m<1时,直线AK与圆M相交.
19.设关于x的函数y=2cos2x-2acosx-(2a+1)的最小值为f(a),试确定满足f(a)=的a的值,并求此时函数的最大值.
20.已知a是实数,函数f(x)=(x-a).
(1)求函数f(x)的单调区间;
(2)设g(a)为f(x)在区间[0,2]上的最小值.
①写出g(a)的表达式;
②求a的取值范围,使得-6≤g(a)≤-2.
解 (1)函数的定义域为[0,+∞),
f′(x)=+=(x>0).
21.已知等差数列{an}的前3项和为6,前8项和为-4.
(1)求数列{an}的通项公式;
(2)设bn=(4-an)qn-1 (q≠0,n∈N*),求数列{bn}的前n项和Sn.
解 (1)设数列{an}的公差为d,
由已知,得解得
故an=3-(n-1)=4-n.
(2)由(1)可得bn=n·qn-1,
于是Sn=1·q0+2·q1+3·q2+…+n·qn-1.
若q≠1,将上式两边同时乘以q,得
qSn=1·q1+2·q2+…+(n-1)·qn-1+n·qn.
两式相减,得(q-1)Sn=nqn-1-q1-q2-…-qn-1
=nqn-=.
于是,Sn=.
若q=1,则Sn=1+2+3+…+n=.
综上,Sn=
22.设F1、F2为椭圆+=1的两个焦点,P为椭圆上一点,已知P、F1、F2是一个直角三角形的三个顶点,且PF1>PF2,求的值.
23.已知函数f(x)=-x2+2ax+1-a在x∈[0,1]上有最大值2,求a的值.
解 函数f(x)=-x2+2ax+1-a
=-(x-a)2+a2-a+1,
对称轴方程为x=a.
(1)当a<0时,f(x)max=f(0)=1-a,
∴1-a=2,∴a=-1.
(2)当0≤a≤1时,f(x)max=f(a)=a2-a+1,
∴a2-a+1=2,∴a2-a-1=0,
∴a=(舍).
(3)当a>1时,f(x)max=f(1)=a,∴a=2.
综上可知,a=-1或a=2.
24.设集合A={x∈R|x2+4x=0},B={x∈R|x2+2(a+1)x+a2-1=0,a∈R},若B⊆A,求实数a的值.
解 ∵A={0,-4},B⊆A,于是可分为以下几种情况.
(1)当A=B时,B={0,-4},
∴由根与系数的关系,得解得a=1.
(2)当BA时,又可分为两种情况.
①当B≠∅时,即B={0}或B={-4},
当x=0时,有a=±1;
当x=-4时,有a=7或a=1.
又由Δ=4(a+1)2-4(a2-1)=0,
解得a=-1,此时B={0}满足条件;
②当B=∅时,Δ=4(a+1)2-4(a2-1)<0,
解得a<-1.
综合(1)(2)知,所求实数a的取值为a≤-1或a=1.
25.f(x)=x3-x,x1,x2∈[-1,1]时,求证:|f(x1)-f(x2)|≤.