2018届二轮复习空间几何体的三视图、表面积与体积课件理（全国通用）

2018届二轮复习空间几何体的三视图、表面积与体积课件理（全国通用）

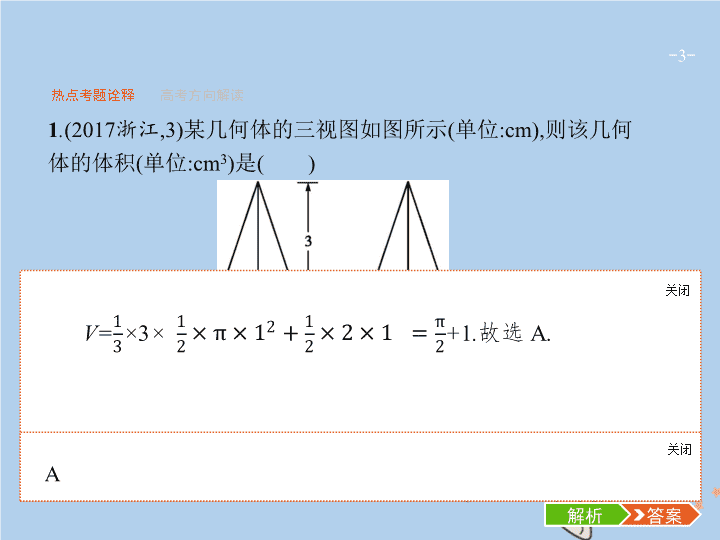
专题五　立体几何与空间向量 第 1 讲　空间几何体的三视图、表面积与体积 - 3 - 热点考题诠释 高考方向解读 1 . (2017 浙江 ,3) 某几何体的三视图如图所示 ( 单位 :cm), 则该几何体的体积 ( 单位 :cm 3 ) 是 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 4 - 热点考题诠释 高考方向解读 2 . (2017 全国 3, 理 8) 已知圆柱的高为 1, 它的两个底面的圆周在直径为 2 的同一个球的球面上 , 则该圆柱的体积为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 5 - 热点考题诠释 高考方向解读 3 . (2017 北京 , 理 7) 某四棱锥的三视图如图所示 , 则该四棱锥的最长棱的长度为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 6 - 热点考题诠释 高考方向解读 4 . (2017 全国 1, 文 16) 已知三棱锥 S -ABC 的所有顶点都在球 O 的球面上 , SC 是球 O 的直径 , 若平面 SCA ⊥ 平面 SCB , SA=AC , SB=BC , 三棱锥 S -ABC 的体积为 9, 则球 O 的表面积为 　　　　　 . 答案 解析 解析 关闭 答案 解析 关闭 - 7 - 热点考题诠释 高考方向解读 5 . (2017 全国 1, 理 16) 如图 , 圆形纸片的圆心为 O , 半径为 5 cm, 该纸片上的等边三角形 ABC 的中心为 O.D , E , F 为圆 O 上的点 , △ DBC , △ ECA , △ FAB 分别是以 BC , CA , AB 为底边的等腰三角形 , 沿虚线剪开后 , 分别以 BC , CA , AB 为折痕折起 △ DBC , △ ECA , △ FAB , 使得 D , E , F 重合 , 得到三棱锥 . 当 △ ABC 的边长变化时 , 所得三棱锥体积 ( 单位 :cm 3 ) 的最大值为 　　　　　　 .   - 8 - 热点考题诠释 高考方向解读 - 9 - 热点考题诠释 高考方向解读 通过对近几年高考试题的分析可看出 , 空间几何体的命题形式比较稳定 , 多为选择题或填空题 , 有时也出现在解答题的某一问中 , 题目难度常为中低档题 . 考查的重点是直观图、三视图、面积与体积等知识 , 此类问题多为考查三视图的还原问题 , 且常与空间几何体的表面积、体积等问题交汇 , 是每年必考的内容 . 对空间几何体的三视图的考查目标是考查考生的空间想象能力 ; 对表面积和体积的考查 , 常见形式为蕴涵在两个几何体的 “ 切 ” 或 “ 接 ” 形态中 , 或以三视图为载体进行综合考查 , 此内容还要注意强化几何体的核心 —— 截面以及补形、切割等数学思想方法的训练 . 考向预测 : 浙江卷本部分内容主要考查通过三视图求体积和表面积 , 以选择题或者填空题形式出现 , 难度不大 . - 10 - 命题热点一 命题热点二 命题热点三 例 1 (1) 一个四面体的顶点在空间直角坐标系 O-xyz 中的坐标分别是 (1,0,1),(1,1,0),(0,1,1),(0,0,0), 画该四面体三视图中的正视图时 , 以 zOx 平面为投影面 , 则得到正视图可以为 ( 　　 ) (2) 已知某几何体的正 ( 主 ) 视图与侧 ( 左 ) 视图都是直角边长为 1 的等腰直角三角形 , 且体积为 , 则该几何体的俯视图可以是 ( 　　 ) - 11 - 命题热点一 命题热点二 命题热点三 答案 : (1)A 　 (2)B - 12 - 命题热点一 命题热点二 命题热点三 规律方法 1 . 三视图中的正 ( 主 ) 视图、侧 ( 左 ) 视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线围成的平面图形 , 反映了一个几何体各个侧面的特点 . 正 ( 主 ) 视图反映物体的主要形状特征 , 是三视图中最重要的视图 ; 俯视图要和正 ( 主 ) 视图对正 , 画在正 ( 主 ) 视图的正下方 ; 侧 ( 左 ) 视图要画在正 ( 主 ) 视图的正右方 , 高度要与正 ( 主 ) 视图平齐 . 2 . 要注意在画三视图时 , 能看到的轮廓线画成实线 , 看不到的轮廓线画成虚线 . - 13 - 命题热点一 命题热点二 命题热点三 迁移训练 1 　 如图 , 在三棱锥 A-BCD 中 , 侧面 ABD ⊥ 底面 BCD , BC ⊥ CD , AB=AD= 4, BC= 6, BD= 4 , 该三棱锥三视图的正视图为 ( 　　 )   答案 解析 解析 关闭 答案 解析 关闭 - 14 - 命题热点一 命题热点二 命题热点三 迁移训练 2 　 将一个长方体截掉一个小长方体 , 所得几何体的俯视图与侧视图如图所示 , 则该几何体的正视图为 ( 　　 )   答案 解析 解析 关闭 答案 解析 关闭 - 15 - 命题热点一 命题热点二 命题热点三 例 2 (1) 某几何体的三视图如图所示 , 则该几何体的体积为 　　　　　 , 表面积为 　　　　　 .   - 16 - 命题热点一 命题热点二 命题热点三 (2) 已知四棱锥的正视图与俯视图如图所示 , 该四棱锥的体积为 24, 则四棱锥的侧视图面积为 　　　　　 , 四棱锥的表面积为 　　　　　 .   - 17 - 命题热点一 命题热点二 命题热点三 - 18 - 命题热点一 命题热点二 命题热点三 - 19 - 命题热点一 命题热点二 命题热点三 规律方法 1 . 求解几何体的表面积时要注意 S 表 =S 侧 +S 底 . 2 . 求几何体的体积问题 , 可以多角度、多方位地考虑 . 对于规则的几何体的体积 , 如求三棱锥的体积 , 采用等体积转化是常用的方法 , 转化的原则是其高与底面积易求 ; 对于不规则几何体的体积常用割补法求解 , 即将不规则几何体转化为规则几何体 , 以易于求解 . 3 . 对于给出几何体的三视图 , 求其体积或表面积的题目关键在于要还原出空间几何体 , 并能根据三视图的有关数据和形状推断出空间几何体的线面关系及相关数据 , 体积或表面积的求解套用对应公式即可 . - 20 - 命题热点一 命题热点二 命题热点三 迁移训练 3 　 《九章算术》卷五商功中有如下问题 : 今有刍甍 , 下广三丈 , 袤四丈 , 上袤二丈 , 无广 , 高一丈 , 问积几何 . 刍甍 : 底面为矩形的屋脊状的几何体 ( 网格纸中粗线部分为其三视图 , 设网格纸上每个小正方形的边长为 1 丈 ), 则该刍甍的体积为 ( 　　 )   A.4 立方丈 B.5 立方丈 C.6 立方丈 D.12 立方丈 答案 解析 解析 关闭 由已知可将刍甍切割成一个三棱柱和一个四棱锥 , 三棱柱的体积为 3 立方丈 , 四棱锥的体积为 2 立方丈 , 则刍甍的体积为 5 立方丈 . 故选 B . 答案 解析 关闭 B - 21 - 命题热点一 命题热点二 命题热点三 迁移训练 4 　 如果一个几何体的三视图如图所示 , 那么这个几何体的表面积是 ( 　　 )   答案 解析 解析 关闭 答案 解析 关闭 - 22 - 命题热点一 命题热点二 命题热点三 例 3 (1) 如图 , 在圆柱 O 1 O 2 内有一个球 O , 该球与圆柱的上、下底面及母线均相切 . 记圆柱 O 1 O 2 的体积为 V 1 , 球 O 的体积为 V 2 , 则 的值是 　　　　　 .   (2) 已知矩形 ABCD 的面积为 8, 当矩形周长最小时 , 沿对角线 AC 把 △ ACD 折起 , 则三棱锥 D-ABC 的外接球的体积为 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 23 - 命题热点一 命题热点二 命题热点三 规律方法 1 . 涉及球与棱柱、棱锥的切、接问题时 , 一般过球心及多面体中的特殊点 ( 一般为接、切点 ) 或线作截面 , 把空间问题转化为平面问题 , 再利用平面几何知识寻找几何体中元素间的关系 , 或只画内切、外接的几何体的直观图 , 确定球心的位置 , 弄清球的半径 ( 直径 ) 与该几何体已知量的关系 , 列方程 ( 组 ) 求解 . 2 . 若球面上四点 P , A , B , C 构成的三条线段 PA , PB , PC 两两互相垂直 , 且 PA=a , PB=b , PC=c , 一般把有关元素 “ 补形 ” 成为一个球内接长方体 , 利用 4 R 2 =a 2 +b 2 +c 2 求解 . - 24 - 命题热点一 命题热点二 命题热点三 迁移训练 5 　 已知三棱锥 S-ABC 所有顶点都在球 O 的球面上 , 且 SC ⊥ 平面 ABC , 若 SC=AB=AC= 1, ∠ BAC= 120 ° , 则球 O 的表面积为 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭 - 25 - 命题热点一 命题热点二 命题热点三 迁移训练 6 　 已知从点 P 出发的三条射线 PA , PB , PC 两两成 60 ° 角 , 且分别与球 O 相切于 A , B , C 三点 . 若球 O 的体积为 36π, 则 O , P 两点间的距离为 ( 　　 )   答案 解析 解析 关闭 答案 解析 关闭 - 26 - 易错点一 易错点二 简单几何体的三视图的识图应搞清正视、侧视、俯视的方向 , 遵循 “ 长对正 , 高平齐 , 宽相等 ” 的原则 , 还要注意几何体中与投影垂直或平行的线段及面的位置关系及实线和虚线的区别 , 实线是能在投影平面上看得见的 , 而虚线在投影图中看不到 , 要善于利用构造正方体、补形等方法探求不易直接观察的三视图 . - 27 - 易错点一 易错点二 例 1 一个几何体的三视图如下图所示 , 正视图与侧视图为全等的矩形 , 俯视图为正方形 , 则该几何体的表面积为 　　　　　 , 体积为 　　　　　 .   - 28 - 易错点一 易错点二 - 29 - 易错点一 易错点二 点评 本题根据三视图中的外围轮廓和内部虚线可知是长方体中挖去一个四棱锥的问题 . 虚线极具干扰性 , 导致判断不清 . - 30 - 易错点一 易错点二 求解组合体的表面积时 , 认真观察组合体的几何特征非常关键 , 特别是分析清楚组合体是由哪几个几何体拼接或挖空而成的 , 它的表面由哪些几何图形组成 , 特别注意不要丢掉底面或者重叠的部分 , 不要计算两次等细节 . - 31 - 易错点一 易错点二 例 2 某几何体的三视图如图所示 , 其表面积为 　 .   - 32 - 易错点一 易错点二 解析 : 由三视图可知 : 此几何体是由上、下两部分组成的 , 上面是一个横放的半圆柱 , 下面是一个四棱锥 , 点评 本题根据三视图可知是一个组合体 , 上面的半圆柱和下面的四棱锥有面积重合部分不用计入表面积 , 计算过程中注意确认每个表面的图形和表面积的计算方法 , 做到不重不漏 . - 33 - 1 2 3 4 5 1 . 某多面体的三视图如图所示 , 其中正视图和左视图都由正方形和等腰直角三角形组成 , 正方形的边长为 2, 俯视图为等腰直角三角形 , 该多面体的各个面中有若干个是梯形 , 这些梯形的面积之和为 ( 　　 ) A . 10 B . 12 C . 14 D . 16 答案 解析 解析 关闭 答案 解析 关闭 - 34 - 1 2 3 4 5 2 . 如图 (1), 把棱长为 1 的正方体沿平面 AB 1 D 1 和平面 A 1 BC 1 截去部分后 , 得到如图 (2) 所示几何体 , 该几何体的体积为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 35 - 1 2 3 4 5 3 . 已知棱长为 2 的正方体 ABCD-A 1 B 1 C 1 D 1 , 一球与该正方体的各个面相切 , 则平面 ACB 1 截此球所得的截面的面积为 ( 　　 ) 答案 解析 解析 关闭 答案 解析 关闭 - 36 - 1 2 3 4 5 4 . 某几何体的三视图如图所示 ( 单位 :cm), 则该几何体的表面积是 　　　　　 cm 2 , 体积是 　　　　　 cm 3 .   答案 解析 解析 关闭 答案 解析 关闭 - 37 - 1 2 3 4 5 5 . 已知一个正方体的所有顶点在一个球面上 , 若这个正方体的表面积为 18, 则这个球的体积为 　　　　　 .   答案 解析 解析 关闭 答案 解析 关闭