高中数学选修2-1公开课课件双曲线的定义及其标准方程

高中数学选修2-1公开课课件双曲线的定义及其标准方程

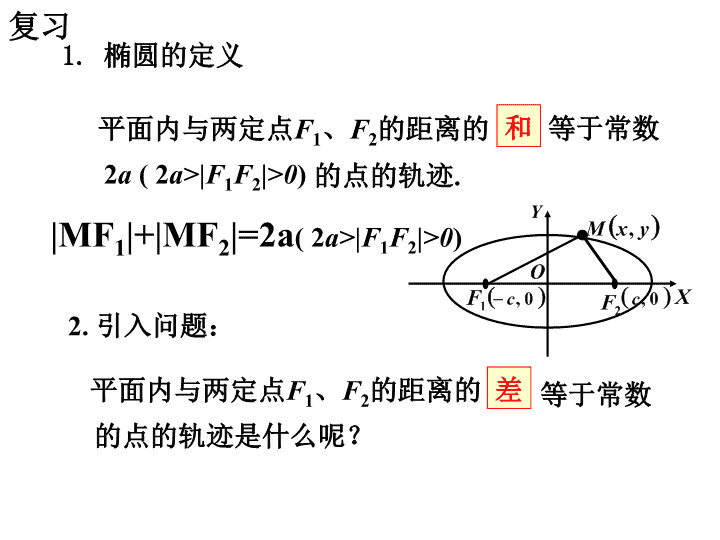
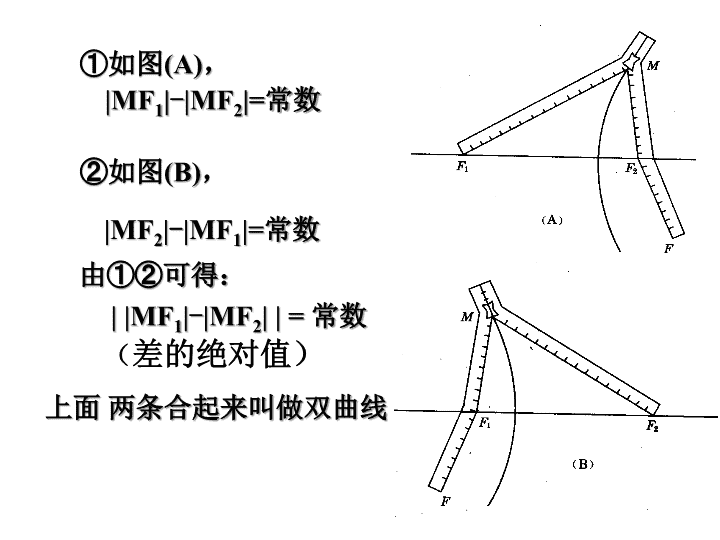
双曲线及其标准方程 1. 椭圆的定义 和 等于常数 2 a ( 2 a>|F 1 F 2 | >0 ) 的点的轨迹 . 平面内与两定点 F 1 、 F 2 的距离的 2. 引入问题： 差 等于常数 的点的轨迹是什么呢？ 平面内与两定点 F 1 、 F 2 的距离的 复习 |MF 1 |+|MF 2 |=2a ( 2 a>|F 1 F 2 | >0 ) ① 如图 (A) ， |MF 1 | - |MF 2 |= 常数 ② 如图 (B) ， 上面 两条合起来叫做双曲线 由①②可得： | |MF 1 | - |MF 2 | | = 常数 （ 差的绝对值） |MF 2 | - |MF 1 |= 常数 双曲线在生活中 ☆ .☆ ① 两个定点 F 1 、 F 2 —— 双曲线的 焦点 ; ② |F 1 F 2 |=2 c —— 焦距 . （ 1 ） 2a< |F 1 F 2| ； o F 2 F 1 M 平面内 与两个定点 F 1 ， F 2 的距离的差 的绝对值等于常数（小于 ︱F 1 F 2 ︱) 的点的轨迹叫做双曲线 . （ 2 ） 2a >0 ； 双曲线定义 思考： （ 1 ）若 2a= |F 1 F 2| , 则轨迹是？ （ 2 ）若 2a> |F 1 F 2| , 则轨迹是？ 说明 （ 3 ）若 2a=0, 则轨迹是？ | |MF 1 | - |MF 2 | | = 2a ( 1 ) 两条射线 ( 2 ) 不表示任何轨迹 (3) 线段 F 1 F 2 的垂直平分线 如何建立适当的直角坐标系？ 原则：尽可能使方程的形式简单、运算简单； ( 一般利用对称轴或已有的互相垂直的线段所在的直线作为坐标轴 .) ♦ 探讨建立平面直角坐标系的方案 O x y O x y O x y 方案一 O x y ( 对称、“简洁” ) O x y 方案二 F 2 F 1 M x O y 求曲线方程的步骤： 双曲线的标准方程 1. 建系 . 以 F 1, F 2 所在的直线为 x 轴，线段 F 1 F 2 的中点为原点建立直角坐标系 2. 设点． 设 M （ x , y ） , 则 F 1 (-c,0),F 2 (c,0) 3. 列式 |MF 1 | - |MF 2 |=±2a 4. 化简 此即为焦点在 x 轴上的双曲线的标准方程 F 2 F 1 M x O y O M F 2 F 1 x y 若建系时 , 焦点在 y 轴上呢 ? 看 前的系数，哪一个为正，则在哪一个轴上 2 、双曲线的标准方程与椭圆的标准方程有何区别与联系 ? 1 、如何判断双曲线的焦点在哪个轴上？ 问题 双曲线定义 双曲线图象 标准方程 焦点 a . b . c 的关系 | |MF 1 | - |MF 2 | | =2 a （０ < 2 a <|F 1 F 2 | ） F ( ±c, 0) 　 F(0, ± c) 定 义 方 程 焦 点 a.b.c 的关系 F （ ±c ， 0 ） F （ ±c ， 0 ） a>0 ， b>0 ，但 a 不一定大于 b ， c 2 =a 2 +b 2 a>b>0 ， a 2 =b 2 +c 2 双曲线与椭圆之间的区别与联系 ||MF 1 | － |MF 2 ||=2a |MF 1 |+|MF 2 |=2a 椭 圆 双曲线 F （ 0 ， ±c ） F （ 0 ， ±c ） 1. 过双曲线 的焦点且垂直 x 轴的弦的长度 为 . 2 . y 2 -2 x 2 =1 的焦点为 、焦距是 . 练习巩固 : 3. 方程 (2+  ) x 2 +(1+  ) y 2 =1 表示双曲线的充要条件 是 . -2<<-1 方程表示的曲线是双曲线 方程表示的曲线是双曲线的右支 方程表示的曲线是 x 轴上分别以 F 1 和 F 2 为端点， 指向 x 轴的负半轴和正半轴的两条射线。 练习巩固 : 例 2 题型二　利用双曲线的定义求轨迹问题 动圆 M 与圆 C 1 ： ( x ＋ 3) 2 ＋ y 2 ＝ 9 外切，且与圆 C 2 ： ( x － 3) 2 ＋ y 2 ＝ 1 内切，求动圆圆心 M 的轨迹方程． 【 名师点评 】 　利用定义法求双曲线的标准方程，首先找出两个定点 ( 即双曲线的两个焦点 ) ；然后再根据条件寻找动点到两个定点的距离的差 ( 或差的绝对值 ) 是否为常数，这样确定 c 和 a 的值，再由 c 2 ＝ a 2 ＋ b 2 求 b 2 ，进而求双曲线的方程． 课本例 2 使 A 、 B 两点在 x 轴上，并且点 O 与线段 AB 的中点重合 解 : 由声速及在 A 地听到炮弹爆炸声比在 B 地晚 2 s , 可知 A 地与爆炸点的距离比 B 地与爆炸点的距离远 680 m . 因为 |AB|>680 m , 所以爆炸点的轨迹是以 A 、 B 为焦点的双曲线在靠近 B 处的一支上 . 例 3 .( 课本第 54 页例 ) 已知 A,B 两地相距 800 m , 在 A 地听到炮弹爆炸声比在 B 地晚 2 s , 且声速为 340 m / s , 求炮弹爆炸点的轨迹方程 . 如图所示，建立直角坐标系 x O y , 设爆炸点 P 的坐标为 ( x , y ) ，则 即 2 a =680 ， a =340 x y o P B A 因此炮弹爆炸点的轨迹方程为 答 : 再增设一个观测点 C ，利用 B 、 C （或 A 、 C ）两处测得的爆炸声的时间差，可以求出另一个双曲线的方程，解这两个方程组成的方程组，就能确定爆炸点的准确位置 . 这是双曲线的一个重要应用 . 例 2 : 如果方程 表示双曲线，求 m 的取值范围 . 解 : 方程 可以表示哪些曲线？ _____________. 思考： 例 3 【 名师点评 】 　双曲线的定义是解决与双曲线有关的问题的主要依据，在应用时，一是注意条件 || PF 1 | － | PF 2 || ＝ 2 a (0<2 a <| F 1 F 2 |) 的使用，二是注意与三角形知识相结合，经常利用正、余弦定理，同时要注意整体运算思想的应用． 跟踪训练 方法感悟 1 ．对双曲线定义的理解 双曲线定义中 || PF 1 | － | PF 2 || ＝ 2 a (2 a <| F 1 F 2 |) ，不要漏了绝对值符号，当 2 a ＝ | F 1 F 2 | 时表示两条射线． 解题时，也要注意 “ 绝对值 ” 这一个条件，若去掉定义中的绝对值则轨迹仅表示双曲线的一支． 2 ．双曲线方程的求法 求双曲线的标准方程包括 “ 定位 ” 和 “ 定量 ” ． “ 定位 ” 是指除了中心在原点之外，判断焦点在哪个坐标轴上，以便使方程的右边为 1 时，确定方程的左边哪一项为正，哪一项为负， “ 定量 ” 是指确定 a 2 ， b 2 的值，即根据条件列出关于 a 2 和 b 2 的方程组，解得 a 2 和 b 2 的具体数值后，再按位置特征写出标准方程． 精彩推荐典例展示 易错警示 双曲线定义运用中的误区 例 4 【 常见错误 】 　 (1) 利用双曲线定义 || PF 1 | － | PF 2 || ＝ 8 求 | PF 2 | 时，易忽略绝对值号，而错选 A. (2) 根据双曲线的定义可得到答案 C ，但由于双曲线上的点到双曲线焦点的最小距离是 c － a ＝ 6 － 4 ＝ 2 ，而 | PF 2 | ＝ 1 ＜ 2 ，不合题意，所以应该舍去，造成错误的原因是忽略双曲线的相关性质，没有检验 | PF 1 | ＋ | PF 2 | ＝ 10 ＜ | F 1 F 2 | 造成的． 【 解析 】 　双曲线的实轴长为 8 ，由双曲线的定义得 || PF 1 | － | PF 2 || ＝ 8 ， 所以 |9 － | PF 2 || ＝ 8 ， 所以 | PF 2 | ＝ 1 或 17. 因为 | F 1 F 2 | ＝ 12 ，当 | PF 2 | ＝ 1 时， | PF 1 | ＋ | PF 2 | ＝ 10 ＜ | F 1 F 2 | ， 不符合公理 “ 两点之间线段最短 ” ，应舍去． 所以 | PF 2 | ＝ 17. 【 答案 】 　 B 【 失误防范 】 　运用双曲线的定义解决相关问题时， (1) 不能忽略 “ 绝对值 ” 号，以免造成漏解， (2) 求出解后，要注意检验根的合理性，以免出现增根． 跟踪训练 **** * * 小结 * * **** 感谢您的聆听！ THANKS FOR YOUR KIND ATTENTION ！ LOVELL