2019-2020学年安徽省滁州市定远县育才学校高二（普通班）上学期期末考试数学（理）试题 Word版

2019-2020学年安徽省滁州市定远县育才学校高二（普通班）上学期期末考试数学（理）试题 Word版

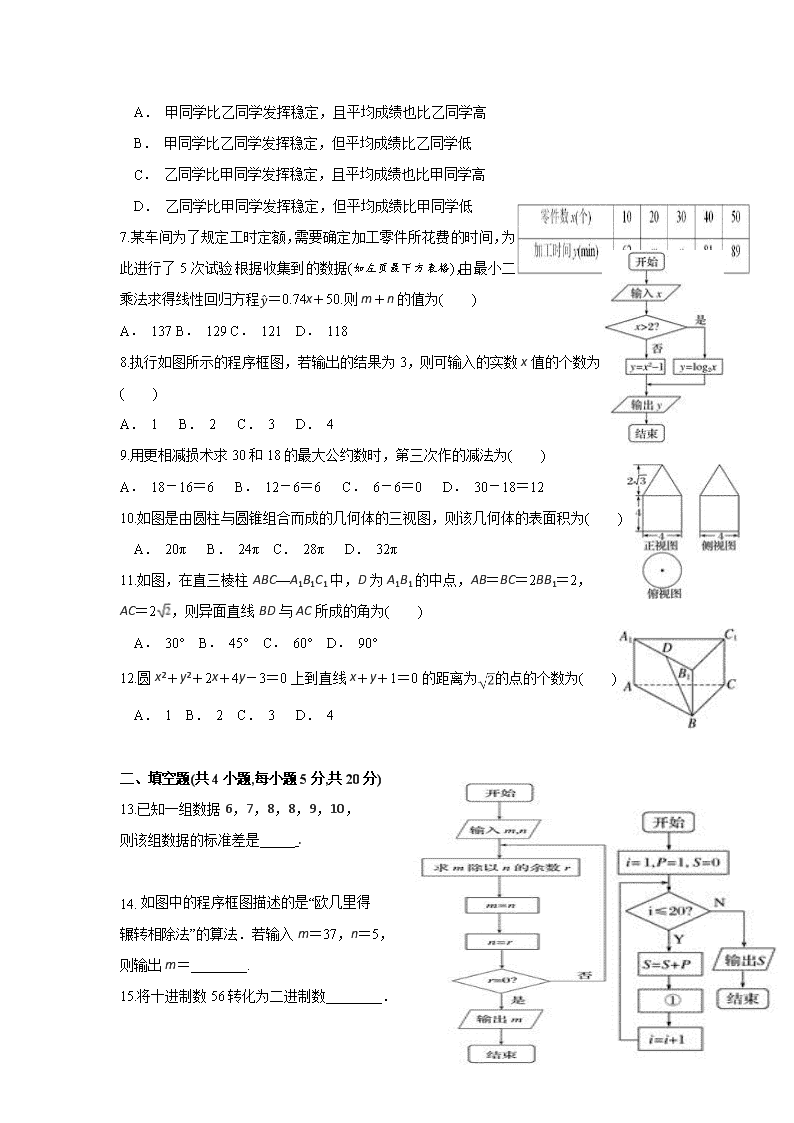
安徽省滁州市定远县育才学校育才学校2019--2020学年度第一学期期末考试 高二普通班（理科）数学 ‎ ‎ 考试时间:120分钟　满分:150分 ‎ 一、选择题(共12小题，每小题5分，共60分) ‎ ‎1.要完成下列两项调查：‎ ‎①从某社区125户高收入家庭，280户中等收入家庭，95户低收入家庭中选出100户调查社会购买力的某项指标；②从某中学的15名艺术特长生中选出3人调查学习负担情况.宜采用的抽样方法依次为(　　)‎ A． ①简单随机抽样；②系统抽样 B． ①分层抽样；②简单随机抽样 C． ①系统抽样；②分层抽样 D． ①②都用分层抽样 ‎2.某中学有高中生3 500人，初中生1 500人，为了解学生的学习情况，用分层抽样的方法从该校学生中抽取一个容量为n的样本，已知从高中生中抽取70人，则n为(　　)‎ A． 100 B． ‎150 C． 200 D． 250‎ ‎3.现有60瓶牛奶，编号为1至60，若从中抽取6瓶检验，用系统抽样方法确定所抽取的编号可能为(　　)‎ A． 3,13,23,33,43,53 B． 2,14,26,38,42,‎56 C． 5,8,31,36,48,54 D． 5,10,15,20,25,30‎ ‎4.某中学举办电脑知识竞赛，满分为100分，80分以上为优秀(含80分)，现将高一两个班参赛学生的成绩进行整理后分成五组：第一组[50,60)，第二组[60,70)，第三组[70,80)，第四组[80,90)，第五组[90,100]，其中第一、三、四、五小组的频率分别为0.30,0.15,0.10,0.05，而第二小组的频数是40，则参赛的人数以及成绩优秀的概率分别是(　　)‎ A． 50,0.15 B． 50,‎0.75 C． 100,0.15 D． 100,0.75‎ ‎5.如图所示的茎叶图记录了甲、乙两组各五名学生在一次英语听力测试中的成绩(单位：分).已知甲组数据的中位数为106，乙组数据的平均数为105.4，则x，y的值分别为(　　)‎ A． 5,7 B． 6,‎8 C． 6,9 D． 8,8‎ ‎6.甲、乙两名同学12次考试中数学成绩的茎叶图如图所示，则下列说法正确的是(　　)‎ A． 甲同学比乙同学发挥稳定，且平均成绩也比乙同学高 B． 甲同学比乙同学发挥稳定，但平均成绩比乙同学低 C． 乙同学比甲同学发挥稳定，且平均成绩也比甲同学高 D． 乙同学比甲同学发挥稳定，但平均成绩比甲同学低 ‎7.某车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了5次试验．根据收集到的数据(如左页最下方表格)，由最小二乘法求得线性回归方程＝0.74x＋50.则m＋n的值为(　　)‎ A． 137 B． ‎129 C． 121 D． 118‎ ‎8.执行如图所示的程序框图，若输出的结果为3，则可输入的实数x值的个数为(　　)‎ A． 1 B． ‎2 C． 3 D． 4‎ ‎9.用更相减损术求30和18的最大公约数时，第三次作的减法为(　　)‎ A． 18－16＝6 B． 12－6＝‎6 C． 6－6＝0 D． 30－18＝12‎ ‎10.如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为(　　)‎ A． 20π B． 24π C． 28π D． 32π ‎11.如图，在直三棱柱ABC—A1B‎1C1中，D为A1B1的中点，AB＝BC＝2BB1＝2，‎ AC＝2，则异面直线BD与AC所成的角为(　　)‎ A． 30° B． 45° C． 60° D． 90°‎ ‎12.圆x2＋y2＋2x＋4y－3＝0上到直线x＋y＋1＝0的距离为的点的个数为(　　)‎ A． 1 B． ‎2 C． 3 D． 4‎ 二、填空题(共4小题,每小题5分,共20分) ‎ ‎13.已知一组数据6，7，8，8，9，10，‎ 则该组数据的标准差是_____ .‎ 14. 如图中的程序框图描述的是“欧几里得 辗转相除法”的算法．若输入m＝37，n＝5，‎ 则输出m＝________.‎ ‎15.将十进制数56转化为二进制数________．‎ ‎16.如图所示程序为求：S＝1＋2＋4＋7＋11‎ ‎＋…的前20项和的流程图，①处应填________.‎ ‎ ‎ ‎ （第14题图） （第16题图）‎ 三、解答题(共6小题,共70分) ‎ ‎17.（本小题10分）‎ 已知直线l：x－2y－5＝0与圆C：x2＋y2＝50.求：‎ ‎(1)交点A，B的坐标；(2)△AOB的面积．‎ 18. ‎（本小题12分）‎ 某良种培育基地正在培育一种小麦新品种A.将其与原有的一个优良品种B进行对照试验．两种小麦各种植了25亩，所得亩产数据(单位：千克)如下：‎ 品种A：357,359,367,368,375,388,392,399,400,405,412,414,415,421,‎ ‎423,423,427,430,430,434,443,445,445,451,454‎ 品种B：363,371,374,383,385,386,391,392,394,394,395,397,397,400,‎ ‎401,401,403,406,407,410,412,415,416,422,430‎ ‎(1)完成所附的茎叶图；(2)用茎叶图处理现有的数据，有什么优点？‎ ‎(3)通过观察茎叶图，对品种A与B的亩产量及其稳定性进行比较，写出统计结论．‎ ‎19.（本小题12分）下表是某中学对本校初中二年级女生身高情况进行抽测后所得的部分资料(身高单位：cm，测量时精确到‎1 cm)．已知身高在‎151 cm(含‎151 cm)以下的被测女生共3人.‎ ‎(1)求所有被测女生总数；‎ ‎(2)求身高在‎161 cm(含‎161 cm)以上的被测女生数；‎ ‎(3)完成频率分布直方图．‎ ‎20.（本小题12分）‎ 假设关于某设备的使用年限x(年)和所支出的维修费用y(万元)有如下的统计资料：‎ ‎(1)画出散点图并判断是否线性相关；‎ ‎(2)如果线性相关，求线性回归方程；‎ ‎(3)估计使用年限为10年时，维修费用是多少？‎ ‎21.（本小题12分）‎ 现有某城市100户居民的月平均用电量(单位：度)的数据，根据这些数据，以[160,180)，[180,200)，[200,220)，[220,240)，[240,260)，[260,280)，[280,300]分组的频率分布直方图如图所示.‎ ‎(1)求直方图中x的值；‎ ‎(2)求月平均用电量的众数和中位数；‎ ‎(3)在月平均用电量为[220,240)，[240,260)，[260,280)，[280,300]的四组用户中，用分层抽样的方法抽取11户 居民，则月平均用电量在[220,240)内的用户中应抽取 多少户？‎ ‎22.（本小题12分）‎ 如图所示，在直四棱柱ABCD－A1B‎1C1D1中，DB＝BC，DB⊥AC，点M是棱BB1上一点．‎ ‎(1)求证：B1D1∥平面A1BD；‎ ‎(2)求证：MD⊥AC；‎ ‎(3)试确定点M的位置，使得平面DMC1⊥平面CC1D1D.‎ 参考答案 ‎1.B 2.A 3.A 4.C 5.B 6.C 7.B 8.C 9.B 10.C 11.C 12.C ‎13.5/3‎ ‎14.1‎ ‎15.111 000(2)‎ ‎16.P＝P＋i ‎17.解　(1)解方程组得或所以直线l：x－2y－5＝0与圆x2＋y2＝50的交点是A(－5，－5)，B(7,1)．‎ ‎(2)过圆心O作直线l的垂线，垂足为D，‎ 则圆心O到直线l的距离＝＝.‎ 在Rt△AOD中，＝5，＝＝3.所以＝6.‎ ‎△AOB的面积S△AOB＝×＝×6×＝15.‎ ‎18.(1)‎ ‎(2)由于每个品种的数据都只有25个，样本不大，画茎叶图很方便；此时茎叶图不仅清晰明了的展示了数据的分布情况，便于比较，没有任何信息损失，而且还可以随时记录新的数据．‎ ‎(3)通过观察茎叶图可以看出：①品种A的亩产平均数(或均值)比品种B高；②品种A的亩产标准差(或方差)比品种B大，故品种A的亩产稳定性较差．‎ ‎19.解　(1)∵被测女生中，身高为‎151cm(含‎151cm)以下的共3人，‎ ‎∴第1组和第2组的频率和为0.06，频数为3，‎ ‎∴被测女生数为＝50；‎ ‎(2)∵身高为‎161cm(含‎161cm)以上的女生的数据落在第6、7、8组．‎ 这三组的频率和为0.20＋0.18＋0.06＝0.44，‎ ‎∴人数为50×0.44＝22；‎ ‎(3)要点：横轴：身高/cm；纵轴：频率/组距；‎ 长方形的高的比例：1∶2∶4∶6∶15∶10∶9∶3.‎ ‎20.解　(1)作散点图如下：‎ 由散点图可知是线性相关的.‎ ‎(2)列表如下：‎ 计算得：＝＝＝1.23，‎ 所以＝－＝5－1.23×4＝0.08，‎ 即得线性回归方程为＝1.23x＋0.08.‎ ‎(3)把x＝10代入线性回归方程＝1.23x＋0.08，‎ 得y＝12.38，因此，估计使用10年维修费用是12.38万元.‎ ‎21.解　(1)由(0.002＋0. 009 5＋0.011＋0.012 5＋x＋0.005＋0.002 5)×20＝1得x＝0.007‎ ‎ 5，‎ 故直方图中x的值是0.007 5.‎ ‎(2)月平均用电量的众数为＝230.‎ ‎∵(0.002＋0.009 5＋0.011)×20＝0.45＜0.5，‎ ‎∴月平均用电量的中位数在[220,240)内，设中位数为a，‎ 由(0.002＋0.009 5＋0.011)×20＋0.012 5×(a－220)＝0.5，得a＝224，‎ 即月平均用电量的中位数为224.‎ ‎(3)月平均用电量在[220,240)内的有0.012 5×20×100＝25(户)，月平均用电量在[240,260)内的有0.007 5×20×100＝15(户)，月平均用电量在[260,280)内的有0.005×20×100＝10(户)，月平均用电量在[280,300]内的有0.002 5×20×100＝5 (户)，‎ 抽取比例为＝，‎ ‎∴月平均用电量在[220,240)内的用户中应抽取25×＝5(户).‎ ‎22.(1)证明　由ABCD－A1B‎1C1D1为直四棱柱，得BB1∥DD1且BB1＝DD1，所以BB1D1D是平行四边形，所以B1D1∥BD.而BD⊂平面A1BD，B1D1⊄平面A1BD，‎ 所以B1D1∥平面A1BD.‎ ‎(2)证明　连接B1D，因为BB1⊥平面ABCD，AC⊂平面ABCD，‎ 所以BB1⊥AC，‎ 又因为BD⊥AC，且BD∩BB1＝B，‎ 所以AC⊥平面BB1D，‎ 而MD⊂平面BB1D，所以MD⊥AC.‎ ‎(3)解　当点M为棱BB1的中点时，平面DMC1⊥平面CC1D1D，‎ 取DC的中点N，D‎1C1的中点N1，连接NN1交DC1于O，连接OM，BN.‎ 因为N是DC的中点，BD＝BC，所以BN⊥DC；又因为DC是平面ABCD与平面DCC1D1的交线，而平面ABCD⊥平面DCC1D1，所以BN⊥平面DCC1D1.‎ 又可证得，O是NN1的中点，所以BM∥ON且BM＝ON，即BMON是平行四边形，所以BN∥OM，所以OM⊥平面CC1D1D，因为OM⊂平面DMC1，所以平面DMC1⊥平面CC1D1D.‎